Слайд 2
Знаково - символические учебные
действия:
— кодирование/замещение
(использование знаков и символов как условных заместителей реальных объектов и предметов);
— декодирование/считывание информации;
— умение использовать наглядные модели (схемы, чертежи, планы), отражающие пространственное расположение предметов или отношения между предметами или их частями для решения задач;
— умение строить схемы, модели и т. п.
Слайд 3
В период начального образования
основным показателем развития
знаково
- символических
универсальных учебных действий
становится овладение
моделированием.
Слайд 4
Частным случаем моделирования является
графическое моделирование –
это
перевод текста задачи на математический язык.
Модели задач:
«Блок-схема»,
«графы»,
«схематический чертёж»,
«графическая схема» ,
«схема - отрезок».
Слайд 5
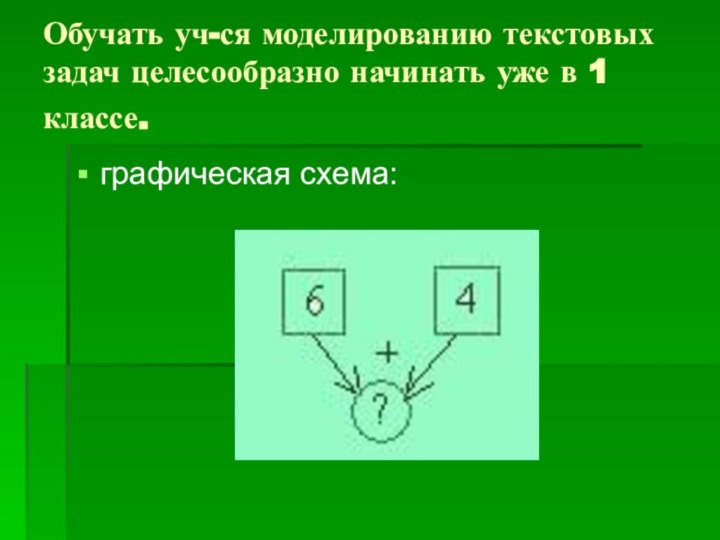
Обучать уч-ся моделированию текстовых задач целесообразно начинать уже
в 1 классе.
графическая схема:
Слайд 6
5 видов графических схем:
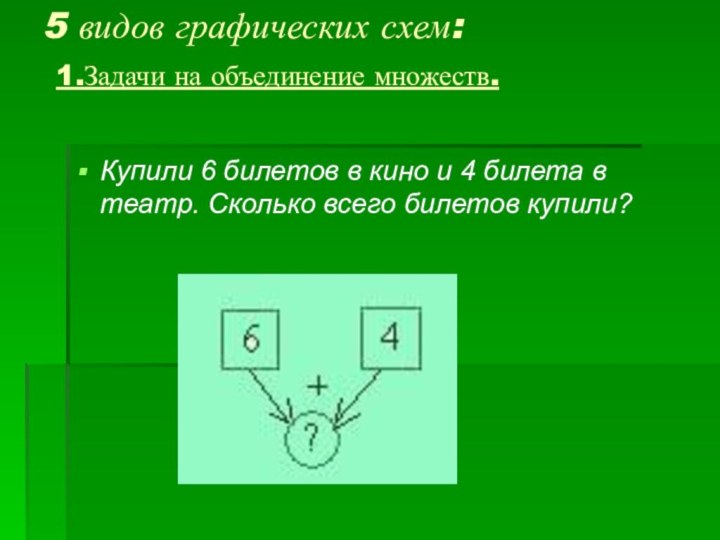
1.Задачи на объединение множеств.
Купили
6 билетов в кино и 4 билета в театр.
Сколько всего билетов купили?
Слайд 7
2.Задачи на удаление части множества.
У Коли 7 книг.3
книги он подарил другу. Сколько книг осталось у Коли?
Слайд 8
3.Задачи на сравнение множеств.
В шкафу 6 кукол,
а машинок 4. На сколько больше кукол, чем машинок
в шкафу?
Слайд 9
4.Задачи на увеличение числа на несколько единиц.
Таня
прочитала 7 страниц , а ее брат на 2
страницы больше. Сколько страниц прочитал брат?
Слайд 10
5.Задачи на уменьшение числа на несколько единиц.
В
саду собрали 5 кг смородины, а малины на 2
кг меньше. Сколько кг малины собрали в саду?
Слайд 11
Правила построения схемы:
Схема составляется не после чтения и
анализа задачи, а параллельно, по мере чтения текста.
Обозначения
данных и искомых лучше сразу разносить: наверху данные, ниже – искомое. Тогда схема визуально отражает структуру задачи: условие с данными и вопрос с искомым.
-Разбор текста выполняется уже по схеме (к тексту обращаются только в случае каких-то неясностей).
-Анализ удобнее выполнять от данных к вопросу.
-Знак действия ставится после расстановки стрелок, а точнее: их направления. После этого записывается решение и ответ. Направления стрелок показывают направление действия, знак действия.
Слайд 12
Алгоритм решения задач:
1.В задаче известно, (неизвестно)…
2.Прочитаю вопрос…
3.Составлю схему…
4.Составлю план решения.
5. Запишу решение.
6. Запишу ответ.
7. Сделаю проверку.
Слайд 13
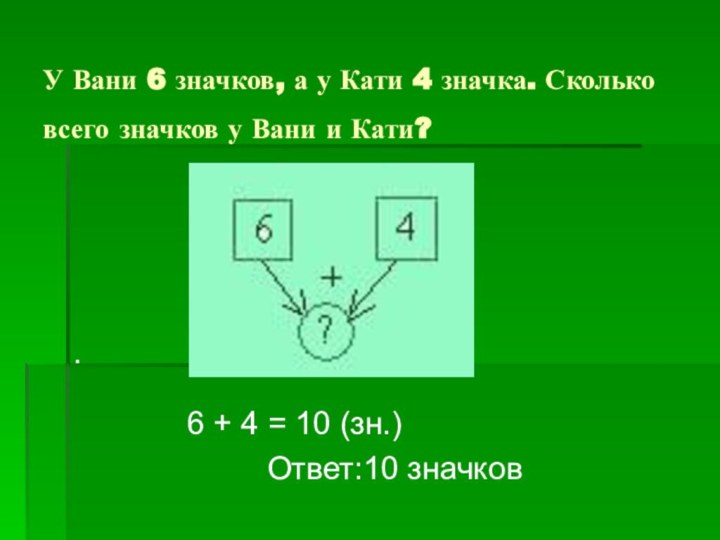
У Вани 6 значков, а у Кати 4
значка. Сколько всего значков у Вани и Кати?
6
Слайд 14
У Вани 6 значков, а у Кати 4
значка. Сколько всего значков у Вани и Кати?
6 4
Слайд 15
У Вани 6 значков, а у Кати 4
значка. Сколько всего значков у Вани и Кати?
6 4
?
Слайд 16
У Вани 6 значков, а у Кати 4
значка. Сколько всего значков у Вани и Кати?
Слайд 17
У Вани 6 значков, а у Кати 4
значка. Сколько всего значков у Вани и Кати?
.
6 + 4 = 10 (зн.)
Ответ:10 значков
Слайд 18
Схемы составных задач:
Саша нашел 7
грибов, а Петя - на 2 гриба больше. Сколько
грибов у Саши и Пети?
Слайд 19
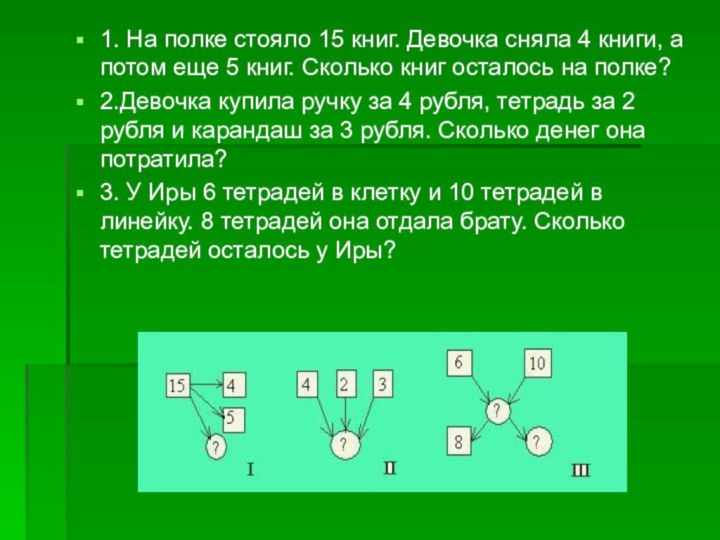
1. На полке стояло 15 книг. Девочка сняла
4 книги, а потом еще 5 книг. Сколько книг
осталось на полке?
2.Девочка купила ручку за 4 рубля, тетрадь за 2 рубля и карандаш за 3 рубля. Сколько денег она потратила?
3. У Иры 6 тетрадей в клетку и 10 тетрадей в линейку. 8 тетрадей она отдала брату. Сколько тетрадей осталось у Иры?
Слайд 20
Более сложные модели задач:
Графы,
Схематический чертёж.
Алгоритм решения
задач с помощью «схематического чертежа» основывается на понимании и
использовании учащимися терминов « целое», «часть», а также определённых правил:
Чтобы найти часть, нужно от целого отнять другую часть.
Чтобы найти целое, нужно сложить части.
Слайд 21
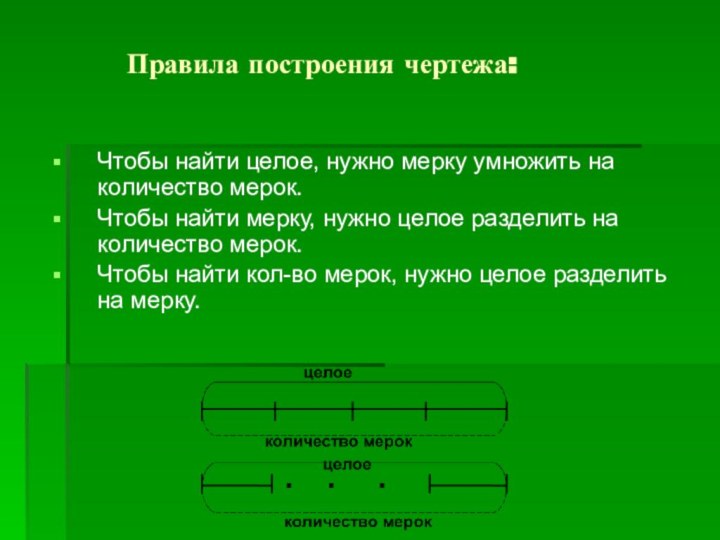
Правила построения чертежа:
Чтобы
найти целое, нужно мерку умножить на количество мерок.
Чтобы найти
мерку, нужно целое разделить на количество мерок.
Чтобы найти кол-во мерок, нужно целое разделить на мерку.
Слайд 22
На каждом уроке рекомендуется использовать следующие упражнения:
Выбор графической
схемы к задаче.
Выбор задачи к схеме.
Заполнение начатой схемы
данными задачи.
Соотнесение схемы и числового выражения.
Нахождение ошибок в заполнении схемы.
Завершение построения схемы.
Слайд 23
В процессе работы с моделями
методист Р.Н. Шишкова
предупреждает о том,
что «построение моделей к решаемым задачам
не должно быть самоцелью, использовать наглядность нужно в разумной мере.
Нежелательно требовать от учащихся вспомогательной модели к каждой решаемой ими задачи.
Учитель не должен превращать построение моделей в дополнительную нагрузку в том случае, если школьник может найти решение, мысленно представив себе задачную ситуацию».