Слайд 2
Задание 11. Умение анализировать информацию, представленную в виде
схем
Пример
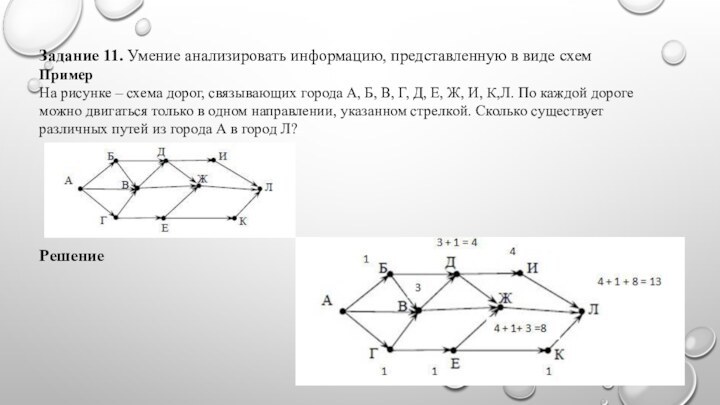
На рисунке – схема дорог, связывающих города А, Б,
В, Г, Д, Е, Ж, И, К,Л. По каждой дороге можно двигаться только в одном направлении, указанном стрелкой. Сколько существует различных путей из города А в город Л?
Решение
Слайд 3
Решение
Цифры у каждой вершины показывают количество дорог, которые

ведут к этой вершине. Подробнее: из А в Б
ведёт одна дорога, пишем 1. Аналогично - из А-Г 1дорога, из А в В ведут 3 дороги, пишем 3. В пункт Д ведут одна дорога из Б + одна дорога из В, но, так как в В можно попасть тремя дорогами, значит, из А в Д можно проехать 1 + 3 = 4 дорогами. Если между пунктами одна дорога, то цифра повторяет предыдущую, если дорог несколько, складываем количество дорог, ведущих в каждый предыдущий пункт. Например, из Д в И ведёт одна дорога, но, так как в Д можно попасть 4 путями, то и в И можно приехать 4 дорогами. В Ж можно попасть из Е (1 дорога), и из В (3 дороги), и из Д (4 дороги), значит, в Ж всего ведут 8 дорог. Продолжаем до пункта Л ( К - 1дорога, Ж – 8 дорог, И - 4 дороги), всего 1 + 4 + 8 = 13 дорог.
Еще один способ решения
Считаем количество путей с конца маршрута – с города Л. Пусть NX – количество различных путей , ведущих в город X, а N – общее количество путей. В Л можно проехать из Ж, И и К, поэтому N = NЛ = NЖ + NИ+ N К (1).
Аналогично
NЖ = NД + NВ + NЕ = (NБ + NВ )+ (1 + NБ + NГ ) + NГ = 4 + 3 + 1 = 8;
NИ = NД = NБ + NВ = 1 + 1 + NБ+ NГ =1+ 1+ 1 + 1 = 4;
NК = NЕ = NГ = 1;
Подставляем значения в формулу (1): N = 8+ 4 + 1 = 13
Ответ: 13
Слайд 4
Рассмотрим еще один пример
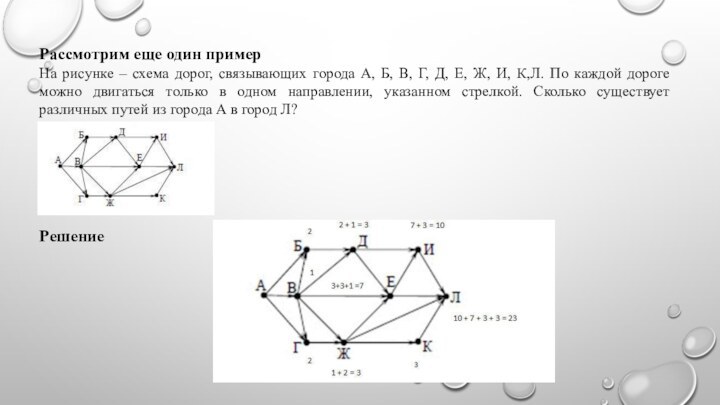
На рисунке – схема дорог,
связывающих города А, Б, В, Г, Д, Е, Ж,
И, К,Л. По каждой дороге можно двигаться только в одном направлении, указанном стрелкой. Сколько существует различных путей из города А в город Л?
Решение
Слайд 5
Решение
Цифры у каждой вершины показывают количество дорог, которые
ведут к этой вершине. Подробнее: из А в В
ведёт одна дорога, пишем 1. Аналогично - из А в Б ведут 2 дороги, из А в Г ведут 2 дороги, пишем 2. В пункт Д ведут одна дорога из Б + одна дорога из В, но, так как в Б можно попасть двумя дорогами, значит, из А в Д можно проехать 1 + 2 = 3 дорогами. Если между пунктами одна дорога, то цифра повторяет предыдущую цифру, если дорог несколько, складываем количество дорог, ведущих в каждый предыдущий пункт. Например, из Ж в К ведёт одна дорога, но, так как в Ж можно попасть 3 путями, то и в К можно приехать 3 дорогами. В Е можно попасть из Д (3 дороги), и из В (1 дорога), и из Ж (3 дороги), значит, в Е всего ведут 7 дорог. Продолжаем до пункта Л (К – 3 дороги, Ж – 3 дороги, И - 10 дорог, Е- 7 дорог), всего 10 +7 +3 + 3 = 23 дороги.
Ответ: 23
Слайд 6
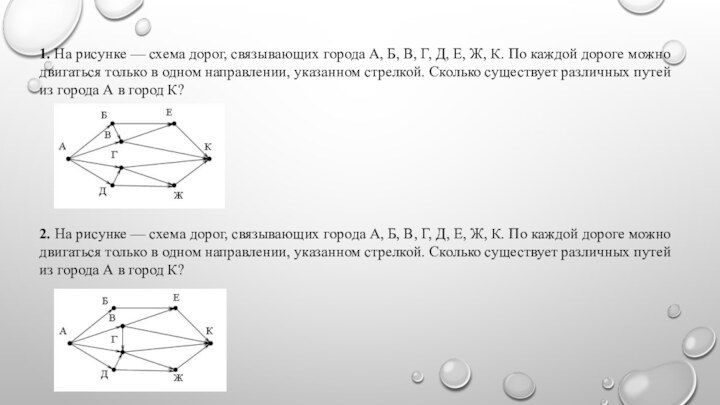
1. На рисунке — схема дорог, связывающих города
А, Б, В, Г, Д, Е, Ж, К. По
каждой дороге можно двигаться только в одном направлении, указанном стрелкой. Сколько существует различных путей из города А в город К?
2. На рисунке — схема дорог, связывающих города А, Б, В, Г, Д, Е, Ж, К. По каждой дороге можно двигаться только в одном направлении, указанном стрелкой. Сколько существует различных путей из города А в город К?
Слайд 7
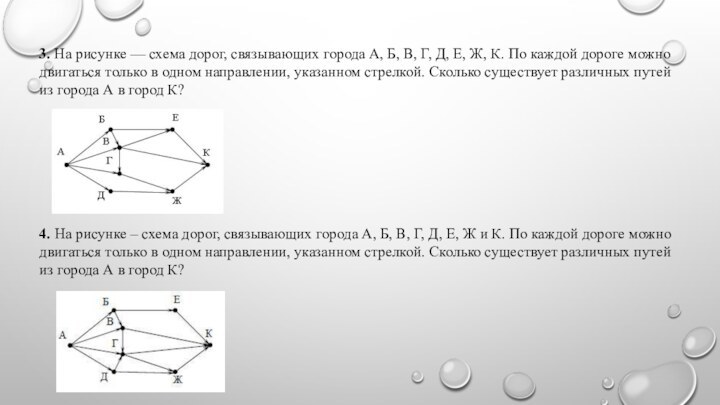
3. На рисунке — схема дорог, связывающих города
А, Б, В, Г, Д, Е, Ж, К. По
каждой дороге можно двигаться только в одном направлении, указанном стрелкой. Сколько существует различных путей из города А в город К?
4. На рисунке – схема дорог, связывающих города А, Б, В, Г, Д, Е, Ж и К. По каждой дороге можно двигаться только в одном направлении, указанном стрелкой. Сколько существует различных путей из города А в город К?
Слайд 8
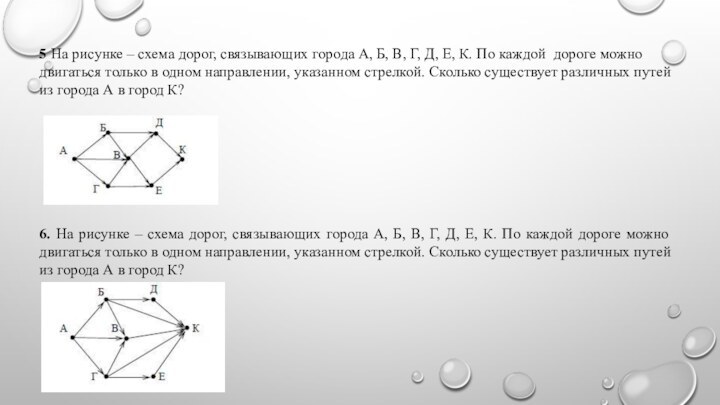
5 На рисунке – схема дорог, связывающих города
А, Б, В, Г, Д, Е, К. По каждой
дороге можно двигаться только в одном направлении, указанном стрелкой. Сколько существует различных путей из города А в город К?
6. На рисунке – схема дорог, связывающих города А, Б, В, Г, Д, Е, К. По каждой дороге можно двигаться только в одном направлении, указанном стрелкой. Сколько существует различных путей из города А в город К?
Слайд 9
Ответы:
1. 10
2. 10
3. 9
4. 12
5. 8
6. 7