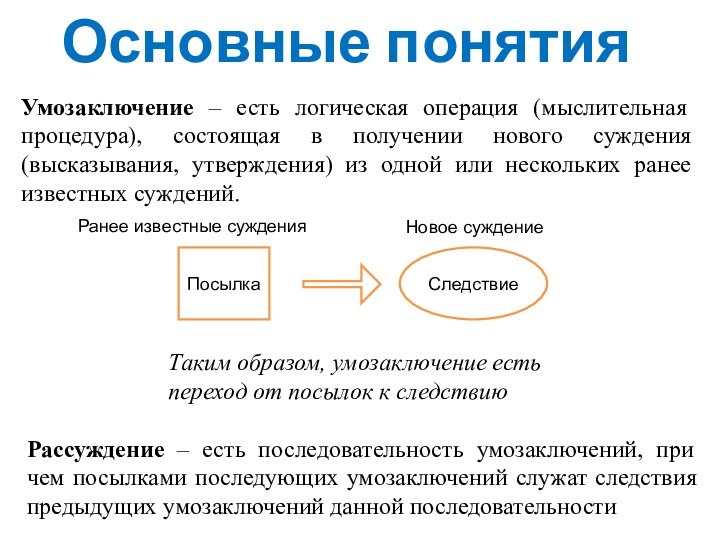
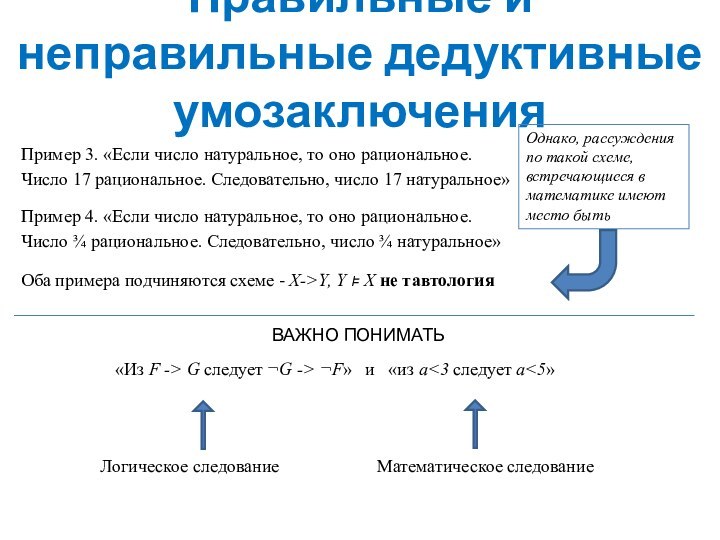
математики»
Доказательство равенства 3=7. «Из чисел 3 и 7
вычитаем одно и то же число 5. Получаем: 3-5=-2, 7-5=2. Возводим числа в квадрат. Результат – 4 и 4, числа равны, значит и 3=7»
Анализ рассуждения
Шаг 1 (вычитание из целых чисел 3 и 7 целого числа 5)
Посылки: «Если a и b – целые числа, то их разность существует» (A -> B), «Числа 3 и 5 – целые» (А).
Заключение: «Разности 3-5 и 7-5 существуют» (B)
Шаг 2 (возведение чисел -2 и 2 в квадрат).
Посылки: «Если число целое, то его квадрат существует и является >0» (A -> B), «Число (-2) – целое» (A). Заключение: «Квадраты чисел (-2) и 2 существуют» (B)
Шаг 3 (заключение о равенстве чисел 3 и 7).
Посылки: «Если целые числа равны, то равны и их квадраты» (A -> B), «Квадраты целых чисел (-2) и 2 = 4» (B).
Заключение: «Равны числа -2 и 2, т.е. их разности, т.е. 3=7» (A)
T
T
F