- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Соотношение между сторонами и углами. Полная версия презентации
Содержание
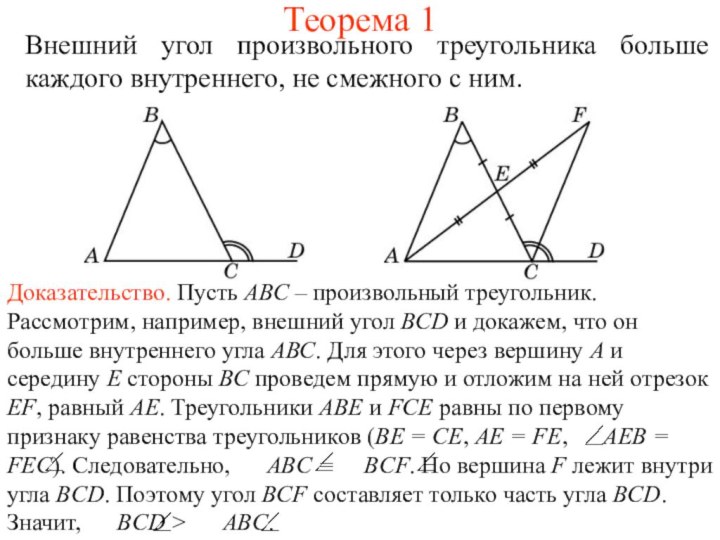
- 2. Теорема 2В произвольном треугольнике против большей стороны лежит больший угол.
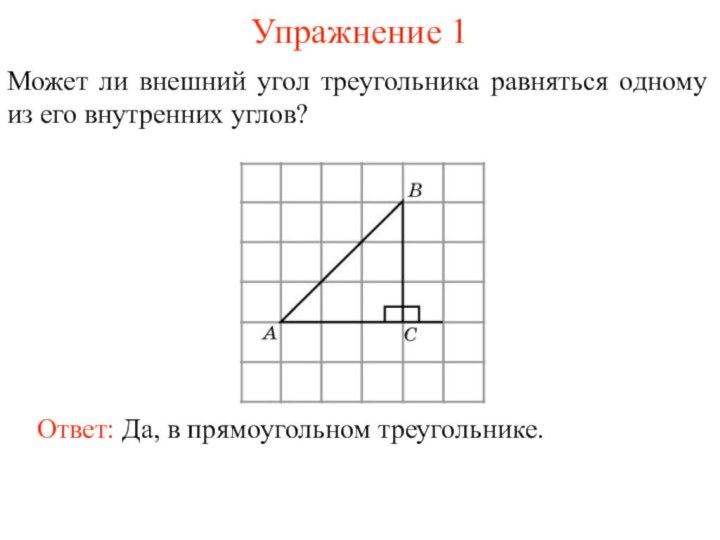
- 3. Упражнение 1Может ли внешний угол треугольника равняться одному из его внутренних углов?
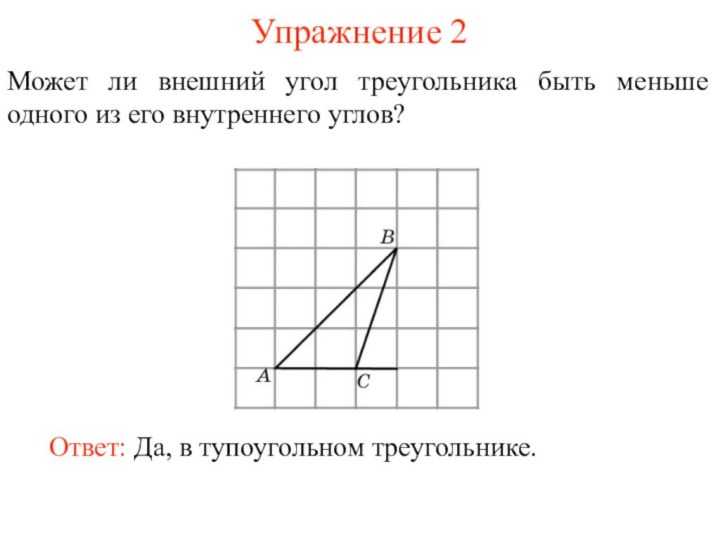
- 4. Упражнение 2Может ли внешний угол треугольника быть меньше одного из его внутреннего углов?
- 5. Упражнение 3Сколько в треугольнике может быть: а) прямых углов; б) тупых углов? Ответ: а), б) Один.
- 6. Упражнение 4Известно, что в треугольнике ABC BC
- 7. Упражнение 5В треугольнике ABC сторона AB наибольшая.
- 8. Упражнение 6Докажите, что в произвольном треугольнике против
- 9. Упражнение 7На рисунке угол 1 меньше угла
- 10. Упражнение 8Ответ: а) BC > AC >
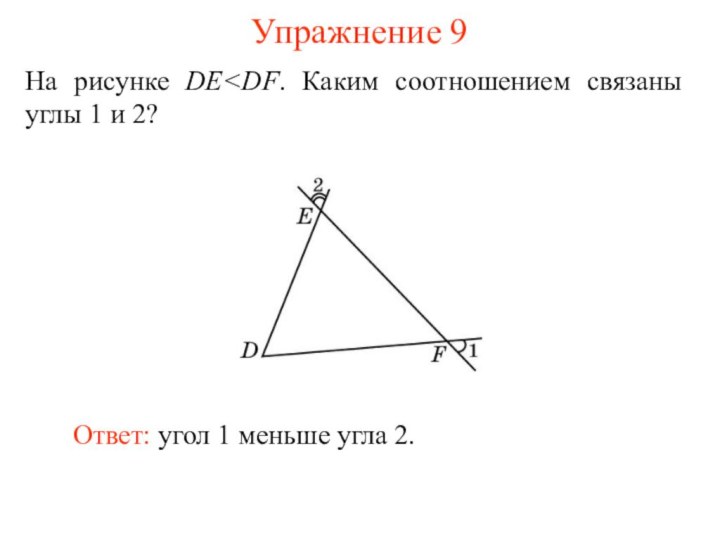
- 11. Упражнение 9На рисунке DE
- 12. Упражнение 10Какой вид имеет треугольник, если: а)
- 13. Упражнение 11На рисунке AB > BC. Докажите, что угол 1 больше угла 2.
- 14. Упражнение 12На рисунке угол 1 больше угла 2. Докажите, что AB > BC.
- 15. Упражнение 13На рисунке угол 1 равен углу
- 16. Упражнение 14На рисунке угол 1 равен углу
- 17. Упражнение 15В выпуклом четырехугольнике ABCD AB =
- 18. Упражнение 16В выпуклом четырехугольнике ABCD AB =
- 19. Упражнение 17В выпуклом четырехугольнике ABCD AB =
- 20. Упражнение 18В выпуклом четырехугольнике ABCD AB =
- 21. Упражнение 19Вершины треугольника ABC соединены отрезками с
- 22. Упражнение 20Вершины треугольника ABC соединены отрезками с
- 23. Упражнение 21Отрезки AE и BD пересекаются в
- 24. Упражнение 22Отрезки AE и BD пересекаются в
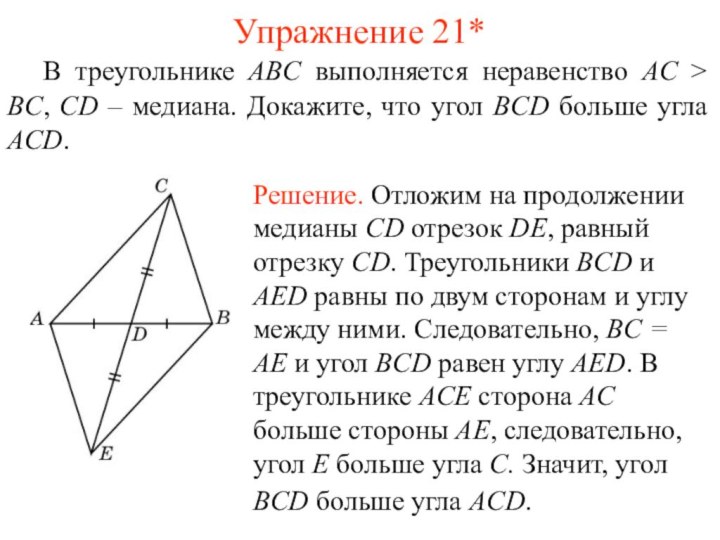
- 25. Упражнение 21* В треугольнике ABC выполняется неравенство AC
- 26. Скачать презентацию
- 27. Похожие презентации













Слайд 5
Упражнение 3
Сколько в треугольнике может быть:
а) прямых
углов;
б) тупых углов?
Ответ: а), б) Один.
Слайд 6
Упражнение 4
Известно, что в треугольнике ABC BC >
AC >AB. Какой из углов больше: а) B или
A; б) C или A; в) B или С?Ответ: а), б) A; в) B.
Слайд 7
Упражнение 5
В треугольнике ABC сторона AB наибольшая. Какие
углы этого треугольника острые? Каким может быть угол C?
Ответ:
Углы A и B острые. Угол C может быть острым, прямым или тупым.
Слайд 8
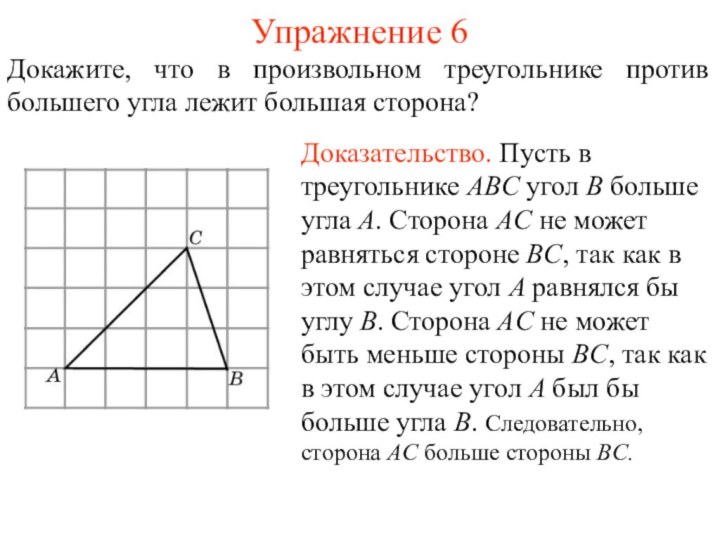
Упражнение 6
Докажите, что в произвольном треугольнике против большего
угла лежит большая сторона?
Доказательство. Пусть в треугольнике ABC угол
B больше угла A. Сторона AC не может равняться стороне BC, так как в этом случае угол A равнялся бы углу B. Сторона AC не может быть меньше стороны BC, так как в этом случае угол A был бы больше угла B. Следовательно, сторона AC больше стороны BC.
Слайд 9
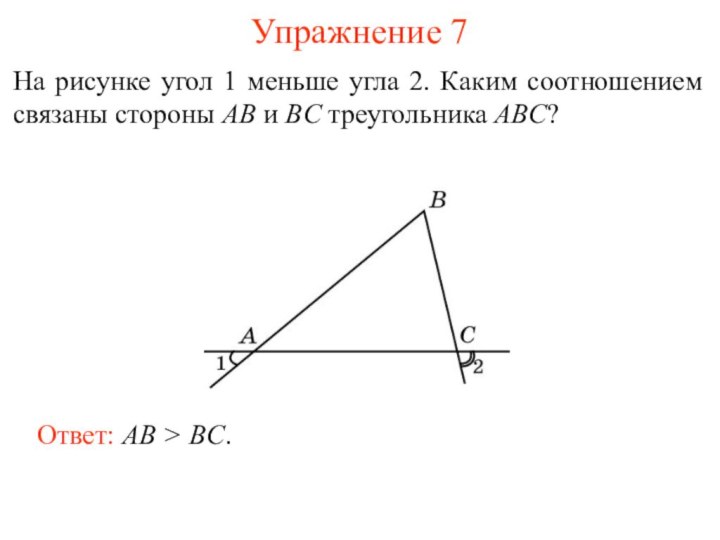
Упражнение 7
На рисунке угол 1 меньше угла 2.
Каким соотношением связаны стороны AB и BC треугольника ABC?
Ответ:
AB > BC.
Слайд 10
Упражнение 8
Ответ: а) BC > AC > AB;
Сравните
стороны треугольника ABC, если:
а) угол A больше угла
B, угол B больше угла C; б) угол A больше угла B, угол B равен углу C.
б) BC > AB, AC = AB.
Слайд 12
Упражнение 10
Какой вид имеет треугольник, если: а) два
его угла равны; б) три его угла равны?
Ответ:
а) Равнобедренный; б) правильный.
Слайд 17
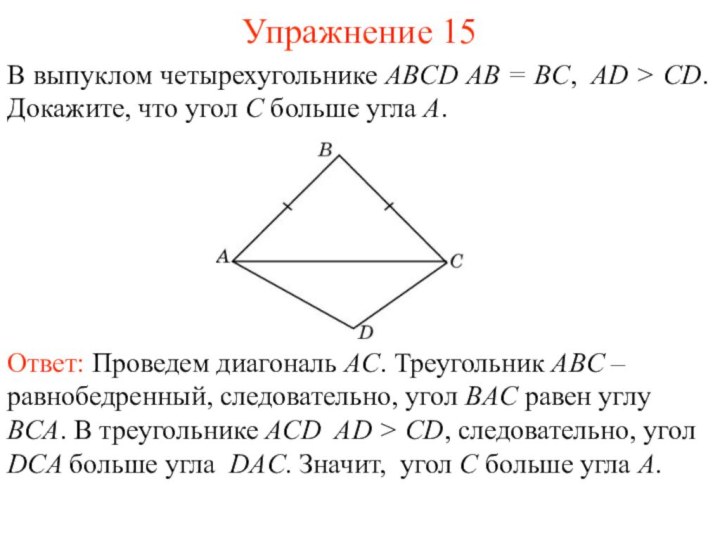
Упражнение 15
В выпуклом четырехугольнике ABCD AB = BC,
AD > CD. Докажите, что угол C больше угла
A.
Слайд 18
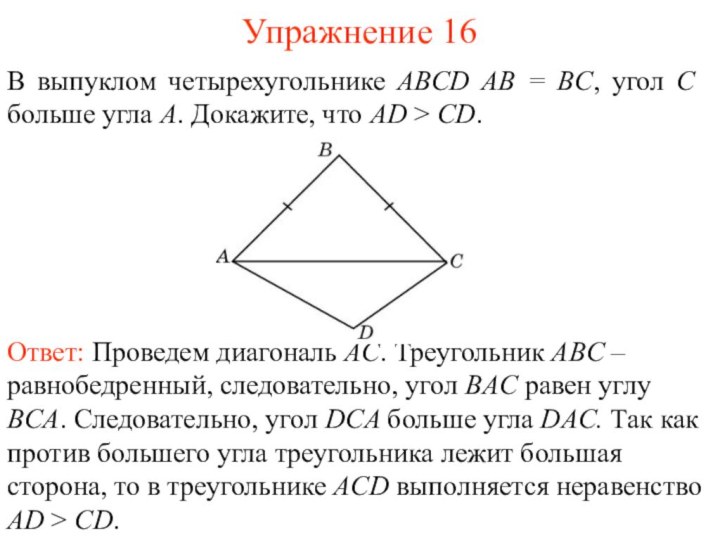
Упражнение 16
В выпуклом четырехугольнике ABCD AB = BC,
угол С больше угла A. Докажите, что AD >
CD.
Слайд 19
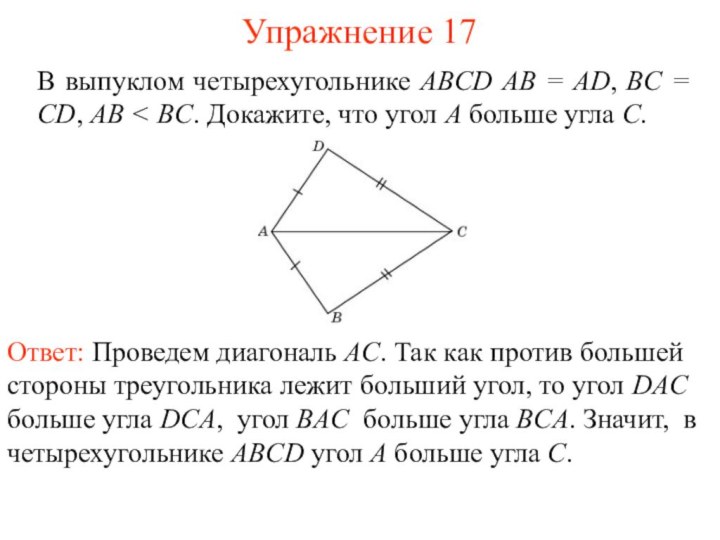
Упражнение 17
В выпуклом четырехугольнике ABCD AB = AD,
BC = CD, AB < BC. Докажите, что угол
A больше угла C.
Слайд 20
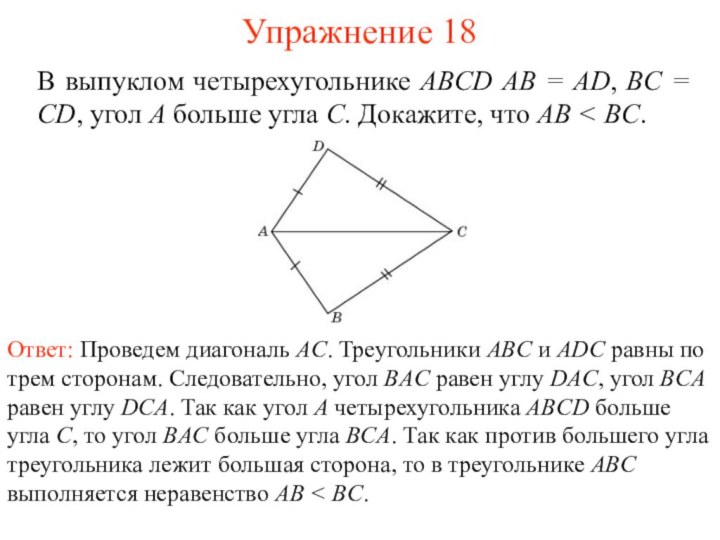
Упражнение 18
В выпуклом четырехугольнике ABCD AB = AD,
BC = CD, угол A больше угла C. Докажите,
что AB < BC.
Слайд 21
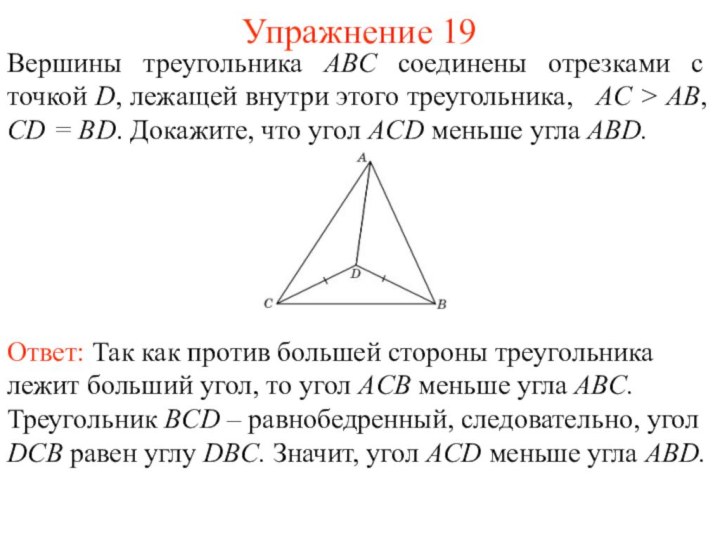
Упражнение 19
Вершины треугольника ABC соединены отрезками с точкой
D, лежащей внутри этого треугольника, AC > AB,
CD = BD. Докажите, что угол ACD меньше угла ABD.Ответ: Так как против большей стороны треугольника лежит больший угол, то угол ACB меньше угла ABC. Треугольник BCD – равнобедренный, следовательно, угол DCB равен углу DBC. Значит, угол ACD меньше угла ABD.
Слайд 22
Упражнение 20
Вершины треугольника ABC соединены отрезками с точкой
D, лежащей внутри этого треугольника, CD = BD, угол
ACD меньше угла ABD. Докажите, что AC > AB.Ответ: Треугольник BCD – равнобедренный, следовательно, угол DCB равен углу DBC. Значит, угол ACB меньше угла ABC. Так как против большего угла треугольника лежит большая сторона, то в треугольнике ABC выполняется неравенство AC > AB.
Слайд 23
Упражнение 21
Отрезки AE и BD пересекаются в точке
C, AB > BC, CD = DE. Докажите, что
угол BAC меньше угла DEC.Ответ: Так как AB > BC, то угол BAC меньше угла BCA. Так как CD = DE, то угол DEC равен углу DCE. Углы BCA и DCE равны как вертикальные. Значит, угол BAC меньше угла DEC.
Слайд 24
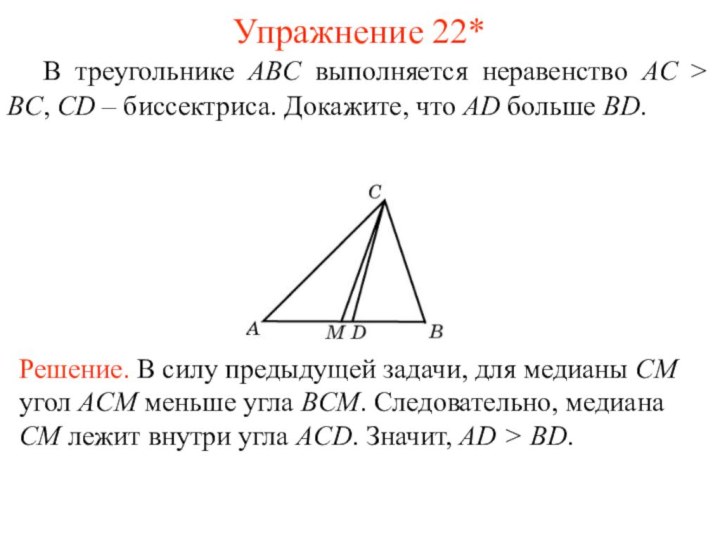
Упражнение 22
Отрезки AE и BD пересекаются в точке
C, CD = DE, угол BAC меньше угла DEC.
Докажите, что AB > BC.Ответ: Так как CD = DE, то угол DEC равен углу DCE. Углы BCA и DCE равны как вертикальные. Так как угол BAC меньше угла DEC, то угол BAC меньше угла BCA. Значит, угол AB > BC.