Презентация на тему по теме: Шестиугольная пирамида (11 класс)

Содержание

2. Правильная шестиугольная пирамида Правильная шестиугольная пирамида — пирамида, в основании которой лежит правильный шестиугольник.
3. Свойства пирамиды Если все боковые рёбра
5. Площадь основания пирамиды В основаниях
6. Объём пирамиды Объем пирамиды вычисляется
7. Высота пирамиды Прямая SO является высотой пирамиды,
8. Правильный шестиугольник в основании пирамиды
9. Скачать презентацию
10. Похожие презентации

Правильная шестиугольная пирамида Правильная шестиугольная пирамида — пирамида, в основании которой лежит правильный шестиугольник.

Главная
Геометрия
Презентация по теме: Шестиугольная пирамида (11 класс)

Правильная шестиугольная пирамида Правильная шестиугольная пирамида — пирамида, в основании которой лежит правильный шестиугольник.

Свойства пирамиды Если все боковые рёбра равны, то: Вокруг

Презентация по теме: Шестиугольная пирамида (11 класс)

Площадь основания пирамиды В основаниях пирамиды находится правильный шестиугольник со

Объём пирамиды Объем пирамиды вычисляется как треть произведения площади ее

Высота пирамиды Прямая SO является высотой пирамиды, поэтому ∠SOF=90∘. Треугольник SOF прямоугольный, в нем FO=a, FS=h. По

Правильный шестиугольник в основании пирамиды По свойствам правильного шестиугольника, треугольники

Находим ST и TO Пусть точка T является серединой ребра AF. Треугольник AOF правильный, поэтому, по cвойствам правильного

Слайды презентации

Слайд 2 Правильная шестиугольная пирамида
Правильная шестиугольная пирамида — пирамида,

в основании которой лежит правильный шестиугольник.

Слайд 3 Свойства пирамиды
Если все боковые рёбра равны,

Свойства пирамиды Если все боковые рёбра равны, то: Вокруг основания

то:
Вокруг основания пирамиды можно описать окружность,

причём вершина пирамиды проецируется в её центр;
Боковые рёбра образуют с плоскостью основания равные углы;
Также верно и обратное, то есть если боковые рёбра образуют с плоскостью основания равные углы, или если около основания пирамиды можно описать окружность, причём вершина пирамиды проецируется в её центр, то все боковые рёбра пирамиды равны.
Если боковые грани наклонены к плоскости основания под одним углом, то:
В основание пирамиды можно вписать окружность, причём вершина пирамиды проецируется в её центр;
Высоты боковых граней равны;
Площадь боковой поверхности равна половине произведения периметра основания на высоту боковой грани.

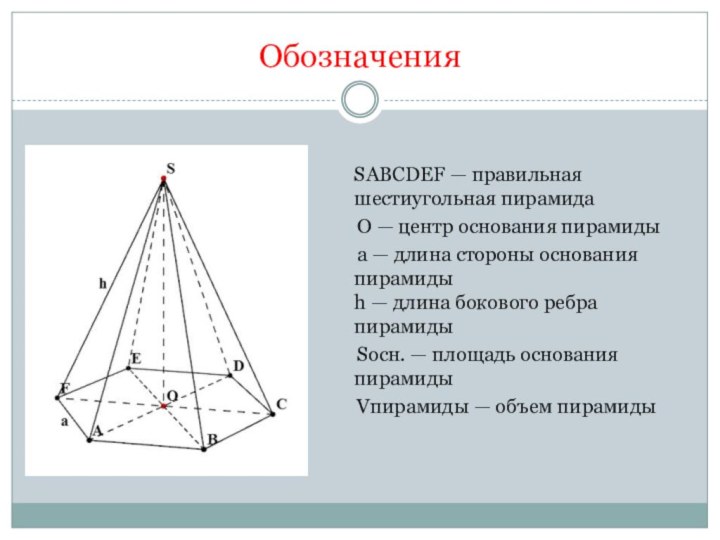
Слайд 4 Обозначения
SABCDEF — правильная шестиугольная пирамида

O — центр основания пирамиды
a — длина

стороны основания пирамиды h — длина бокового ребра пирамиды
Sосн. — площадь основания пирамиды
Vпирамиды — объем пирамиды

Слайд 5 Площадь основания пирамиды
В основаниях пирамиды находится правильный

шестиугольник со стороной a. По свойствам правильного шестиугольника, площадь основания пирамиды равна

Sосн.=

Слайд 6 Объём пирамиды
Объем пирамиды вычисляется как

треть произведения площади ее основания на ее высоту. Высотой

правильной пирамиды является отрезок SO. В основании правильной шестиугольной призмы находится правильный шестиугольник, площадь которого нам известна. Получаем V пирамиды=
Sосн.⋅SO

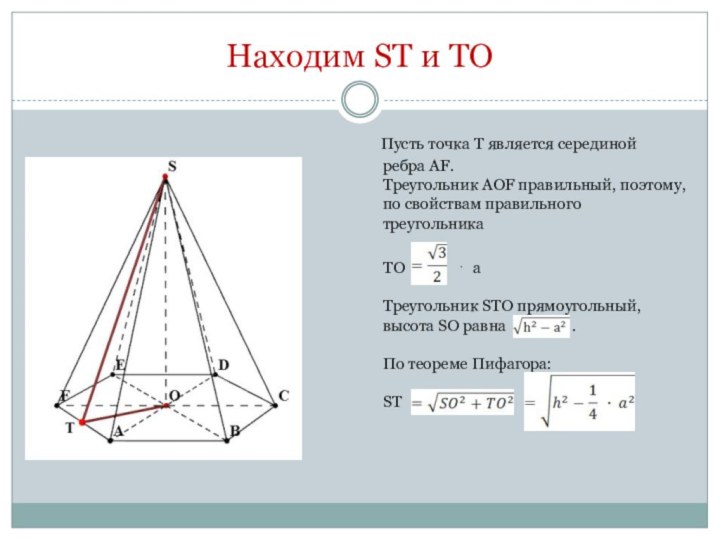
Слайд 7 Высота пирамиды
Прямая SO является высотой пирамиды, поэтому ∠SOF=90∘.

Треугольник SOF прямоугольный, в нем FO=a, FS=h. По свойствам прямоугольного треугольника SO

Слайд 8 Правильный шестиугольник в основании пирамиды
По

свойствам правильного шестиугольника, треугольники AOB, BOC, COD, DOE, EOF,

FOA являются правильными треугольниками. Отсюда следует, что AO=OD=EO=OB=CO=OF=a Проводим отрезок AE, пересекающийся с отрезком CF в точке M. Треугольник AEO равнобедренный, в нём AO=OE=a, ∠EOA=120∘. По свойствам равнобедренного треугольника AE= a ⋅ a Аналогичным образом приходим к заключению, что AC=CE a
FM=MO= a

⋅