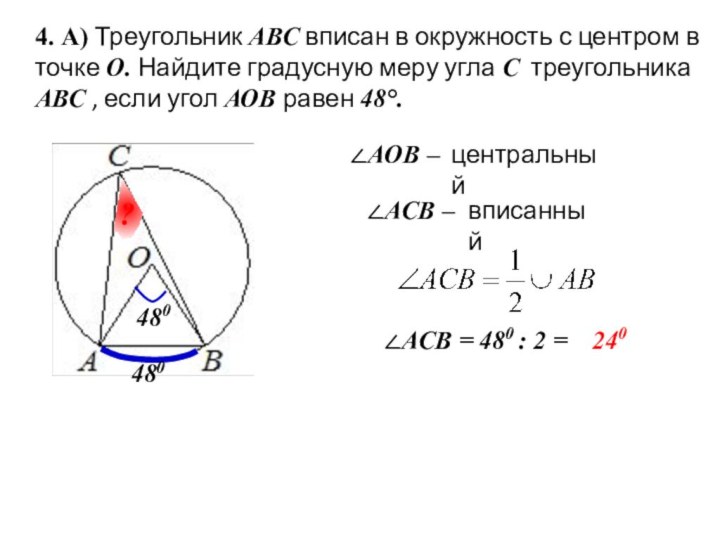
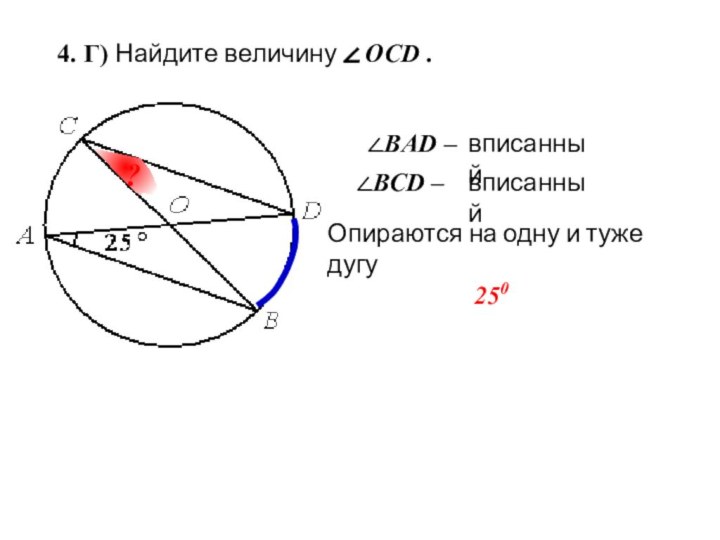
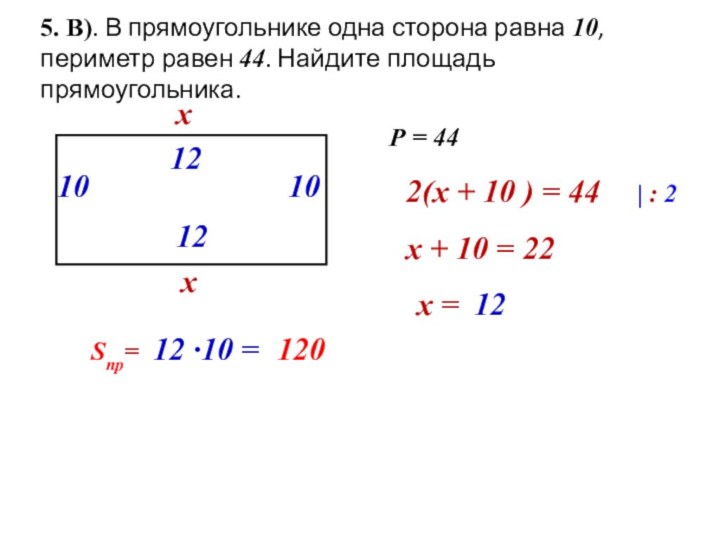
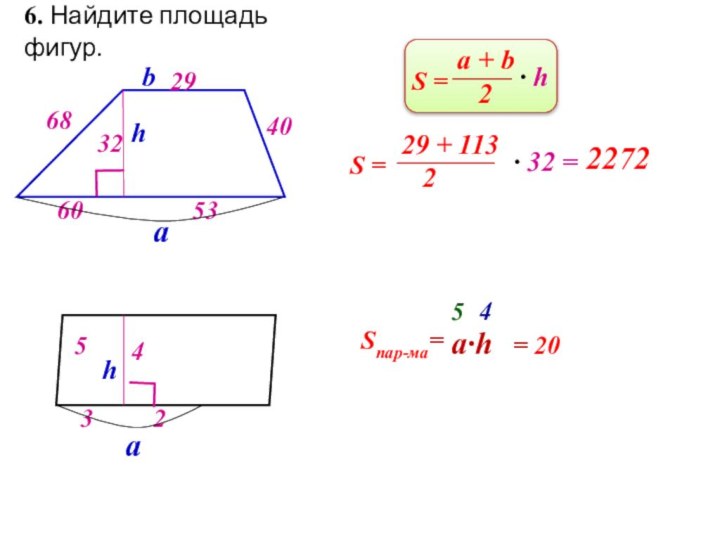
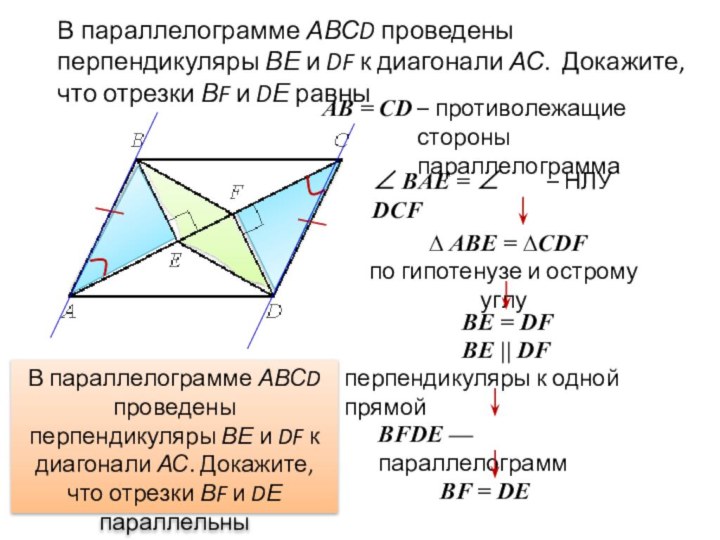
вертикальном положении, находится на высоте 3,2 м от земли.
Длина троса равна 4 метра. Найдите расстояние от основания флагштока до места крепления троса на земле.4 м
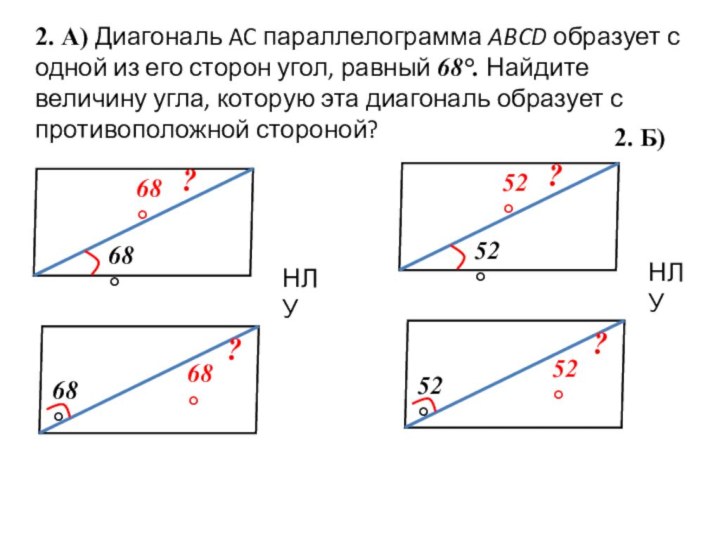
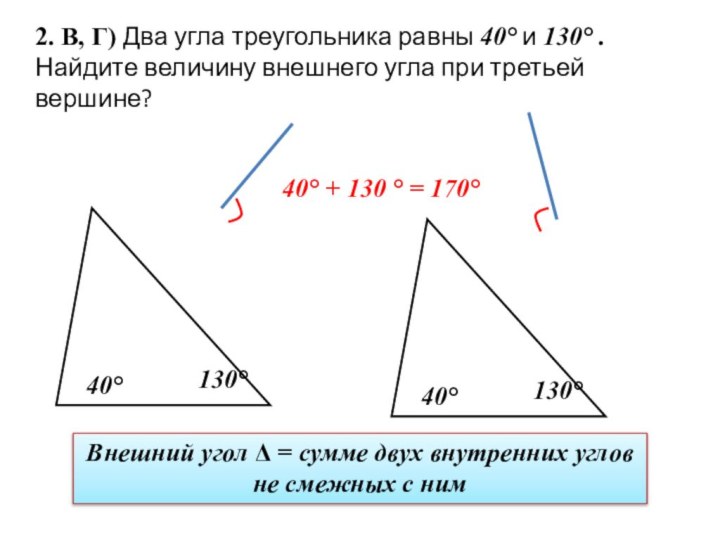
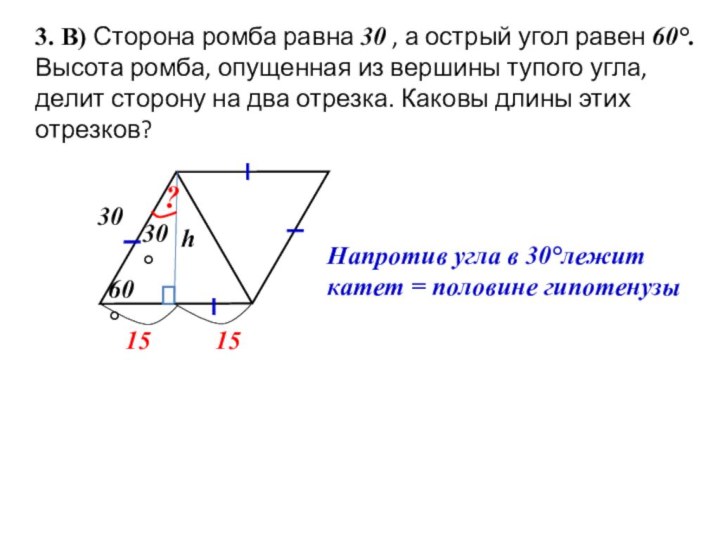
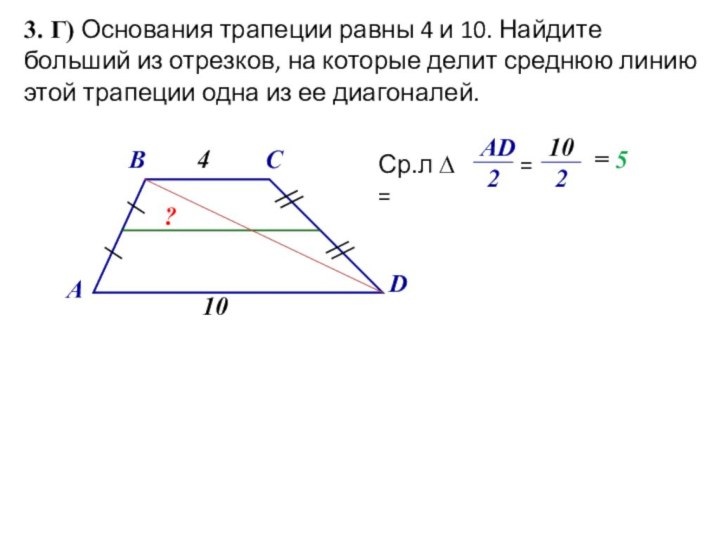
3,2 м
?
с
а
b
По т.Пифагора:
с2 = а2 + b2
42 = 3,22 + b2
16= 10,24 + b2
16 – 10,24 = b2
b2 =
5,76
b =
b =
2,4
Ответ: 2,4