15
ИГРАТЬ 21
СПАТЬ 5
СМЕЯТЬСЯ 2
ЕСТЬ, ЖЕВАТЬ 5
СПИСЫВАТЬ 7
Чего нельзя делать на уроке,
но очень хочется?
1
2
3
4
5
6
Слайд 3
Психологическая установка
На уроке можно:
ошибаться,
сомневаться,
консультироваться.
Слайд 4
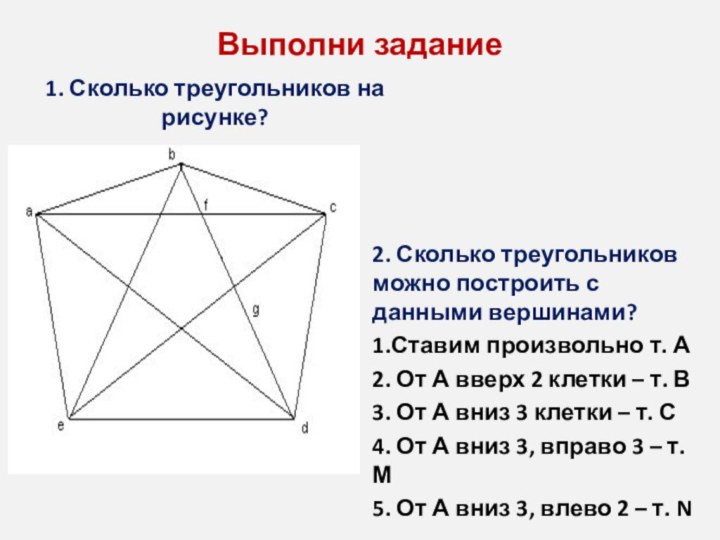
Выполни задание
1. Сколько треугольников на рисунке?
2. Сколько треугольников
можно построить с данными вершинами?
1.Ставим произвольно т. А
2. От
А вверх 2 клетки – т. В
3. От А вниз 3 клетки – т. С
4. От А вниз 3, вправо 3 – т. М
5. От А вниз 3, влево 2 – т. N
Слайд 5
Тема урока «Треугольники»
Урок П+П (повторение +
познание)
Цель: повторить всё о треугольниках.
Аукцион « Т
р е у г о л ь н и к и »
Слайд 6
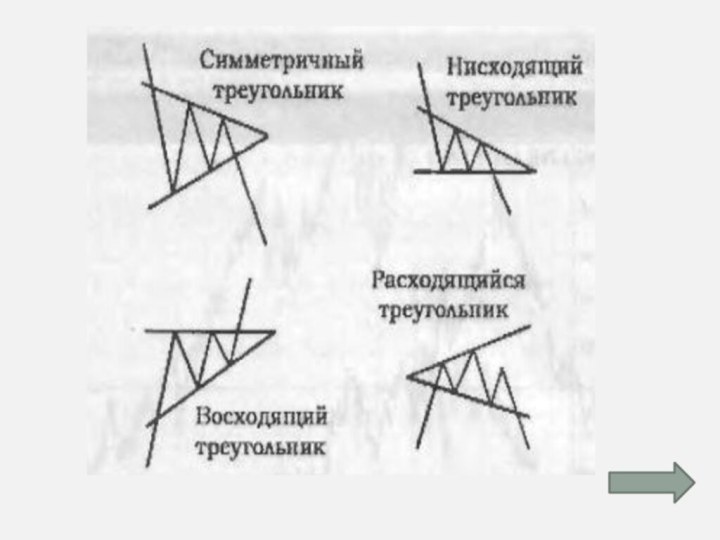
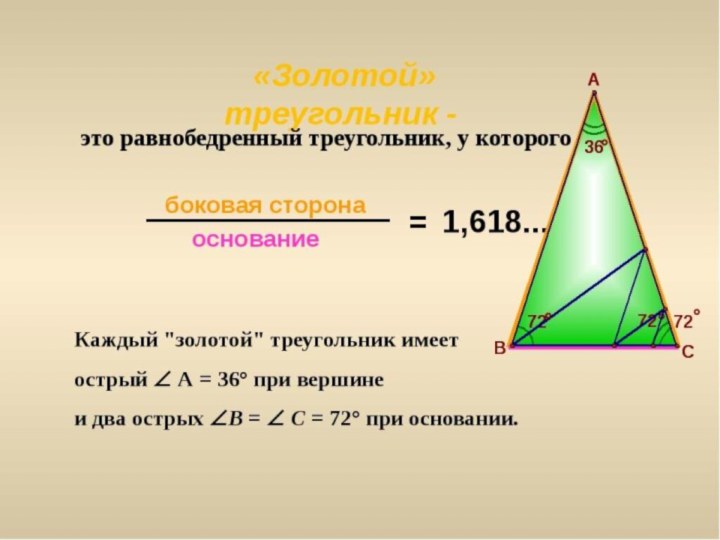
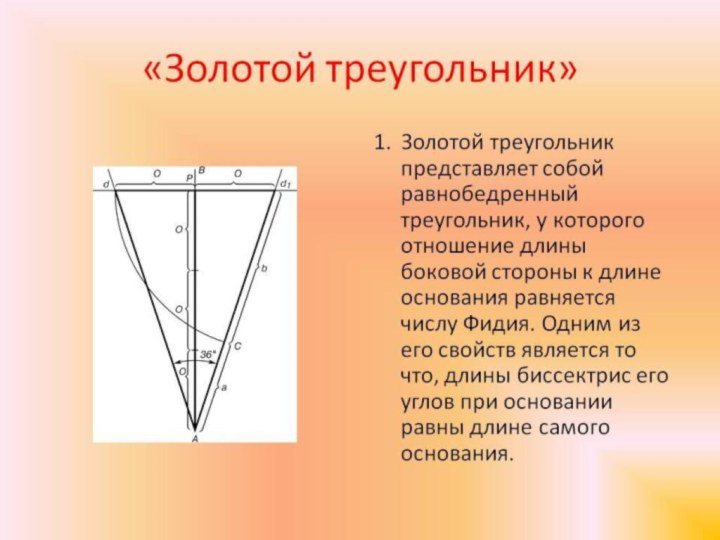
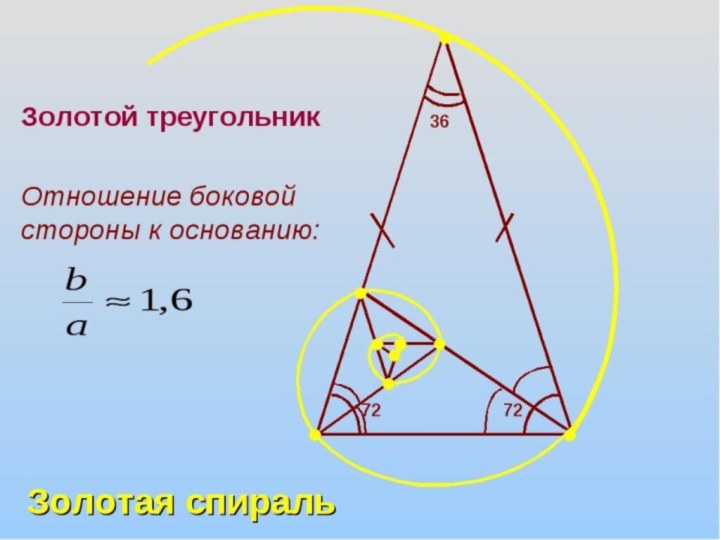
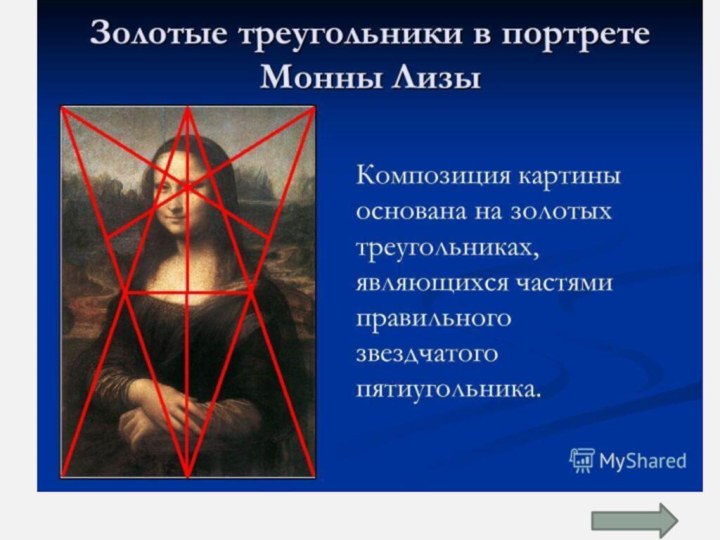
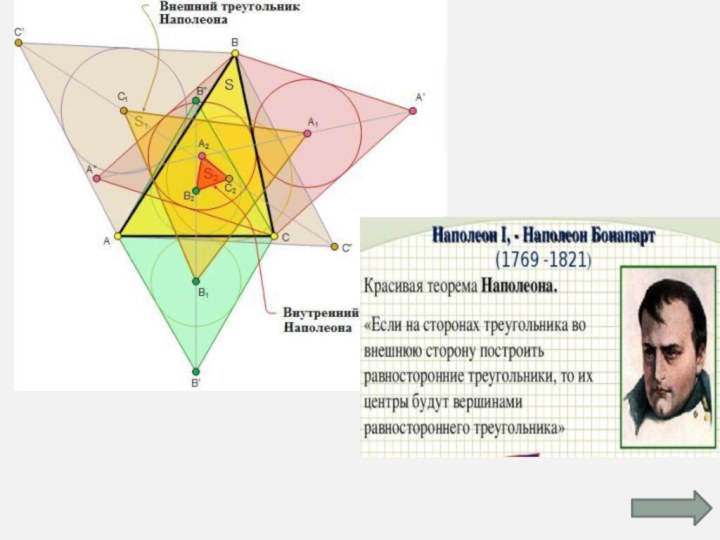
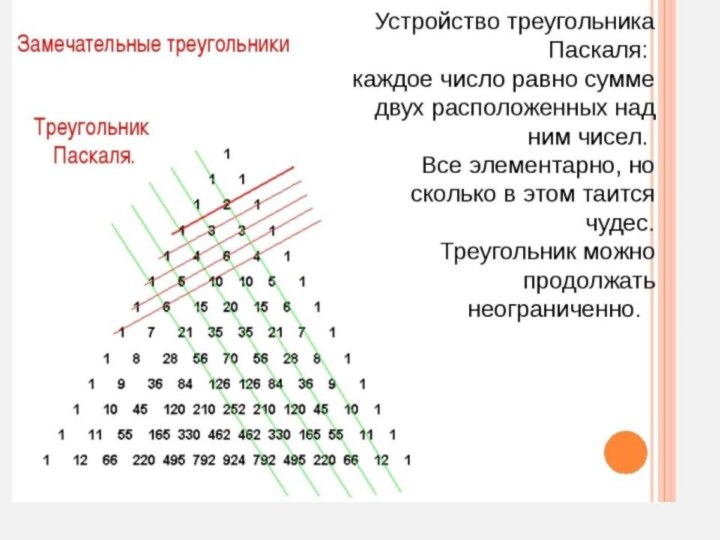
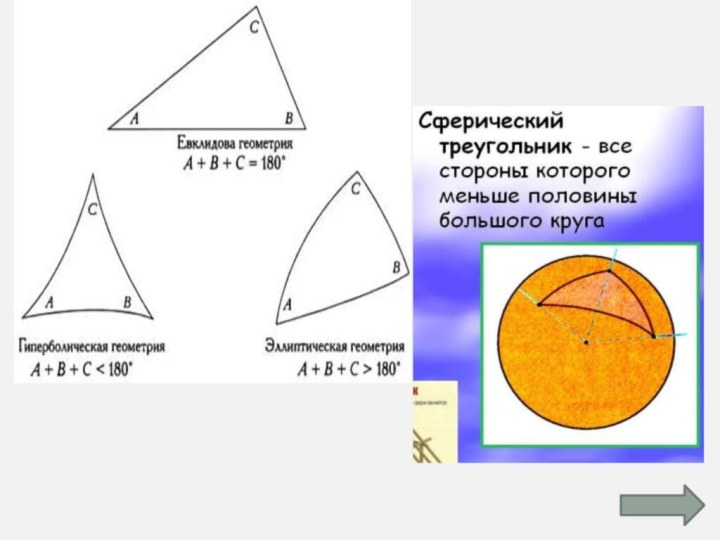
Какие треугольники
вы ещё знаете,
о каких треугольниках
слышали?
Слайд 24
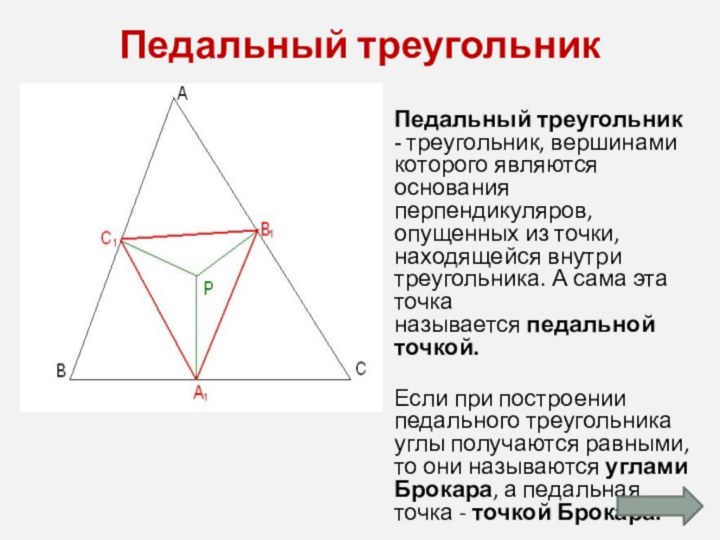
Педальный треугольник
Педальный треугольник - треугольник, вершинами которого являются основания
перпендикуляров, опущенных из точки, находящейся внутри треугольника. А сама
эта точка называется педальной точкой.
Если при построении педального треугольника углы получаются равными, то они называются углами Брокара, а педальная точка - точкой Брокара.
Слайд 26
Сегодня я узнал…
Было интересно…
Было трудно…
Я выполнял задания…
Меня удивило…
Теперь
я могу…
Подведем итоги
Слайд 27
Домашнее задание.
Творческая работа.
Провести
исследовательскую работу
по теме «Педальный треугольник»
Слайд 28
«Ученик, который учится без желания –
это
птица без крыльев» .
древнегреческий философ Саади
И мне
хотелось бы, чтобы было у вас желание учиться, узнавать новое, неопознанное не только сегодня, а всегда. И только в этом случае своими «крыльями» вы будете взлетать все выше и выше.
Высоких полётов вам!
Слайд 31
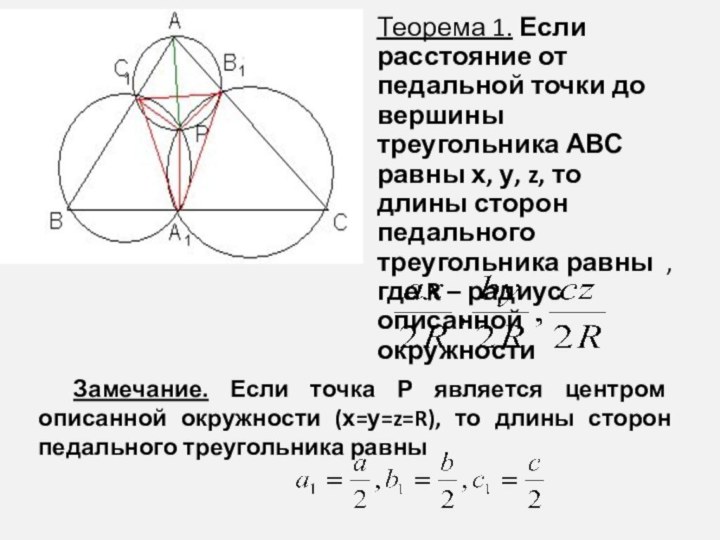
Теорема 1. Если расстояние от педальной точки до
вершины треугольника АВС равны х, у, z, то длины
сторон педального треугольника равны , где R – радиус описанной окружности
Замечание. Если точка Р является центром описанной окружности (х=у=z=R), то длины сторон педального треугольника равны
.
Слайд 32
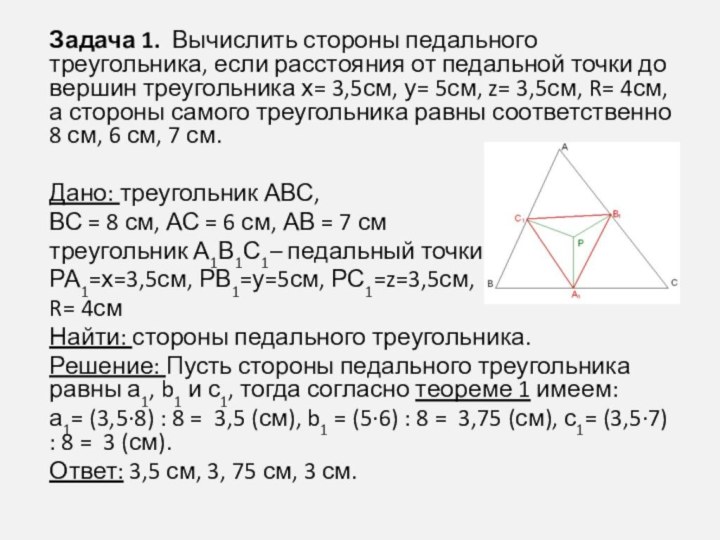
Задача 1. Вычислить стороны педального треугольника, если расстояния
от педальной точки до вершин треугольника х= 3,5см, у=
5см, z= 3,5см, R= 4см, а стороны самого треугольника равны соответственно 8 см, 6 см, 7 см.
Дано: треугольник АВС,
ВС = 8 см, АС = 6 см, АВ = 7 см
треугольник А1В1С1– педальный точки Р,
РА1=х=3,5см, РВ1=у=5см, РС1=z=3,5см,
R= 4см
Найти: стороны педального треугольника.
Решение: Пусть стороны педального треугольника равны а1, b1 и с1, тогда согласно теореме 1 имеем:
а1= (3,5∙8) : 8 = 3,5 (см), b1 = (5∙6) : 8 = 3,75 (см), с1= (3,5∙7) : 8 = 3 (см).
Ответ: 3,5 см, 3, 75 см, 3 см.
Слайд 33
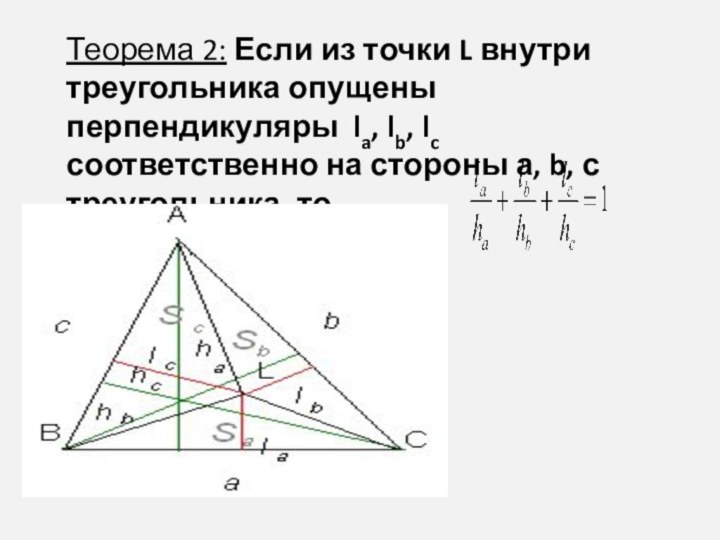
Теорема 2: Если из точки L внутри треугольника
опущены перпендикуляры la, lb, lc соответственно на стороны а,
b, с треугольника, то