Что такое findslide.org?

FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.

Обратная связь

Презентация на тему Многограники 11 кл

Содержание

2. Многогранник – это поверхность, составленная из многоугольников
5. У всех многогранников есть общие свойстваВсе они
6. Каждое ребро многоугольника соединяет две, и только
7. Выпуклость означает, что тело полностью расположено только
8. Многогранники можно условно разделить на:
9. Невыпуклым многогранником называется такой многогранник, у которого
10. Выпуклый многогранник характеризуется тем, что он расположен по одну сторону от плоскости каждой своей грани.
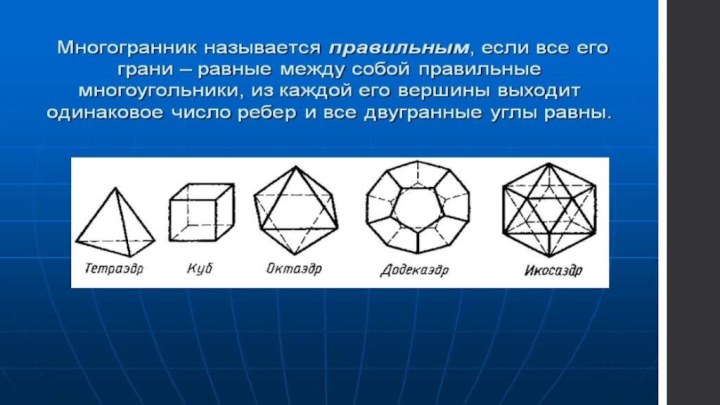
12. Выпуклые делятся на:Правильные(Платоновые тела)Полуправильные(Архимедовы тела)Обычные(призма, пирамида, параллелепипед)
13. Обычные многогранники
16. Конгруэнтность – это согласованность разных элементов, объектов,
21. Построение сечений многогранников.Правила построения сечений многогранников:1) проводим
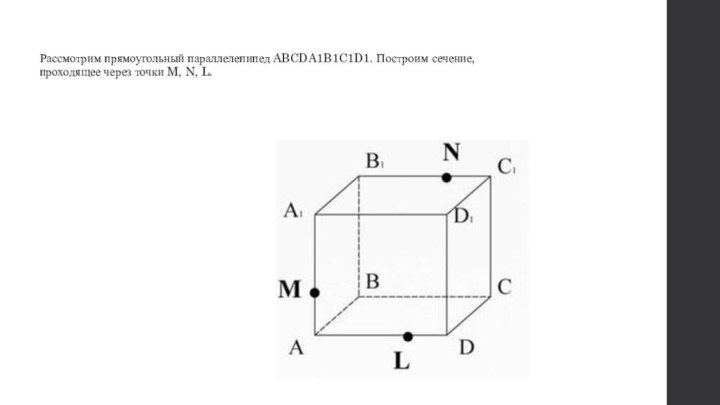
22. Рассмотрим прямоугольный параллелепипед ABCDA1B1C1D1. Построим сечение, проходящее через точки M, N, L.
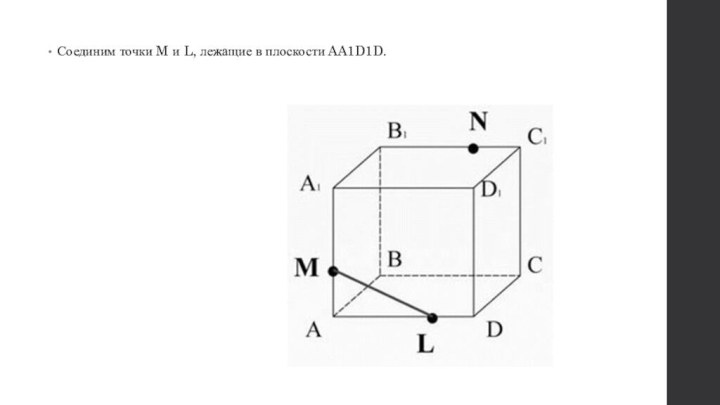
23. Соединим точки M и L, лежащие в плоскости AA1D1D.
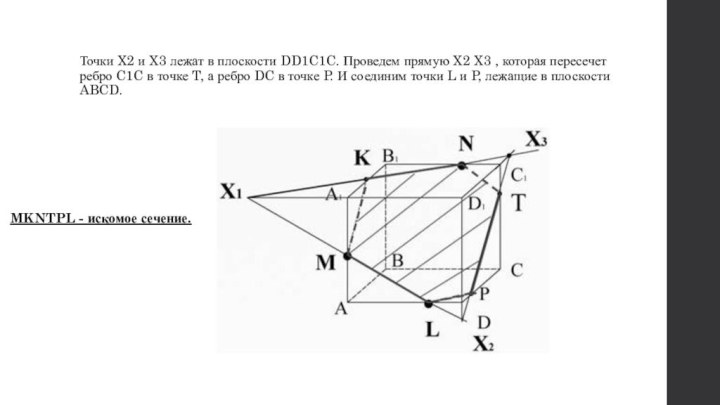
24. Пересечем прямую ML ( принадлежащую сечению) с
25. Точка X1 лежит на ребре A1D1, а
26. Соединим точки K и M, лежащие в одной плоскости AA1B1B.
27. Найдем прямую пересечения плоскости сечения с плоскостью
28. пересечем прямую KN (принадлежащую сечению) с ребром
29. Скачать презентацию
30. Похожие презентации

Многогранник – это поверхность, составленная из многоугольников и ограничивающая некоторое геометрическое тело. Это тело также называется многогранником.

У всех многогранников есть общие свойстваВсе они имеют 3 неотъемлемых компонента: грань

Каждое ребро многоугольника соединяет две, и только две грани, которые по отношению

Выпуклость означает, что тело полностью расположено только по одну сторону плоскости, на

Многогранники можно условно разделить на:

Невыпуклым многогранником называется такой многогранник, у которого найдется по крайней мере одна

Выпуклый многогранник характеризуется тем, что он расположен по одну сторону от плоскости каждой своей грани.

Выпуклые делятся на:Правильные(Платоновые тела)Полуправильные(Архимедовы тела)Обычные(призма, пирамида, параллелепипед)

Конгруэнтность – это согласованность разных элементов, объектов, компонентов какой-нибудь структуры, их слаженная

Построение сечений многогранников.Правила построения сечений многогранников:1) проводим прямые через точки, лежащие в

Рассмотрим прямоугольный параллелепипед ABCDA1B1C1D1. Построим сечение, проходящее через точки M, N, L.

Соединим точки M и L, лежащие в плоскости AA1D1D.

Пересечем прямую ML ( принадлежащую сечению) с ребром A1D1, они лежат в

Точка X1 лежит на ребре A1D1, а значит и плоскости A1B1C1D1, соединим

Соединим точки K и M, лежащие в одной плоскости AA1B1B.

Найдем прямую пересечения плоскости сечения с плоскостью DD1C1C: пересечем прямую ML

пересечем прямую KN (принадлежащую сечению) с ребром D1C1, они лежат в одной

Точки X2 и X3 лежат в плоскости DD1C1C. Проведем прямую X2 X3

Слайды презентации

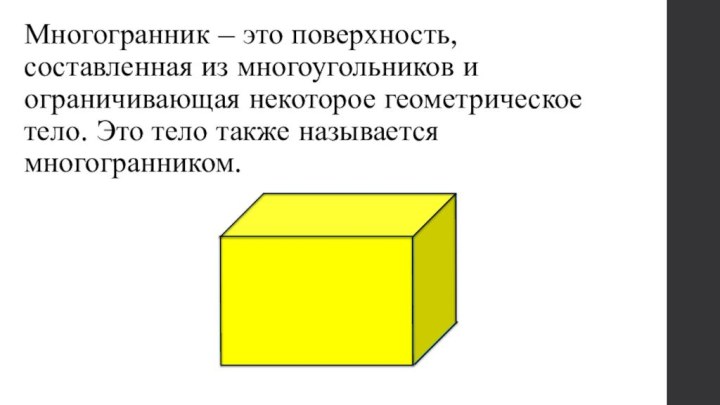
Слайд 2 Многогранник – это поверхность, составленная из многоугольников и

Многогранник – это поверхность, составленная из многоугольников и ограничивающая некоторое геометрическое

ограничивающая некоторое геометрическое тело. Это тело также называется многогранником.

Слайд 5 У всех многогранников есть общие свойства
Все они имеют

У всех многогранников есть общие свойстваВсе они имеют 3 неотъемлемых компонента:

3 неотъемлемых компонента: грань (поверхность многоугольника), вершина (углы, образовавшиеся

в местах соединения граней), ребро (сторона фигуры или отрезок, образованный в месте стыка двух граней).

Грань

Ребро

Вершина

А1

В1

С1

Д1

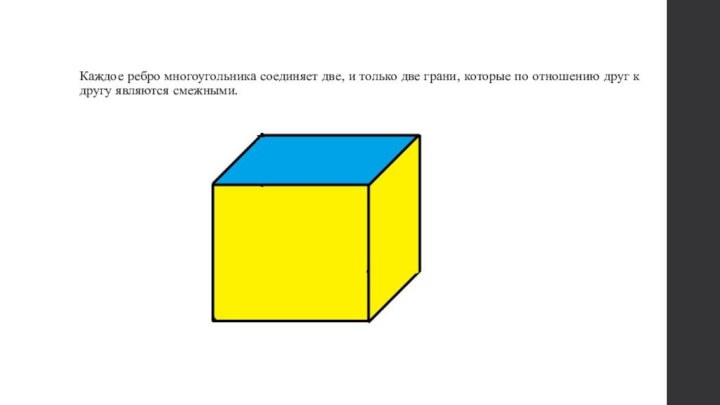
Слайд 6 Каждое ребро многоугольника соединяет две, и только две

Каждое ребро многоугольника соединяет две, и только две грани, которые по

грани, которые по отношению друг к другу являются смежными.

Слайд 7 Выпуклость означает, что тело полностью расположено только по

Выпуклость означает, что тело полностью расположено только по одну сторону плоскости,

одну сторону плоскости, на которой лежит одна из граней.

Правило применимо ко всем граням многогранника. Такие геометрические фигуры в стереометрии называют термином выпуклые многогранники. Исключение составляют звёздчатые многогранники, которые являются производными правильных многогранных геометрических тел.

Слайд 8 Многогранники можно условно разделить на:

Слайд 9 Невыпуклым многогранником называется такой многогранник, у которого найдется

Невыпуклым многогранником называется такой многогранник, у которого найдется по крайней мере

по крайней мере одна грань такая, что плоскость, проведенная

через эту грань, делит данный многогранник на две или более частей.

Слайд 10 Выпуклый многогранник характеризуется тем, что он расположен по

одну сторону от плоскости каждой своей грани.

Слайд 11

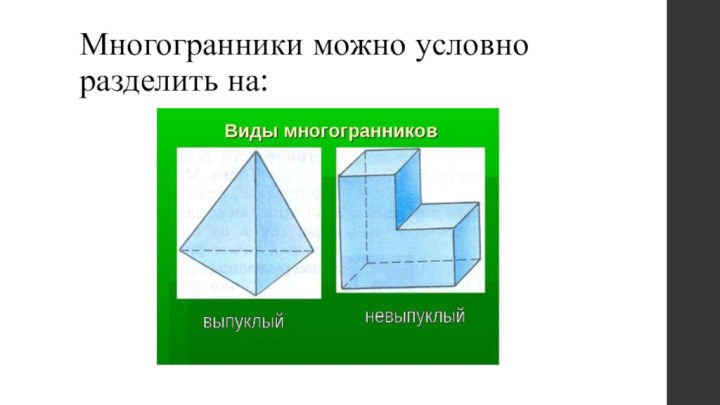
Слайд 12 Выпуклые делятся на:
Правильные
(Платоновые тела)
Полуправильные
(Архимедовы тела)
Обычные
(призма, пирамида, параллелепипед)

Слайд 13 Обычные многогранники

Слайд 14

Слайд 15

Слайд 16 Конгруэнтность – это согласованность разных элементов, объектов, компонентов

Конгруэнтность – это согласованность разных элементов, объектов, компонентов какой-нибудь структуры, их

какой-нибудь структуры, их слаженная работа и соответствие друг другу,

благодаря которому достигается гармоничная работа и целостность общей структуры

Слайд 17

Слайд 18

Слайд 19

Слайд 20

Слайд 21 Построение сечений многогранников.

Правила построения сечений многогранников:

1) проводим прямые

Построение сечений многогранников.Правила построения сечений многогранников:1) проводим прямые через точки, лежащие

через точки, лежащие в одной плоскости;

2) ищем прямые пересечения

плоскости сечения с гранями многогранника, для этого

а) ищем точки пересечения прямой принадлежащей плоскости сечения с прямой, принадлежащей одной из граней (лежащие в одной плоскости);

б) параллельные грани плоскость сечения пересекает по параллельным прямым.