Что такое findslide.org?

FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.

Для правообладателей

Обратная связь

Email: Нажмите что бы посмотреть 

Яндекс.Метрика

Презентация на тему Тема Площади 8 класс

Содержание

Цели урока: Обобщить теоретический материал по теме «Площади» Совершенствовать навыки решения задач на применение формул вычисления площадей
ГЕОМЕТРИЯ 8 КЛАСС«Площади треугольника, параллелограмма и трапеции »(Урок обобщения, систематизациии контроля знаний и умений) Цели урока: Обобщить теоретический материал по теме «Площади» домашнее задание (выбери уровень работы А,Б,В). План урока:разминка (проверка теоретических знаний);проверка домашнего Правила работы на урокеПо ходу урока заполняются оценочные листы;В конце урока подсчитываются Разминка! Площади:S= a hS= ½ d1d2 S=1/2(a+b)hS=a2S=abS=1/2d2S=1/2 ah СЛЕДСТВИЯ1. S=1/2ab2. S1:S2= a1:a2, если h1=h23. 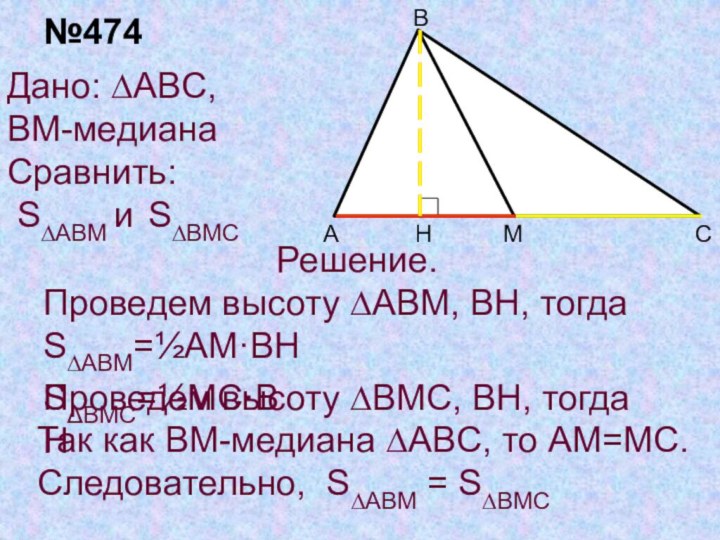S1:S2=(a1b1):(a2b2), если a1۸ b1= Проверка домашнего задания№481, №474 HДано: ∆ABC, BM-медиана Сравнить: S∆ABM и S∆BMCРешение. Проведем высоту ∆ABM, BH, тогда №481Дано:ABCD –трапеция, ADAB, AB=BC=6см, BCD=135° Найти: SABCDРешениеSABCD=½(AD+BC)·ABТак как ADAB, тоHПроведем CHAD и Теоретический тестс последующей взаимопроверкой ПРОВЕРЬ СЕБЯ !             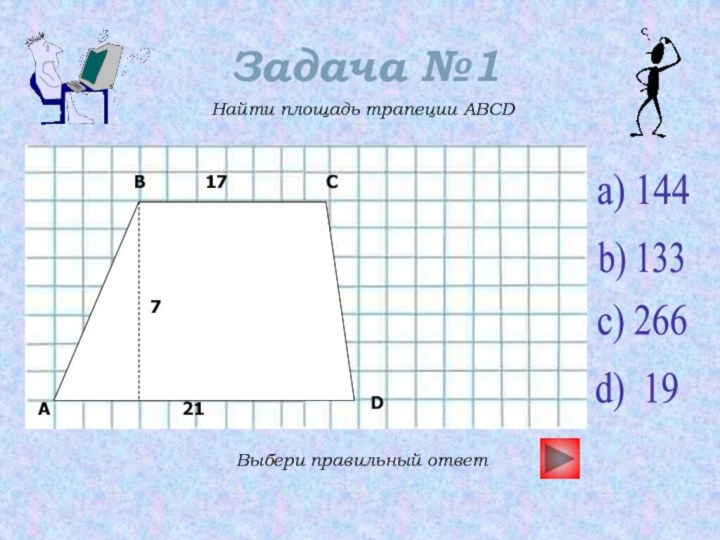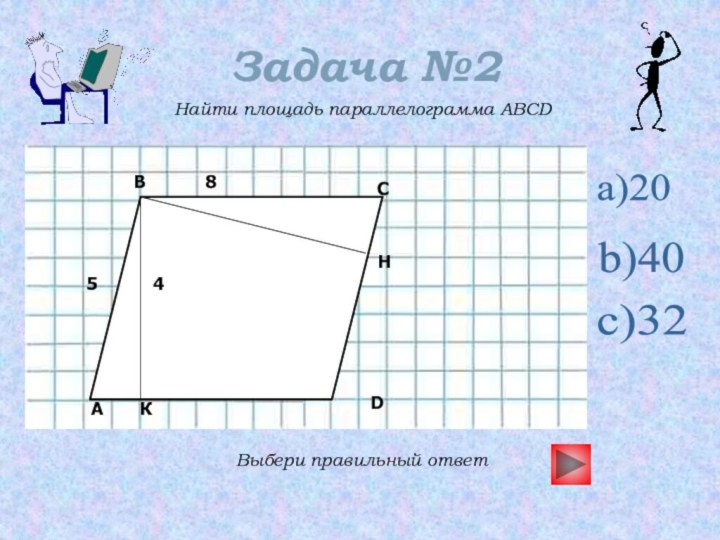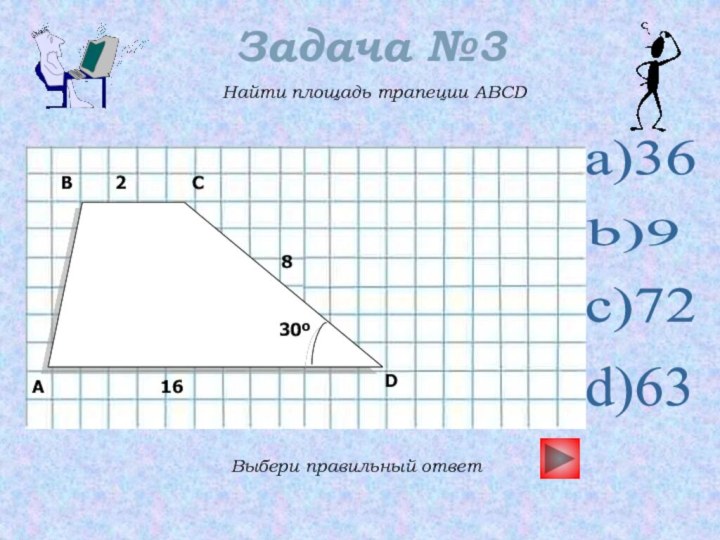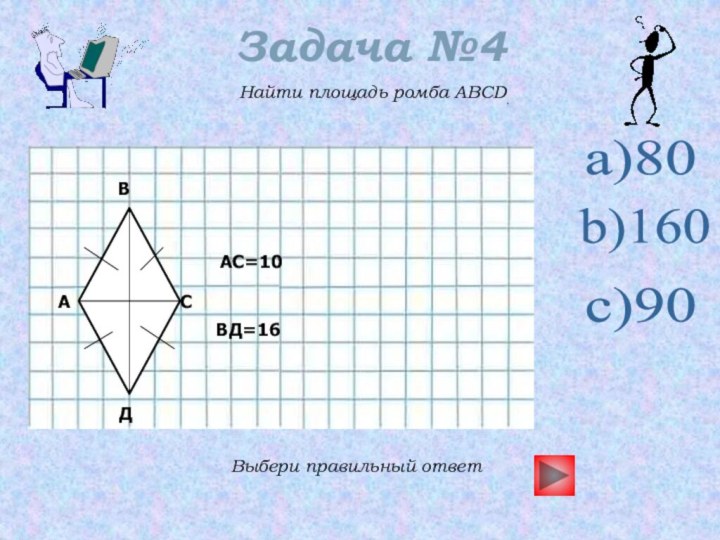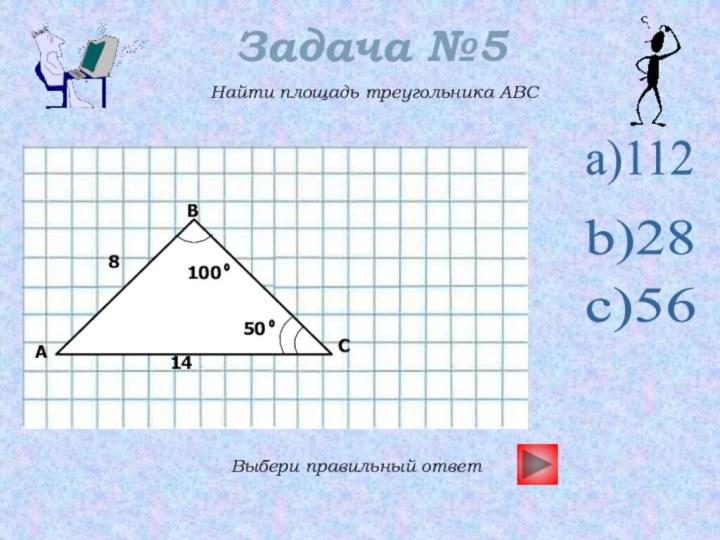бававаббв1 задание2 задание3 задание6 задание4 задание1 задание2 задание3 Задача №1Найти площадь трапеции ABCDВыбери правильный ответa) 144b) 133c) 266d) 19 Задача №2Найти площадь параллелограмма ABCDВыбери правильный ответa)20b)40c)3245H Задача №3Найти площадь трапеции ABCDВыбери правильный ответa)36b)9c)72d)63 Задача №4Найти площадь ромба ABCD.Выбери правильный ответa)80b)160c)90Д Задача №5Найти площадь треугольника ABCВыбери правильный ответa)112c)5614810050b)28 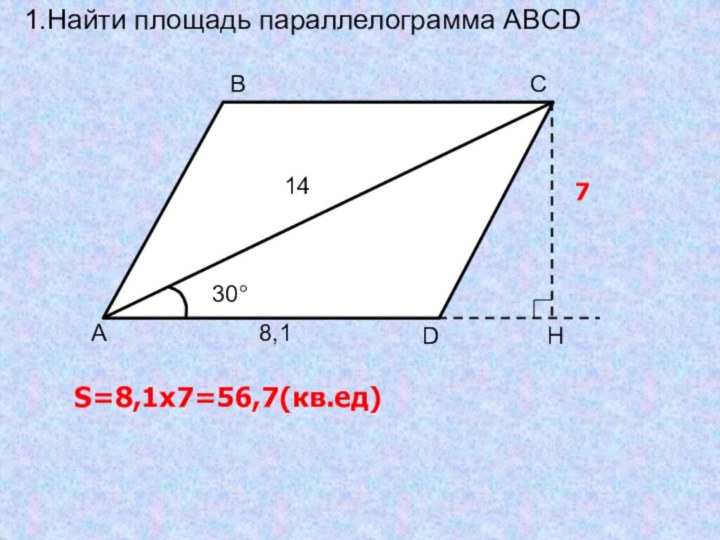1.Найти площадь параллелограмма ABCDHS=8,1x7=56,7(кв.ед)7 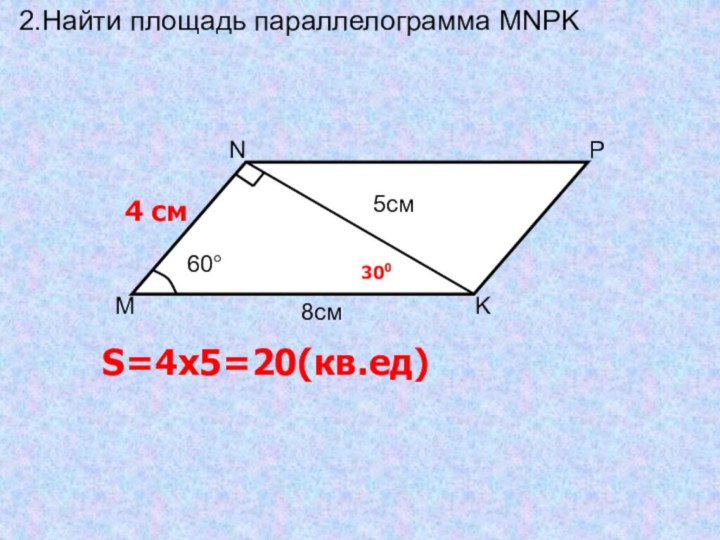2.Найти площадь параллелограмма MNPK4 смS=4x5=20(кв.ед)300 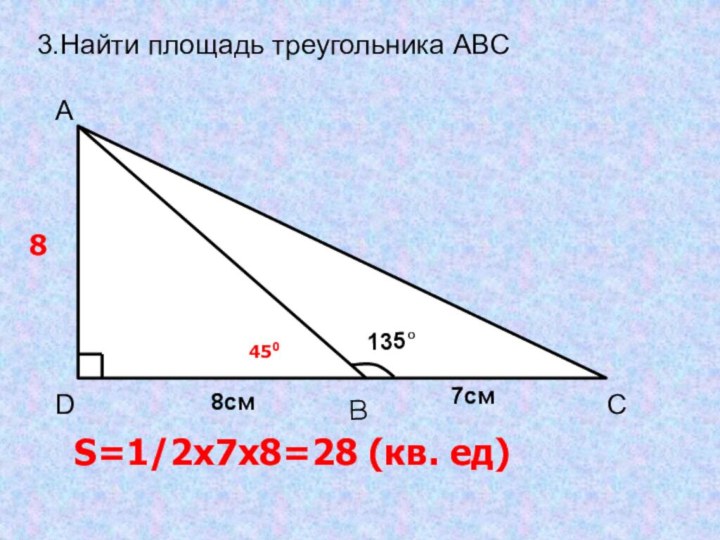3.Найти площадь треугольника ABC8450S=1/2x7x8=28 (кв. 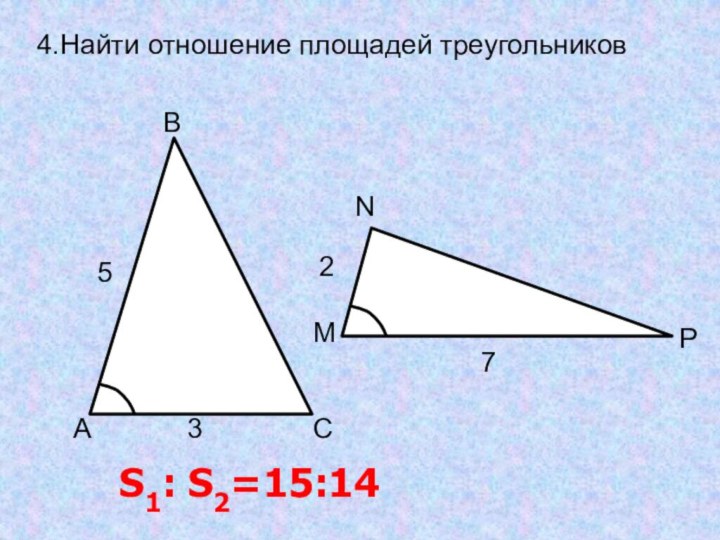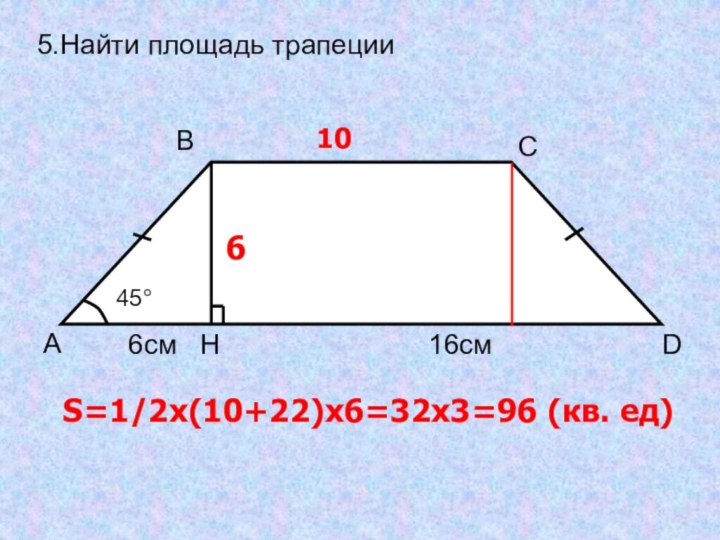ед) 4.Найти отношение площадей треугольников S1: S2=15:14 5.Найти площадь трапеции106S=1/2x(10+22)x6=32x3=96 (кв. ед) Самостоятельная работа. 1, 2 вариант Проверь себя! Вариант 11.5см10смS=½·a·h; h=2·5=10(см)S=½·5·10=25(см2)Вариант 21.6см18смS=½·a·h; h=18:3=69(cм)S=½·18·6=54(см2) Вариант 1Вариант 22.2.30º8см6смS = a·h; h = ½·6=3(см); S = 8·3=24(см2)30º150ºS = Вариант 1Вариант 23.3.11cм7cм45ºS=½·(a+b)·h;h=4см; S=½·(11+7)·4; S=36см245º20cм6cм8cмS=½·(a+b)·h; h=6см; b=2O-2·6=8(см); S=½·(2O+8)·6=84см2 Вариант 1№4.HЕсли высоты двух треугольников равны, то их площади относятся как основания.ABC MBC и MCK имеют общую высоту MN, а основание BC в два Вариант 2№4.HKЕсли высоты двух треугольников равны, то их площади относятся как основания.ABK Проверь себя!1. Сумма длин всех сторон5.Отрезок, соединяющий противолежащие вершины6. Прямоугольник, итог урока Домашнее задание:повторить теоретический материал; решить задачи (индивидуальные карточки, выбери уровень работы А,Б,В) Молодчина!Ответ верный!
Слайды презентации

Слайд 2 Цели урока:
Обобщить теоретический материал по

Цели урока: Обобщить теоретический материал по теме «Площади» Совершенствовать навыки

теме «Площади»
Совершенствовать навыки решения задач на применение

формул вычисления площадей

Слайд 3 домашнее задание (выбери уровень работы А,Б,В).

План урока:
разминка

домашнее задание (выбери уровень работы А,Б,В). План урока:разминка (проверка теоретических знаний);проверка

(проверка теоретических знаний);
проверка домашнего задания;
проверочный тест;
решение пяти задач с

выбором ответа;

решение пяти задач по готовым чертежам;

самостоятельная работа (4 задачи);

подведение итогов;

дополнительное задание (кроссворд);

Девиз урока:«Незнающие пусть научатся,
а знающие вспомнят еще раз.»

Слайд 4 Правила работы на уроке
По ходу урока заполняются оценочные

Правила работы на урокеПо ходу урока заполняются оценочные листы;В конце урока

листы;
В конце урока подсчитываются баллы;
Тетрадь и оценочный лист сдается

учителю.

Оцени свою работу на уроке:
а) мне было легко;
б) мне было как обычно;
в) мне было трудно.

Слайд 5 Разминка!

Разминка!

Слайд 6 Площади:
S= a h
S= ½ d1d2
S=1/2(a+b)h
S=a2
S=ab
S=1/2d2
S=1/2 ah

Площади:S= a hS= ½ d1d2 S=1/2(a+b)hS=a2S=abS=1/2d2S=1/2 ah

Слайд 7 СЛЕДСТВИЯ
1. S=1/2ab
2. S1:S2= a1:a2, если h1=h2
3. S1:S2=(a1b1):(a2b2),

СЛЕДСТВИЯ1. S=1/2ab2. S1:S2= a1:a2, если h1=h23. S1:S2=(a1b1):(a2b2), если a1۸ b1=

если a1۸ b1= a2۸ b2
4. Медиана треугольника

делит
его на два равновеликих
треугольника.

Слайд 8 Проверка домашнего задания
№481, №474

Проверка домашнего задания№481, №474

Слайд 9 H
Дано: ∆ABC,
BM-медиана
Сравнить:
S∆ABM и S∆BMC
Решение.
Проведем

HДано: ∆ABC, BM-медиана Сравнить: S∆ABM и S∆BMCРешение. Проведем высоту ∆ABM, BH,

высоту ∆ABM, BH, тогда S∆ABM=½AM·BH
Так как BM-медиана ∆ABC, то

AM=MC.
Следовательно, S∆ABM = S∆BMC

№474

Проведем высоту ∆BMC, BH, тогда

SBMC=½MC·BH

Слайд 10 №481
Дано:ABCD –трапеция, ADAB, AB=BC=6см, BCD=135°
Найти: SABCD
Решение
SABCD=½(AD+BC)·AB
Так как

№481Дано:ABCD –трапеция, ADAB, AB=BC=6см, BCD=135° Найти: SABCDРешениеSABCD=½(AD+BC)·ABТак как ADAB, тоHПроведем CHAD

ADAB, то
H
Проведем CHAD и рассмотрим DHC
DHC=9Oº,DCH=CDH=45º,DH=CH.
Так как CH=AB=6см, то

DH=6см,

DA=DH+AH=6+6=12(см)

SABCD=½(12+6)·6=54(см²)





Слайд 11 Теоретический тест
с последующей взаимопроверкой

Теоретический тестс последующей взаимопроверкой

Слайд 12

Слайд 13 ПРОВЕРЬ СЕБЯ !     
       
б
а
в
а
в
а
б
б
в
1 задание
2 задание
3 задание
6

ПРОВЕРЬ СЕБЯ !             бававаббв1 задание2 задание3 задание6 задание4 задание1 задание2

задание
4 задание
1 задание
2 задание
3 задание
4 задание
6 задание
1вариант
2вариант
в
5

задание

б

5 задание

б

Слайд 14 Задача №1
Найти площадь трапеции ABCD
Выбери правильный ответ
a) 144
b)

Задача №1Найти площадь трапеции ABCDВыбери правильный ответa) 144b) 133c) 266d) 19

133
c) 266
d) 19

Слайд 15 Задача №2
Найти площадь параллелограмма ABCD
Выбери правильный ответ
a)20
b)40
c)32
4
5
H

Задача №2Найти площадь параллелограмма ABCDВыбери правильный ответa)20b)40c)3245H

Слайд 16 Задача №3
Найти площадь трапеции ABCD
Выбери правильный ответ
a)36
b)9
c)72
d)63

Задача №3Найти площадь трапеции ABCDВыбери правильный ответa)36b)9c)72d)63

Слайд 17 Задача №4
Найти площадь ромба ABCD.
Выбери правильный ответ
a)80
b)160
c)90
Д

Задача №4Найти площадь ромба ABCD.Выбери правильный ответa)80b)160c)90Д

Слайд 18 Задача №5
Найти площадь треугольника ABC
Выбери правильный ответ
a)112
c)56
14
8
100
50
b)28

Задача №5Найти площадь треугольника ABCВыбери правильный ответa)112c)5614810050b)28

Слайд 19 1.Найти площадь параллелограмма ABCD
H
S=8,1x7=56,7(кв.ед)
7

1.Найти площадь параллелограмма ABCDHS=8,1x7=56,7(кв.ед)7

Слайд 20 2.Найти площадь параллелограмма MNPK
4 см
S=4x5=20(кв.ед)
300

2.Найти площадь параллелограмма MNPK4 смS=4x5=20(кв.ед)300

Слайд 21 3.Найти площадь треугольника ABC
8
450
S=1/2x7x8=28 (кв. ед)

3.Найти площадь треугольника ABC8450S=1/2x7x8=28 (кв. ед)

Слайд 22 4.Найти отношение площадей треугольников
S1: S2=15:14

4.Найти отношение площадей треугольников S1: S2=15:14

Слайд 23 5.Найти площадь трапеции
10
6
S=1/2x(10+22)x6=32x3=96 (кв. ед)

5.Найти площадь трапеции106S=1/2x(10+22)x6=32x3=96 (кв. ед)

Слайд 24 Самостоятельная работа. 1, 2 вариант

Самостоятельная работа. 1, 2 вариант

Слайд 25 Проверь себя!

Проверь себя!

Слайд 26 Вариант 1
1.
5см
10см
S=½·a·h; h=2·5=10(см)
S=½·5·10=25(см2)
Вариант 2
1.
6см
18см
S=½·a·h; h=18:3=69(cм)
S=½·18·6=54(см2)

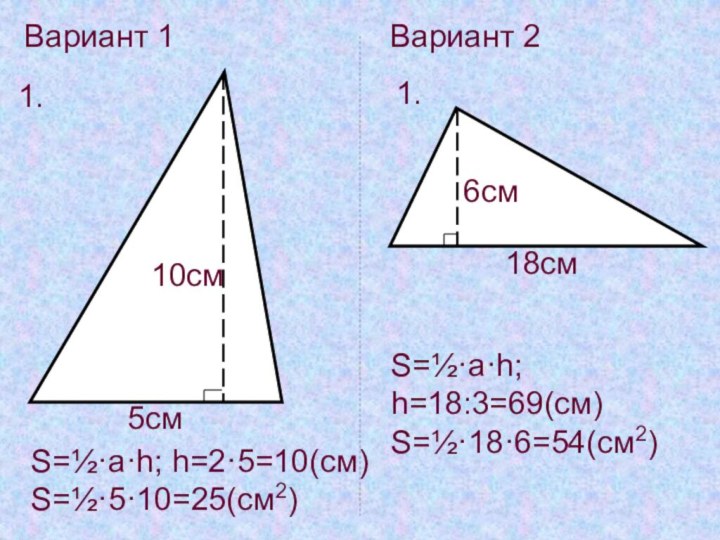
Вариант 11.5см10смS=½·a·h; h=2·5=10(см)S=½·5·10=25(см2)Вариант 21.6см18смS=½·a·h; h=18:3=69(cм)S=½·18·6=54(см2)

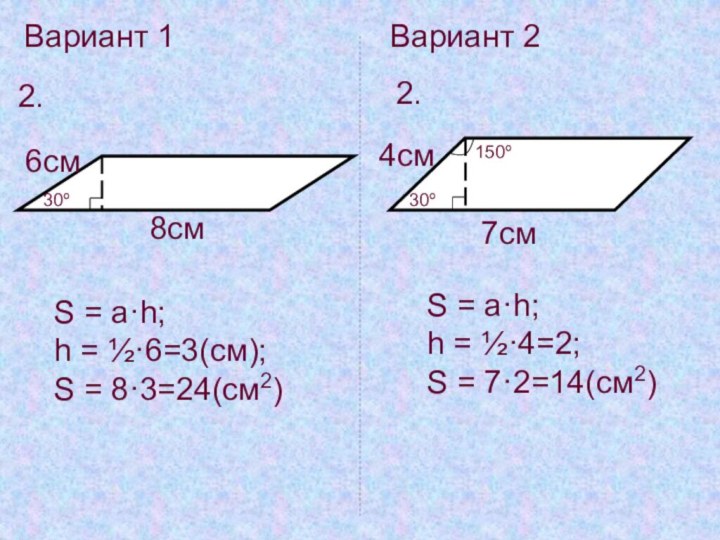
Слайд 27 Вариант 1
Вариант 2
2.
2.
30º
8см
6см
S = a·h;
h = ½·6=3(см);

Вариант 1Вариант 22.2.30º8см6смS = a·h; h = ½·6=3(см); S = 8·3=24(см2)30º150ºS


S = 8·3=24(см2)
30º
150º
S = a·h;
h = ½·4=2;
S

= 7·2=14(см2)

7см

4см

Слайд 28 Вариант 1
Вариант 2
3.
3.
11cм
7cм
45º
S=½·(a+b)·h;
h=4см;
S=½·(11+7)·4;
S=36см2
45º
20cм
6cм
8cм
S=½·(a+b)·h;
h=6см;
b=2O-2·6=8(см);
S=½·(2O+8)·6=84см2

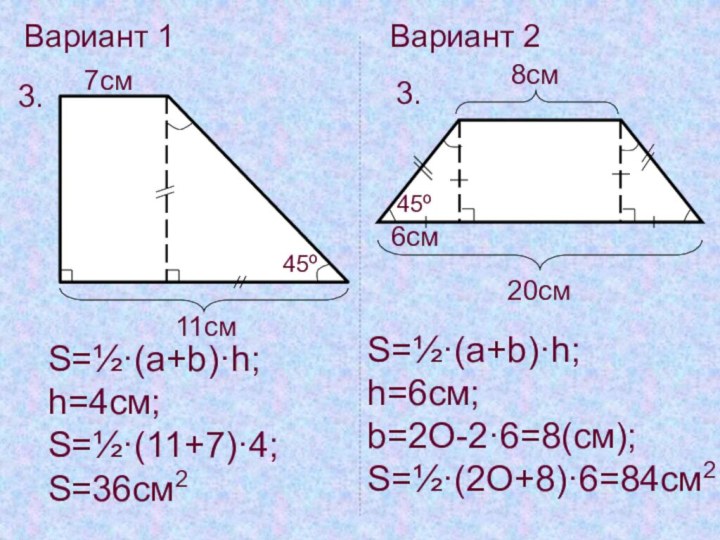
Вариант 1Вариант 23.3.11cм7cм45ºS=½·(a+b)·h;h=4см; S=½·(11+7)·4; S=36см245º20cм6cм8cмS=½·(a+b)·h; h=6см; b=2O-2·6=8(см); S=½·(2O+8)·6=84см2

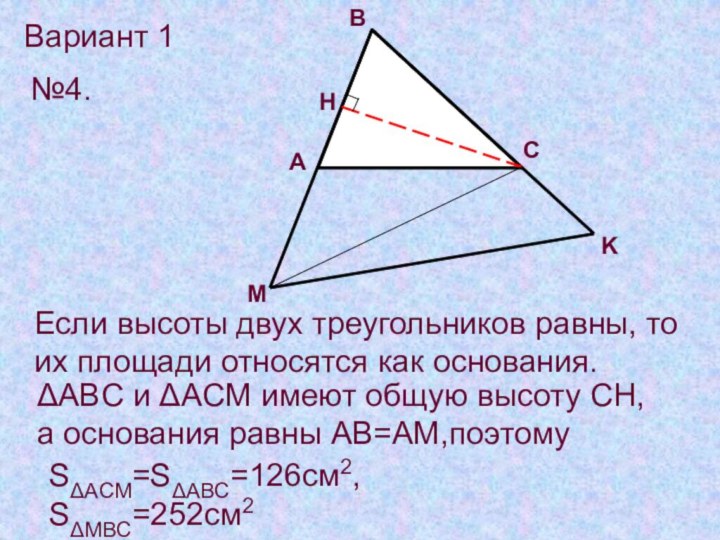
Слайд 29 Вариант 1
№4.
H
Если высоты двух треугольников равны, то
их

Вариант 1№4.HЕсли высоты двух треугольников равны, то их площади относятся как

площади относятся как основания.
ABC и ACM имеют общую высоту

CH,
а основания равны AB=AM,поэтому

SACM=SABC=126см2, SMBC=252см2

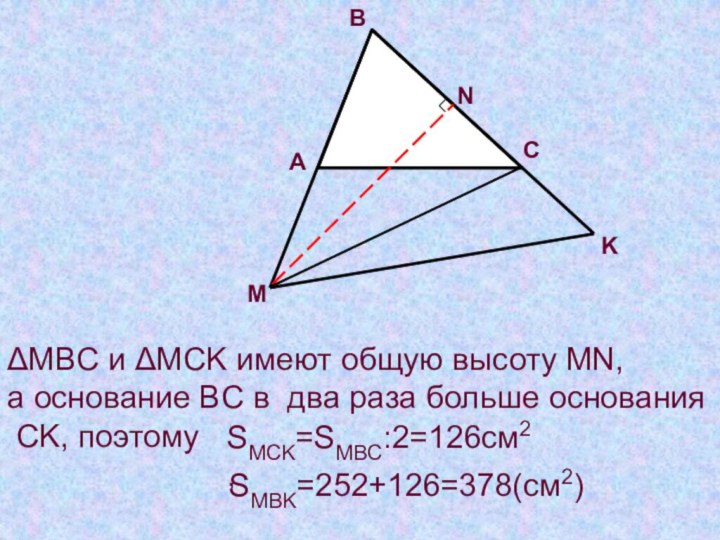
Слайд 30 MBC и MCK имеют общую высоту MN,
а

MBC и MCK имеют общую высоту MN, а основание BC в

основание BC в два раза больше основания
CK,

поэтому

SMCK=SMBC:2=126см2,

SMBK=252+126=378(см2)

N

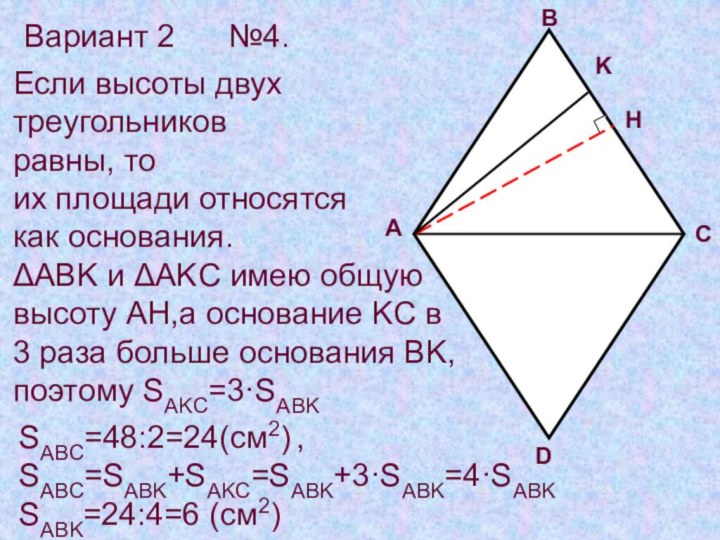
Слайд 31 Вариант 2
№4.
H
K
Если высоты двух
треугольников
равны, то
их

Вариант 2№4.HKЕсли высоты двух треугольников равны, то их площади относятся как

площади относятся
как основания.
ABK и AKC имею общую
высоту

AH,а основание KC в
3 раза больше основания BK,
поэтому SAKC=3·SABK

SABC=48:2=24(см2) ,
SABC=SABK+SAKC=SABK+3·SABK=4·SABK
SABK=24:4=6 (см2)

Слайд 32

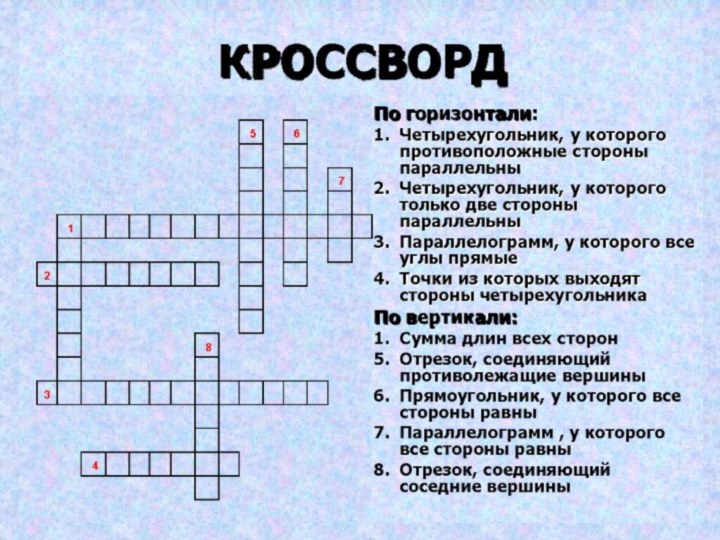
Слайд 33 Проверь себя!
1. Сумма длин всех сторон
5.Отрезок, соединяющий

Проверь себя!1. Сумма длин всех сторон5.Отрезок, соединяющий противолежащие вершины6. Прямоугольник,

противолежащие вершины
6. Прямоугольник, у которого все

стороны равны
7. Параллелограмм , у которого все стороны равны
8. Отрезок, соединяющий соседние вершины

1.Четырехугольник, у которого противоположные стороны параллельны
2. Четырехугольник, у которого только две стороны параллельны.
3. Параллелограмм у которого все углы прямые.
4. Точки, из которых выходят стороны четырехугольника.

Слайд 34 итог

итог урока ОСНОВНЫЕ РЕЗУЛЬТАТЫ

урока ОСНОВНЫЕ РЕЗУЛЬТАТЫ


Мы повторили
Теоретический материал по теме «Площади»
Совершенствовали
Навыки решения задач
Проверили
Свои знания и умения по теме


Слайд 35 Домашнее задание:
повторить теоретический материал;
решить задачи (индивидуальные карточки,

Домашнее задание:повторить теоретический материал; решить задачи (индивидуальные карточки, выбери уровень работы

выбери уровень работы А,Б,В)


Творческое задание:
подготовить презентацию или
сообщение о Пифагоре.

Слайд 36

Слайд 37

Слайд 38

  • Имя файла: tema-ploshchadi-8-klass.pptx
  • Количество просмотров: 153
  • Количество скачиваний: 0
- Предыдущая Презентация по логопедии на тему Осень-весна (1-2 класс)
Следующая - Урок +презентация по обществознанию на тему Что такое дисциплина (7 класс)

Похожие презентации

Презентация по математике на тему Окружность и круг (9 класс) Презентация по математике на тему Окружность и круг (9 класс) 181
Презентация по геометрии на тему Сфера,шар Презентация по геометрии на тему Сфера,шар 149
Презентация по геометрии на тему Вписанные и центральные углы Презентация по геометрии на тему Вписанные и центральные углы 151
Некоторые следствия из аксиом Некоторые следствия из аксиом 161
Трисекция угла Трисекция угла 207
Площадь круга Площадь круга 168
Три признака равенства треугольников Три признака равенства треугольников 133
Курсы по геометрии Курсы по геометрии 133
Свойства равнобедренного Свойства равнобедренного 148
Презентация по геометрии на тему Геометрические фигуры в нашей жизни ученицы 9 класса Презентация по геометрии на тему Геометрические фигуры в нашей жизни ученицы 9 класса 210
Египетский треугольник Египетский треугольник 299
Теорема Пифагора, история, формулировка, доказательства Теорема Пифагора, история, формулировка, доказательства 215
Презентация по математике на тему Сындық нүктелер. Функцияның экстремумдері Презентация по математике на тему Сындық нүктелер. Функцияның экстремумдері 204
Решение задач В4 Решение задач В4 148
Презентация Решение задач по теме Трапеция Презентация Решение задач по теме Трапеция 165
Осевая и центральная симметрия геометрия Осевая и центральная симметрия геометрия 152
Нахождение площадей многоугольников Нахождение площадей многоугольников 149
Признаки параллельности прямых Признаки параллельности прямых 146
Сабақтың тақырыбы: Тік дөңгелек конус, оның элементтері. Конустың жазықтықпен қималары. презентациясы Сабақтың тақырыбы: Тік дөңгелек конус, оның элементтері. Конустың жазықтықпен қималары. презентациясы 380
Презентация по геометрии на тему Тела вращения (тест готовности) Презентация по геометрии на тему Тела вращения (тест готовности) 196
Треугольник, простейший и неисчерпаемый Треугольник, простейший и неисчерпаемый 160
Теорема о трёх перпендикулярах Теорема о трёх перпендикулярах 259
Вневписанная окружность треугольника Вневписанная окружность треугольника 185
Понятие движения Понятие движения 142
Презентация по геометрии 10 класс Двугранный угол Презентация по геометрии 10 класс Двугранный угол 175
Презентация по геометрии на тему: Замечательные точки Презентация по геометрии на тему: Замечательные точки 163
Учебная презентация по теме Аксиома параллельных прямых Учебная презентация по теме Аксиома параллельных прямых 381
Взаимное расположение прямой и окружности Взаимное расположение прямой и окружности 165
Презентация к уроку Площади четырехугольников Презентация к уроку Площади четырехугольников 162
Сравнение отрезков и углов Сравнение отрезков и углов 175