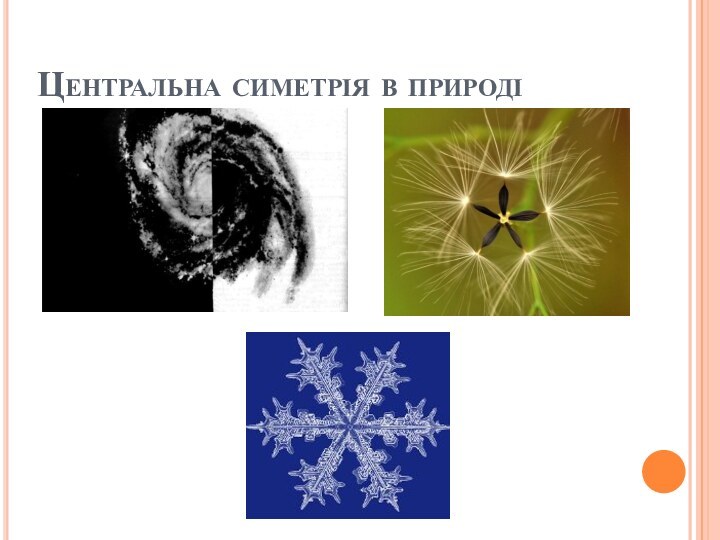
це узгодженість або врівноваженість окремих частин об'єкта,об'єднаних в єдине
ціле, гармонія пропорцій. Симетрія проявляється нетільки в розумінні геометричної будови тіл в природі, але й в ряді областейлюдської діяльності. У мистецтві симетрія може проявитися впропорційності і взаємопВ Епоху Відродження з’явилися
перші фундаментальні дослідження з
теорії перспективи, зокрема роботи
видатних художників Леонардо да Вінчі
(1452-1519) і Альбрехта Дюрера
(1471-1528). Розробником математичних основ теорії проективних перетворень(теорії перспективи) став французький інженер і архітектор Жерар Дезарг (1593-1662).