Презентация на тему 3 к теме урока: Правильные многоугольники.

скромный по численности отряд сумел пробраться в самые глубины

различных наук». Л.Кэрролл

философ Платон, (428 или 427 до н. э. —

348 или 347), одним из девизов своей школы провозгласил: ,, Не знающие геометрии не допускаются!” Правильные многогранники называют также Платоновыми телами. Хотя их знаки пифагорейцы за несколько веков до Платона.

сторон плоскими многоугольниками, называемыми гранями.

Стороны граней – рёбра многогранника,

а концы рёбер – вершины многогранника.

Многогранник называется выпуклым, если он весь расположен по одну сторону от плоскости , каждой из его граней.

Выпуклый многогранник называется правильным, если все его грани – одинаковые правильные многоугольники, в каждой вершине сходится одно и то же число рёбер, а соседние грани образуют равные углы.

Основные понятия.

греческого ,,hedra” – грань) - составлен из четырех равносторонних

треугольников. Каждая его вершина является вершиной трех треугольников. Следовательно, сумма плоских углов при каждой вершине равна 180 градусов.

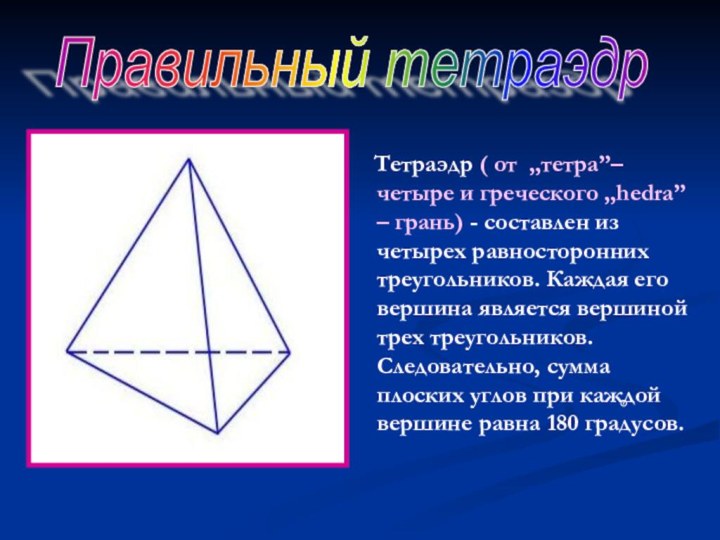
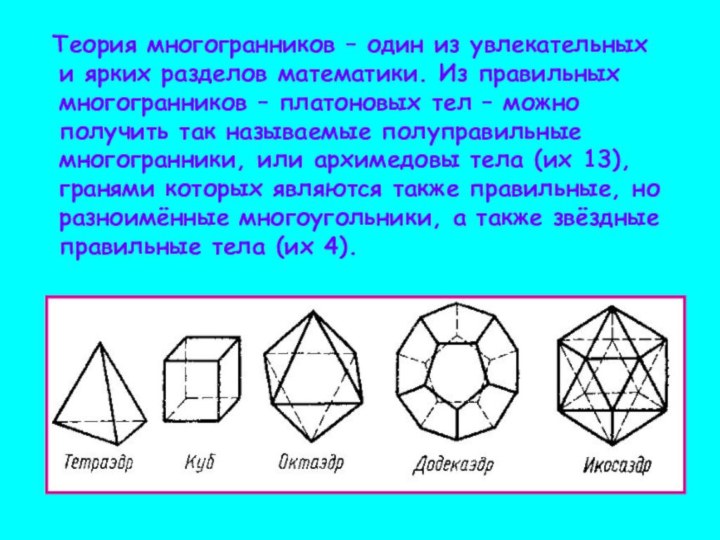
Правильный тетраэдр

восемь и hedra – грань) – составлен из восьми

равносторонних треугольников. Каждая вершина октаэдра является вершиной четырех треугольников. Следовательно, сумма плоских углов при каждой вершине равна 240 градусов.

Октаэдр

и hedra – грань) – составлен из двадцати равносторонних

треугольников. Каждая вершина икосаэдра является вершиной пять треугольников. Следовательно, сумма плоских углов при каждой вершине равна 300 градусов.

Икосаэдр

Каждая вершина куба является вершиной трех квадратов. Следовательно, сумма

плоских углов при каждой вершине равна 270 градусов.

Куб

– двенадцать и hedra – грань) – составлен из

двенадцати правильных пятиугольников. Каждая вершина додекаэдра является вершиной трех правильных пятиугольников. Следовательно, сумма плоских углов при каждой вершине равна 324 градусов .

Додекаэдр

по некоторым рёбрам, а затем развернуть её на плоскости,

то получится фигура, которую называют развёрткой многогранника. На следующем рисунке показано, как можно получить развёртку куба.

разрезы, развёртки могут быть разными.
При изготовлении

моделей многогранников были использованы следующие развёртки.

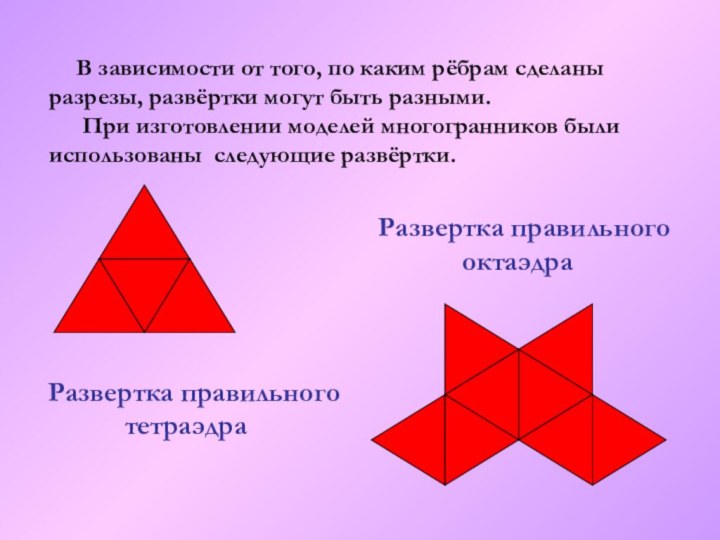
Развертка правильного
тетраэдра

Развертка правильного
октаэдра

додекаэдра

один и тот же результат: В+Г- Р=2. Доказал это

удивительное соотношение один из величайших математиков Леонард Эйлер (1707 – 1783), поэтому формула названа его именем: формула Эйлера.