Презентация на тему по математике Работа с задачами по геометрии на доказательство при подготовке к экзамену.

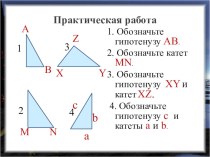
учатся решать задачи на доказательство.
В самом начале процесса подготовки

к экзаменам, на уроках рассматриваются критерии оценивания задач второй части. Например, «Задача по геометрии на доказательство» 0 – 2 балла. Эти критерии применяем в дальнейшей работе. На основе этих критериев строим последующие само- и взаимопроверки.
На слайдах предоставлены несколько заданий: задача и ее решение.
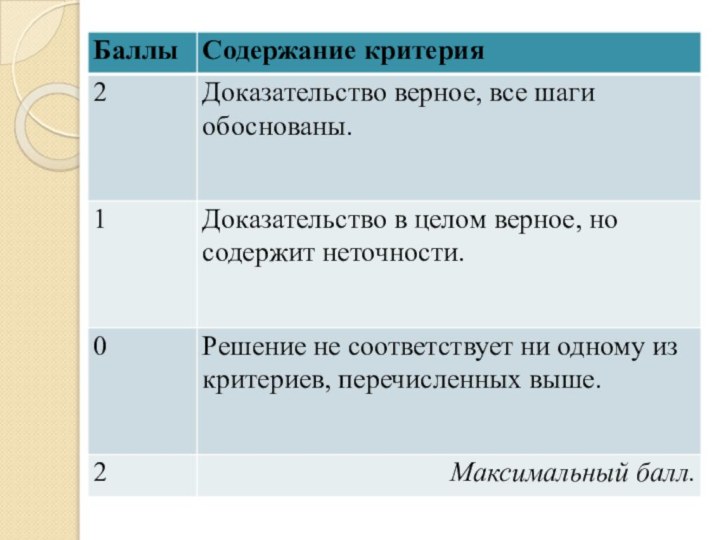
Окружности и их элементы. При разборе предложенного номера многие учащиеся могут поставить 2 балла, но внимательные дети обратят внимание, что задание не выполнено, т.к. нет ответа на поставленный вопрос.
Треугольники, четырехугольники и их элементы. После решения задачи, предлагается проверить чьи-нибудь работы, с обязательным выставлением соответствующих баллов. Для начала можно работать с задачами не очень сложными, постепенно усложняя их, главное в данном случае, что дети учатся самопроверке, самоконтролю, что немаловажно в написании последующего экзамена.
Практика показывает, что после небольшого количества проверенных учащимися работ, ими выдвигается еще один пункт критериев оценивания – это аккуратность написания, возможность прочтения записей.

Треугольники
и их элементы

и их элементы

Четырехугольники
и их элементы

центрами в точках  P и  Q не имеют общих точек, и

ни одна из них не лежит внутри другой. Внутренняя общая касательная к этим окружностям делит отрезок, соединяющий их центры, в отношении a:b.
Докажите, что диаметры этих окружностей относятся как a:b.

NQ - радиус, тогда ∠QNK =90°.
∠PKM = ∠QKN –

вертикальные, значит треугольники PMK и QNK подобные.
Значит PK:QK = PM:QN = MK:KN,
откуда PM:QN = a:b.

центрами в точках  P и  Q не имеют общих точек, и

ни одна из них не лежит внутри другой. Внутренняя общая касательная к этим окружностям делит отрезок, соединяющий их центры, в отношении a:b.
Докажите, что диаметры этих окружностей относятся как a:b.

четырёхугольника ABCD можно описать окружность и что продолжения сторон AD и BC четырёхугольника пересекаются в

точке K. Докажите, что треугольники KAB и KCD подобны.

− ∠ADC = ∠ ABC.
Получаем, что в треугольниках 
KAB и KCD   ∠

ABK =∠ CDK ,  
∠ K -общий,
следовательно, эти треугольники подобны .

что EC=ED. Докажите, что данный параллелограмм — прямоугольник.

как их сумма равна 180°, то углы равны 90°.

Такой параллелограмм — прямоугольник.