- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему О фибоначчи
Содержание
- 2. Попробуйте найти закономерность расположения чисел на этой картинеПеред вами картина московского художника А.Ф. Панкина «Архитектон»
- 3. Последовательность Фибоначчи 1,1,2,3,5,8,13,21,34,55…1 + 1 = 2
- 4. Леонардо Пизанский (Фибоначчи) Фибоначчи родился в
- 5. Леонардо Фибоначчи был величайшим математиком
- 6. Задача о кроликах Сколько пар кроликов,
- 7. Ясно, что если считать первую
- 8. Золотое сечениеЭто такое пропорциональное деление отрезка на
- 9. Число Фибоначчи Ф=1,618
- 10. Некоторые пропорциональные отрезки в теле человека
- 11. Золотое сечение в архитектуре
- 12. Золотое сечение в живой природе
- 13. Золотое сечение в неживой природе
- 14. Скачать презентацию
- 15. Похожие презентации
Попробуйте найти закономерность расположения чисел на этой картинеПеред вами картина московского художника А.Ф. Панкина «Архитектон»













Слайд 2
Попробуйте найти закономерность расположения чисел на этой картине
Перед
вами картина московского художника
А.Ф. Панкина «Архитектон»
Слайд 3
Последовательность Фибоначчи 1,1,2,3,5,8,13,21,34,55…
1 + 1 = 2
1 + 2 = 3
2 + 3 = 5 3 + 5 = 8
5 + 8 = 13
8 + 13 = 21
13 + 21 = 34
21 + 34 = 55
и т.д...
строится по закону:
Каждое число
последовательности равно сумме двух предыдущих
Слайд 4
Леонардо Пизанский (Фибоначчи)
Фибоначчи родился в итальянском
торговом центре городе Пиза, предположительно в 1170-е годы. Его
отец, Гильермо, был торговцем.Леонардо впервые в Европе использовал отрицательные числа, которые рассматривал как долг.
Слайд 5 Леонардо Фибоначчи был величайшим математиком Средневековья.
Всего он написал три значительных математических труда:
Книга абака, опубликованная в 1202 году и переизданная в 1228 году, Практическая геометрия, опубликованная в 1220 году, и Книга квадратур.Труды Леонардо
Слайд 6
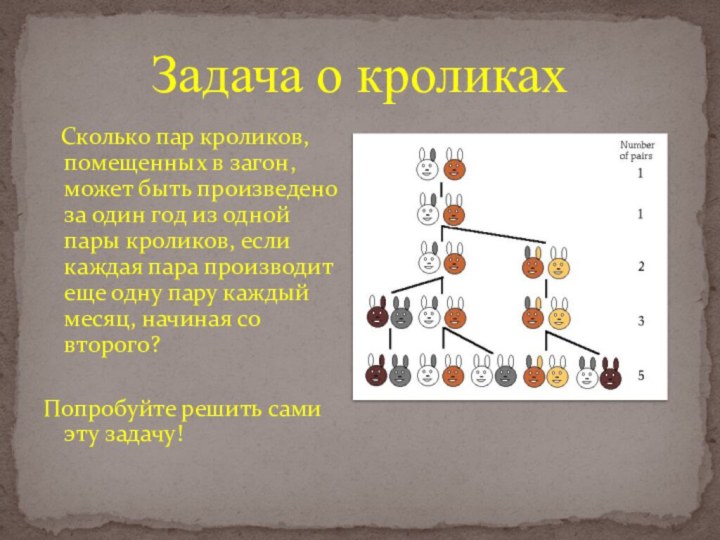
Задача о кроликах
Сколько пар кроликов, помещенных
в загон, может быть произведено за один год из
одной пары кроликов, если каждая пара производит еще одну пару каждый месяц, начиная со второго?Попробуйте решить сами эту задачу!
Слайд 7 Ясно, что если считать первую пару
кроликов новорожденными, то
на 2-й месяц мы будем по-
прежнему иметь одну пару;на 3-й месяц- 1+1=2;
на 4-й- 2+1=3 пары ( из имеющихся пар потомство дает лишь одна пара);
на 5-ый месяц- 3+2=5 пар ( лишь2 родившиеся на 3-й месяц пары дадут потомства на 5-й месяц),
на 6-й месяц – 5+3=8 пар ( потомство дадут только те пары, которые родились на 4-м месяце) и т.д.
Отслеживая каждый месяц количество пар кроликов, получим
последовательность 1;1;2;3;5;8;13;21;34;55;89;144;233;377;…
Ответ: 377 пар.
Проверим решение
Слайд 8
Золотое сечение
Это такое пропорциональное деление отрезка на неравные
части, при котором весь отрезок так относится к большей
части, как сама большая часть относится к меньшейс:b=b:а