Презентация на тему по математике Эвристические приёмы при изучении стереометрии

- методология научного исследования, а также методика обучения, основанная

на открытии или догадке.
Большой Энциклопедический Словарь, в одной из трех трактовок эвристики, определил ее так: «Восходящий к Сократу метод обучения (т.н. сократические беседы)».

французский педагог - математик Лезан "Развитие математической инициативы". В

этой книге эвристический метод не имеет еще современного названия и выступает в виде советов учителю.

Весьма интересна с точки зрения применения эвристического метода в школе книга американского педагога У. Сойера "Прелюдия к математике" .

Дистервег пытался на примере преподавания стереометрии обосновать преимущества эвристического метода. Он пришел к выводу, «что для учащихся гораздо важнее узнать пути к доказательству, нежели само доказательство».

типовых задач используются эвристические правила, которые помогают учащимся в

выполнении правильного построения условия задачи, следовательно, более успешного нахождения решения задачи.

между одной из скрещивающихся прямых и плоскостью, проходящей через

другую прямую параллельно первой, называется расстоянием между скрещивающимися прямыми.

Правило 1. Чтобы найти расстояние между скрещивающимися прямыми, достаточно найти расстояние между параллельными плоскостями, содержащими эти скрещивающиеся прямые.

Правило 2. Чтобы найти расстояние между скрещивающимися прямыми, достаточно найти длину отрезка прямой, перпендикулярной каждой из скрещивающихся прямых, с концами отрезка на данных скрещивающихся прямых.

В единичном кубе АВ…D1 найдите расстояние между прямыми АВ1

и ВС1.

Решение.
Прямые АВ1 и ВС1 скрещивающиеся. Чтобы найти расстояние между ними, достаточно найти расстояние между параллельными плоскостями, содержащими эти прямые. ВС1АD1, так как АВС1D1-параллелограмм. Поэтому ВС1(АB1D1) по теореме о параллельности прямой и плоскости. Точно также АВ1(ВDС1).
Наша задача найти расстояние между параллельными плоскостями (АВ1D1) и (С1DВ). Эти плоскости параллельны по признаку параллельности двух плоскостей.
АВ1DС1, АD1ВС1, АВ1АD1=A, BC1DС1С1 отсюда следует, что (АВ1D1)(С1DВ). Рассмотрим треугольник ОО1С1, где О и О1-точки пересечения диагоналей нижнего и верхнего оснований.△ОО1С1-прямоугольный, так как ОО1 является стороной прямоугольника ОО1С1С. Из вершины О1 треугольника ОО1С1 проведем высоту О1N к гипотенузе ОС1.О1N- искомое расстояние. Докажем это.
О1NОС1, О1NDВ, так как DВ(ОО1С1), отсюда О1N(DBC1), но так как
(АB1D1)(DBC1), то O1N(AB1D1).
Найдем длину О1N из △ОО1С1. O1NOC1OO1O1C1O1NOO1O1C1OC11  

Ответ:

стороной а к плоскости треугольника проведен перпендикуляр AА1, длина

которого равна1. Найти а,
если расстояние между прямыми AC, BA1 равно

Решение
Достроим фигуру ABCА1 до прямой призмы с основаниями АВС и А1В1С1.Прямые АС и ВА1 скрещивающиеся. Рассмотрим △А1ВС1.
АС А1С1, А1С1Є(А1ВС1) отсюда следует, что АС (ВА1С1).
Чтобы найти расстояние между скрещивающимися прямыми АС и ВА1, достаточно найти расстояние между прямой АС и плоскостью (А1ВС1).
Проведем в △АВС медиану ВК. Через точку К проведем прямую KL, параллельную СС1.
△BKL – прямоугольный, BKL90°. В △BKL проведем высоту КР к гипотенузе BL. Докажем, что РК – искомое расстояние. Прямая АС перпендикулярна плоскости (BKL), так как АСВК, АСKL, значит, и перпендикулярна РК, но АС и А1С1 параллельные прямые, поэтому РК перпендикулярно А1С1. Итак, РКBL, PKA1C1, BLA1C1=L,значит, РК(ВА1С1) ч.т.д.
Из△BKL имеем: РК·BL=BK·KL (1), ВК = , KL=1,

BLнайдем из треугольника BKL по теореме Пифагора.
ВL=

подставим данные значения в равенство (1) и найдем значение а.

· = ·1, отсюда а=2
Ответ: 2

ЗАДАЧИ НА НАХОЖДЕНИЕ РАССТОЯНИЯ МЕЖДУ СКРЕЩИВАЮЩИМИСЯ ПРЯМЫМИ.

правильной четырехугольной пирамиде SABCD сторона основания равна 3, а

высота равна 6.Найдите расстояние между медианой АM боковой грани ASB и ребром SD.

Решение.
Проведем медиану АМ. Прямые АМ, SD – скрещивающиеся. Для нахождения расстояния между скрещивающимися прямыми воспользуемся замечанием о нахождении расстояния между скрещивающимися прямыми, то есть найдем расстояние между прямой SD и плоскостью, проходящей через прямую АМ, параллельно прямой SD. Проведем высоту SO пирамиды. В треугольнике SDB проведем среднюю линию МО. МОSD, MOЄ(АСM), отсюда следует, что SD (AMС).Значит, надо найти расстояние между прямой SD и плоскостью (АСМ).
В прямоугольном △SOD проведем высоту ON к гипотенузе DS, докажем, что ON – искомое расстояние. АСDB, SOAC,отсюда следует, что АС(DOS), но ONЄ(DOS), поэтому ONAC,также ONOM (OMDS, ONDS). Значит, ON(AOС) ч.т.д.
Найдем длину отрезка ON. Из △SOD имеем:

ON·DS=DO·SOON= , DO=0,5DB= , SO=6,

DS найдем из△DOS по теореме Пифагора: DS= =

ON= · 6 : = 2.

Ответ: 2.

.
В единичном кубе А…D1 найдите расстояние между прямыми

BA1, DB1.

Решение.
Воспользуемся правилом 2.
Рассмотрим △ A1DB. A1D=DB=A1B△A1DB – равносторонний.
Проведем в нем медиану DP. DPA1B. В △A1BD1 проведем среднюю линию РО. РОA1D1, A1D1A1B, отсюда РОА1В. В △DPO проведем высоту PS к стороне DO. Так как A1BDP, A1BPO,DPPO=P, то A1B(DPO), а, значит, PSA1B, то есть PS – искомое расстояние. PS ·DO=DP·PO DPO Найдем DPO. DPO=(DP2+PO2-DO2)
:(2DP·PO) = .
Действительно, DP= = ,
PO=0,5A1D1=0,5, Do=0,5DB1= , DB1 находим из△DBB1 по теореме Пифагора, DB1= , DPO= = . DPO= .

PS = (DP·PO· DPO):DO=
Ответ :

ПКОЛОСТИ
При нахождении расстояния от данной точки до плоскости удобно

пользоваться следующими эвристическими правилами.
 
Правило 3. Чтобы найти расстояние от данной точки до плоскости, достаточно найти расстояние от произвольной точки одной из параллельных плоскостей, содержащей данную точку, до другой плоскости.

Правило 4. Чтобы найти расстояние от данной точки до данной плоскости, достаточно найти расстояние от произвольной точки прямой, содержащей данную точку, до параллельной ей данной плоскости.

ПКОЛОСТИ
Следующее правило очень часто применяется при решении различных стереометрических

задач.
 
Правило 5. Чтобы доказать, что прямая а, принадлежащая плоскости α, перпендикулярна прямой в, принадлежащей плоскости β, достаточно доказать, что прямая в перпендикулярна плоскости α, тогда прямая в будет перпендикулярна и прямой а.

5.
В единичном кубе А…D1 найдите расстояние от точки

А до плоскости BDC1.
 

Решение.
Чтобы найти расстояние от точки А до плоскости DBC1 воспользуемся правилом 3.
Плоскости (AB1D1), (DBC1) параллельны (см. задачу1). Значит, для решения задачи надо найти расстояние от произвольной точки плоскости (AD1B1) до плоскости (С1ВD), но эта задача решена (см. задачу 1).

6.
В правильной треугольной призме А…С1 все ребра которой равны

1,
Найдите расстояние от точки А до плоскости СА1В1.

Решение.
Чтобы найти расстояние от точки А до плоскости (А1СВ1), достаточно найти расстояние от прямой АВ до этой плоскости., так как прямая АВ параллельна прямой А1В1. △А1СВ1 – равнобедренный, А1С=СВ1, а △АСВ – равносторонний по условию. Проведем в этих треугольниках медианы CN, CK соответственно.△CKN – прямоугольный. АВСК, АВKN, значит АВ (CKN), из вершины К к гипотенузе CN в △CKN проведем высоту КР. КРCN, KPA1B1, так как АВКР и АВ А1В1, а, значит, и А1В1КР, отсюда КР(CА1В1), КР – искомое расстояние. Найдем расстояние КР из △CKN.
KР·NC=KN·KC, KC= , KN=1, NC найдем из
△КСN по теореме Пифагора. NC= ,
KP= · = .
Ответ : .

7.
В основании прямоугольного параллелепипеда лежит квадрат ABCD с площадью

36. Найдите расстояние от точки А1 до плоскости (BC1D), если высота параллелепипеда равна 12.

Решение.
Построим △А1С1О. Он равнобедренный, так как А1О=ОС1. Опустим перпендикуляр A1R на сторону ОС1 треугольникаА1ОС1.Докажем, что А1R – искомое расстояние.
А1RDB. Для доказательства этого факта воспользуемся правилом 5. Докажем, что DBA1R.
DBOC1 (ОС1 – медиана равнобедренного треугольника DBC1,проведенная к основанию). Точно так же DBA1O, значит, DB(A1OC1), но A1R принадлежит плоскости (А1ОС1), поэтому DBA1R.
A1ROC1, A1RDB, DBOC1=О отсюда следует, что A1R (DBC1), то есть А1R – искомое расстояние.
Найдем длину А1R из △А1ОС1.
А1R·OC1=OO1· А1С1 А1R = OO1 ·A1C1:OC1. OO1=12, A1C1=6 , OC1 найдем из треугольника ОСС1 по теореме Пифагора.
ОС1= =9 , A1R=12·6 :9 =8

Ответ: 8.

решении задач на нахождение угла между двумя плоскостями пользуюсь

следующими эвристическими правилами.

Правило 6. Чтобы найти угол между двумя плоскостями, достаточно найти угол между одной из плоскостей и плоскостью, параллельной другой плоскости.

Правило 7. Чтобы найти угол между двумя данными плоскостями, достаточно найти угол между плоскостями, параллельными данным плоскостям.

В правильной четырехугольной призме А…D1 стороны основания равны 2,

а боковые ребра равны 3. На ребре АА1 отмечена точка Е так, что АЕ:ЕА1=1:2. Найдите угол между плоскостями (АВС) и (BED1).

Решение.
Через точку Е проведем плоскость (ЕРК) параллельно плоскости (АВС). Прямая ES – линия пересечения плоскостей (ЕРК) и (BED1).
В△ED1S проведем высоту D1R. D1RES, тогда по теореме о трех перпендикулярах ESRL. D1RL – искомый. Найдем этот угол из △D1RL, D1LR=90°. tgD1RL=D1L:LR,
D1L= · 3=2 , LR найдем из треугольникаELS. LR·ES=QSLE. LR= ,
QS=2, LE=2, ES= по теореме Пифагора из треугольника ESP.

RL= , tgD1RL=2: = ,

D1RL=arctg
Ответ : .

основания правильной треугольной призмы АВС равна а, а высота

– h.Через вершины А, В1 и середину ребра СС1 проведена плоскость. Найдите тангенс угла между этой плоскостью и основанием АВС.

Решение.
Через точку N, где N–середина ребра СС1, проведем плоскость (MNK) параллельно плоскости (АВС). (MKN)(AB1N)=PN. MKAB, B1K=KB отсюда по теореме Фалеса АР=РВ1.
△B1NA – равнобедренный, B1N=AN, тогда NP -высота треугольника, NPAB1; четырехугольник АМВ1К – параллелограмм, так как АМ=В1К и АМВ1К, отсюда МР=РК, но так как △MKN – равносторонний, то МКNP,то есть В1РК – искомый. Из прямоугольного треугольника РКВ1 имеем:
tg В1РК=В1К:РК=0,5h:0,5a= .

Ответ : .

ПЛОСКОСТЬЮ.
В некоторых случаях, чтобы найти угол между прямой и

плоскостью, удобно пользоваться следующими эвристическими правилами.

Правило 7. Чтобы найти угол между прямой и плоскостью, достаточно найти угол между прямой, параллельной данной прямой, и данной плоскостью.
 
Правило 8. Чтобы найти угол между прямой и плоскостью, достаточно найти угол между прямой и плоскостью, параллельной данной плоскости.
 
Правило 9.Чтобы найти угол между прямой и плоскостью, достаточно найти угол между прямой и плоскостью, параллельным данным прямой и плоскости.

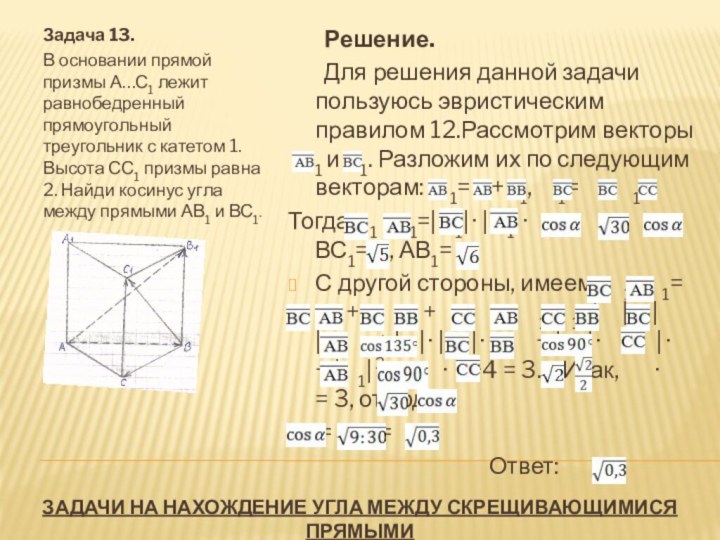
Сторона основания правильной треугольной призмы А…С1 равна 1, высота

равна . Через вершины А, В1 и середину М ребра СС1 проведена плоскость. Найдите синус угла между ребром АС и плоскостью АМВ1.

Решение.
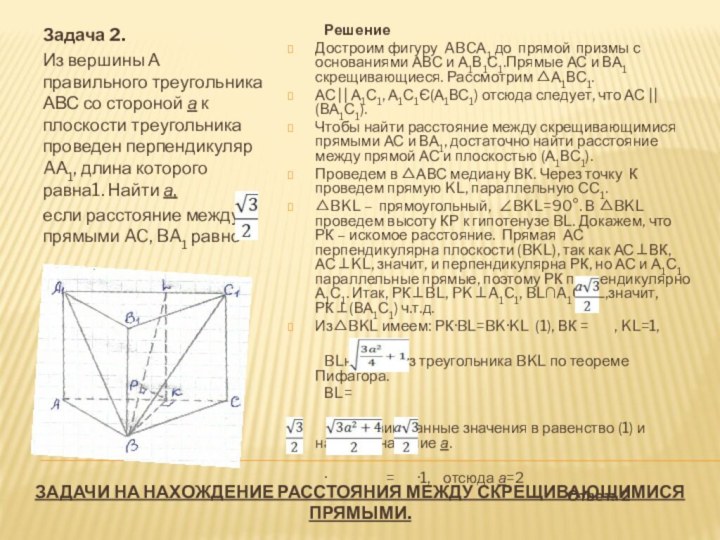
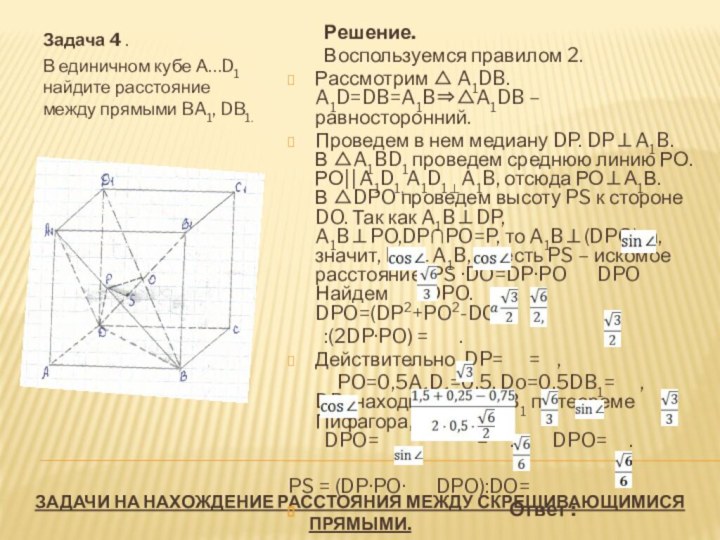
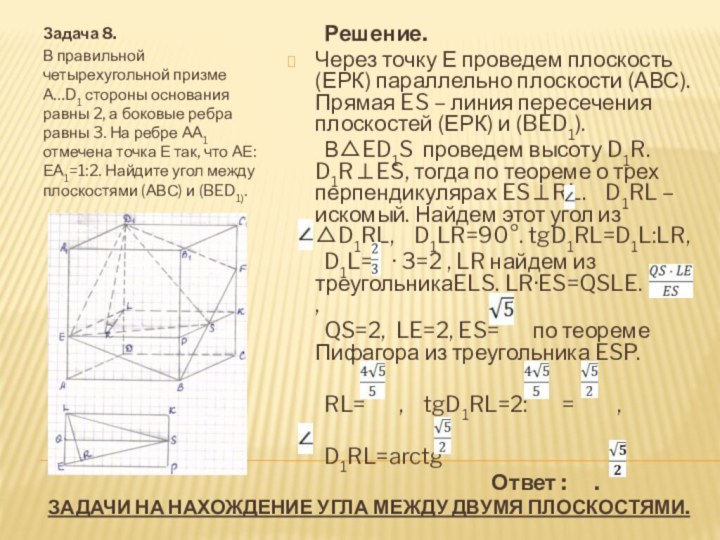
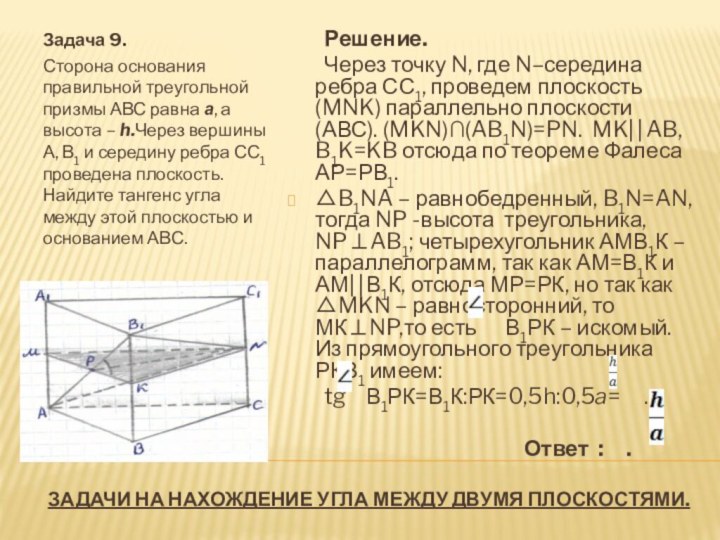
Воспользуемся правилом 9. Через точку Р середину ребра АА1 проведем плоскость С1РК параллельно плоскости МАВ1, РС1АМ, РКАВ1, отсюда (РКС1)(АМВ1).
Рассмотрим угол между С1А1 и плоскостью (С1РК), где С1А1СА.
△С1КР –прямоугольный, так как С1КА1В1, С1КВВ1, отсюда С1К(АВВ1) и, значит, С1КРК. РА1А1С1, РА1А1К, значит, РА1(А1КС1). РА1= , РК=0,5, А1К=0,5.
Нам надо найти угол между прямой А1С1 и плоскостью (РКС1).Так как прямая РА1(А1КС1), то РА1КС1.
Проведем высоту А1S к гипотенузе РК в прямоугольном треугольнике РА1К.
КС1А1К, КС1РА1, отсюда КС1А1S. A1SKC1, A1SPK, отсюда А1S(PKC1), а, значит, A1SSC1, SC1A1 – искомый. A1C1S=A1S:A1C1.

Найдем А1S из △РА1К. А1S·PK=PA1·A1K, A1S= ,
A1C1S= :1= .

Ответ : .

ПРЯМОЙ.
Определение. Длина перпендикуляра, проведенного из точки к прямой называется

расстоянием от этой точки до прямой.
Для нахождения расстояния от точки до прямой удобно применять следующее эвристическое правило. 
Правило10. Чтобы найти расстояние от точки до прямой, достаточно найти расстояние от прямой, параллельной данной прямой и содержащей данную точку, до данной прямой.

В правильной шестиугольной призме А...F1 все ребра которой равны

1, найдите расстояние от точки В до прямой AD1.

Решение.
△ABD1 – прямоугольный, так как прямая АВ перпендикулярна ВD (теорема о трех перпендикулярах), следовательно, перпендикулярна и ВD1.В треугольнике АВD1 из вершины В опустим перпендикуляр ВК на гипотенузу АD1.
ВК – искомое расстояние.
Найдем это расстояние из △ABD1. ВК·АD1=AB·BD1.
AD1 найдем из прямоугольного треугольника ADD1 по теореме Пифагора. Так как AD – большая диагональ основания, то она равна 2а, где а – сторона правильного шестиугольника. AD1= . BD1 найдем из прямоугольного треугольника BDD1 по теореме Пифагора. BD – меньшая диагональ правильного шестиугольника, BD=а . BD= , BD1 = =2, BK=AB·BD1:AD1= .

Ответ : .

правильной шестиугольной призме A…F1 все ребра которой равны 1,

найдите расстояние от точки В до прямой A1F1.

Решение.
Чтобы найти расстояние от точки В до прямой A1F1 достаточно найти расстояние от прямой ВЕ, параллельной A1F1, до прямой A1F1(правило10).
Четырехугольник BEF1A1 – равнобокая трапеция, так как боковые стороны являются диагоналями равных квадратов, а ВЕ, F1A1 – основания, так как FBFA, FAF1A1, а значит, и BEA1F1. Проведем высоту А1К в этой трапеции.А1К – искомое расстояние. Найдем его из треугольника А1ВК по теореме Пифагора.
ВК= (ВЕ-A1F1):2=0,5, A1B= , как диагональ квадрата.

А1К= = = .
Ответ : .

воспользоваться следующим эвристическим правилом.
 
Правило11. Чтобы найти угол между скрещивающимися

прямыми, достаточно найти угол между пересекающимися прямыми, одна из которых данная прямая, другая параллельна второй данной прямой.

Правило12. Чтобы найти угол между скрещивающимися прямыми, достаточно:
а) отложить на этих прямых векторы и ,
б) разложить их по данным векторам,
в) составить их скалярное произведение,
г) найти угол между ними.

основании прямой призмы А…С1 лежит равнобедренный прямоугольный треугольник с

катетом 1.Высота СС1 призмы равна 2. Найди косинус угла между прямыми АВ1 и ВС1.

Решение.
Для решения данной задачи пользуюсь эвристическим правилом 12.Рассмотрим векторы 1 и 1. Разложим их по следующим векторам: 1= + 1, 1= + 1,
Тогда 1 · 1= 1·  1· = · , ВС1= , АВ1=
С другой стороны, имеем: 1· 1= · + · 1 + 1· + 1· 1= ·   +  ·  1· +  1·  · +  12 = - · +4 = 3. Итак, · = 3, отсюда
= = .
Ответ:

основании прямоугольного параллелепипеда А…D1 лежит квадрат, причем его высота

в два раза больше стороны основания. Точка Е – середина ребра СС1. Найдите косинус угла между прямыми ВЕ и АВ1.

Решение
Проведем прямую АК параллельно прямой ВЕ. Чтобы найти косинус угла между прямыми ВЕ и АВ1, достаточно найти косинус угла между прямыми АК и АВ1 ( см. правило 11). 1= ( АК2+АВ12- КВ12) : (2·АК·АВ1)
АВ1 найдем из прямоугольного треугольника АВВ1, АК из прямоугольного треугольника АDK, КВ1 из прямоугольного треугольника КD1B1 по теореме Пифагора. АВ1= а , АК = а , КВ1 = а , 1= (2а2 + 5а2 -3а2) : (2а · а )= .
Ответ: .

способов обучения, который позволяет учащимся проявить творческую активность в

процессе обучения математике, является система эвристических методов и приемов.
При всех достоинствах эвристического обучения оно не является универсальным дидактическим средством, и потому не следует его противопоставлять традиционному обучению. Использование системы средств, методов и приемов эвристического обучения на уроках математики в старших классах средней школы способствуют повышению качества обучения, если:
1) процесс обучения математике реализуется на основе принципов ЭО;
2) разработана и внедрена система эвристических задач в соответствии с видами эвристической деятельности;
3) обоснована и используется на уроках математики система эвристических методов, приемов, средств, способствующая созданию творческой атмосферы и развитию креативных способностей школьников.