ОБЪЕМОМ. Так что же такое – объем пространственной фигуры?
Под объемом пространственной фигуры понимается положительная величина, обладающая следующими свойствами:
равные фигуры имеют равные объемы;
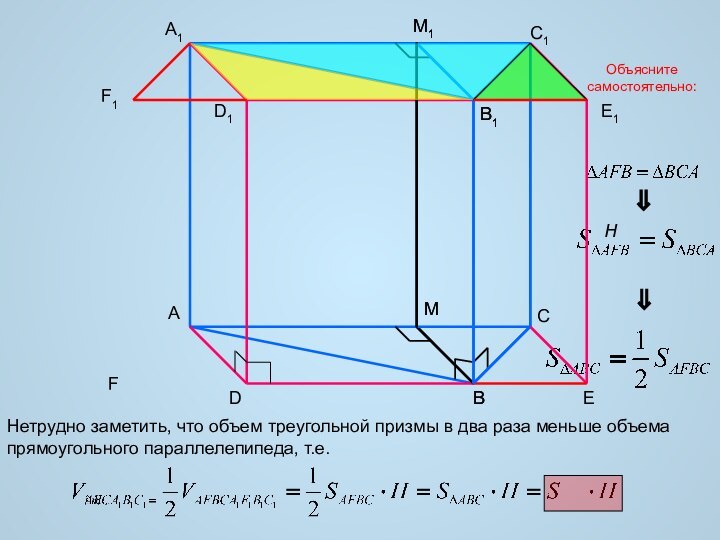
объем фигуры равен сумме объемов ее частей;
объем куба с ребром единичной длины равен одной кубической единице.
V1=V2
V=V1+V2+V3
V=1 куб.ед.






![Объемы фигур ABCB1HA1C1Если применить метод бесконечных интегральных сумм, то получится:xxx∈[ 0; H ]0](/img/tmb/12/1130645/5af3b38ededeae87519ad99073b26b04-720x.jpg)































