Слайд 2
Цели:
Выяснить что такое инверсия;
Увидеть как она применяется при
решении задач на построение;
Как выполнить такое построение;
Дать определение
инверсии, её свойств;
Рассмотреть построения с помощью инверсии.
Слайд 3
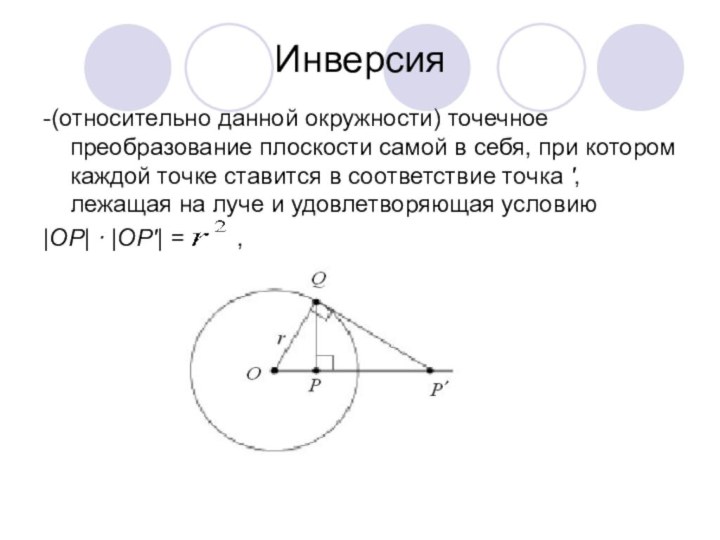
Инверсия
-(относительно данной окружности) точечное преобразование плоскости самой в
себя, при котором каждой точке ставится в соответствие точка
', лежащая на луче и удовлетворяющая условию
|OP| · |OP'| = ,
Слайд 4
Свойства инверсии
Внутренние точки окружности инверсии преобразуются во внешние
и наоборот (поэтому говорят также о зеркальном отображении относительно
окружности); точки самой окружности инверсии остаются неподвижными, то есть преобразуются сами в себя.
Преобразование, обратное для данной инверсии, есть также инверсия, то есть если точка Р переходит при инверсии в точку Р', то одновременно, обратно, точка Р' переходит в точку Р.
Слайд 5
Свойства инверсии
а) Окружности, не проходящие через O, преобразуются
в окружности, не проходящие через O.
б) Окружности, проходящие
через O, преобразуются в прямые, не проходящие через O.
в) Прямые, не проходящие через O, преобразуются в окружности, проходящие через O; прямые, проходящие через O, преобразуются сами в себя.
Слайд 6
Свойства инверсии
Прямая, не проходящая через центр инверсии, преобразуется
в окружность, проходящую через центр инверсии, причём касательная к
этой окружности в центре инверсии параллельна данной прямой.
Прямые, параллельные и не проходящие через центр инверсии, преобразуются в окружности, касающиеся друг друга в центре инверсии и обратно.
Инверсия есть конформное преобразование, то есть при инверсии угол между двумя кривыми в точке их пересечения сохраняется.
При этом, если углы рассматривать как ориентированные, то ориентация углов при применении инверсии изменяется на противоположную.
Слайд 7
Свойства инверсии
Как бы ни были расположены в плоскости
две произвольные окружности, или окружность и прямая, или две
параллельные прямые, всегда можно их преобразовать друг в друга при помощи инверсии, если к инверсии причислить его предельный случай – симметрию относительно прямой.
8. Всякую окружность (или прямую) можно при помощи инверсии преобразовать саму в себя так, чтобы две фиксированные точки этой окружности (или прямой) переходили друг в друга.
При инверсии плоскость, проходящая через центр инверсии (без центра инверсии), преобразуется в себя.
Слайд 8
Свойства инверсии
а) Ортогональные траектории эллиптического пучка окружностей, пересекающихся
попарно в точках A и B, образуют гиперболический пучок
окружностей, имеющий точки A и B предельными точками и прямую AB линией центров.
б) Ортогональные траектории параболического пучка окружностей образуют также параболический пучок окружностей с тем же центром пучка и с линией центров, перпендикулярной к линии центров данного пучка.
в) Ортогональные траектории гиперболического пучка окружностей с предельными точками A и B образуют эллиптический пучок окружностей, попарно пересекающихся в точках A и B.
Слайд 9
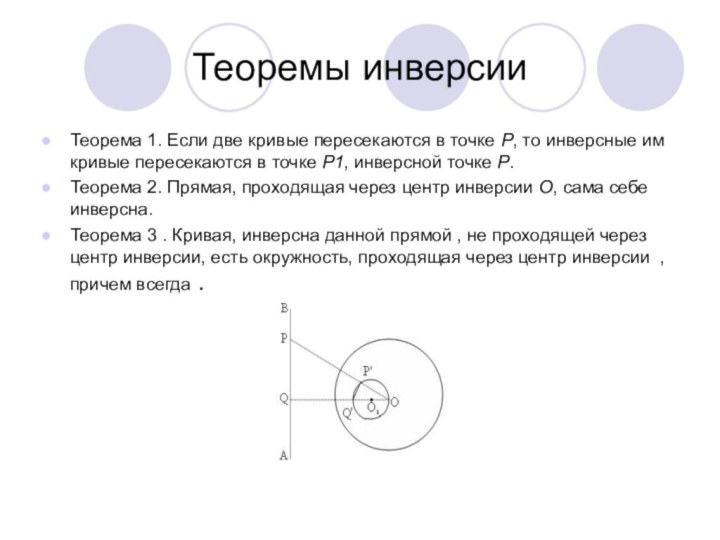
Теоремы инверсии
Теорема 1. Если две кривые пересекаются в
точке P, то инверсные им кривые пересекаются в точке
Р1, инверсной точке Р.
Теорема 2. Прямая, проходящая через центр инверсии О, сама себе инверсна.
Теорема 3 . Кривая, инверсна данной прямой , не проходящей через центр инверсии, есть окружность, проходящая через центр инверсии , причем всегда .
Слайд 10
Свойства инверсии
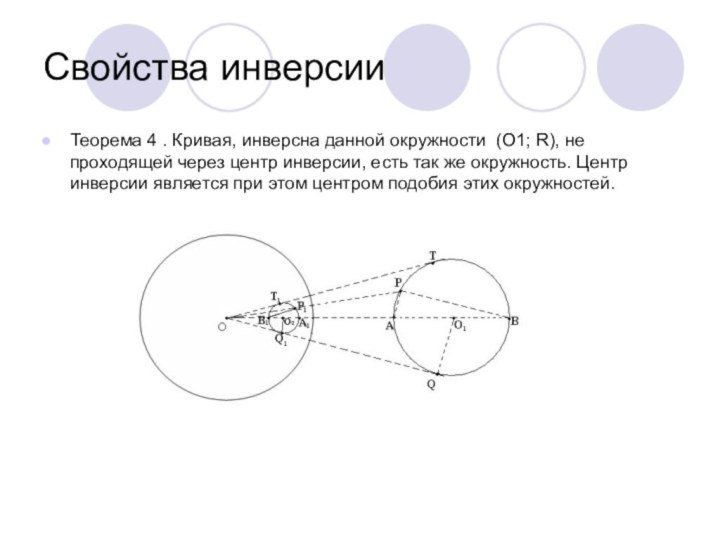
Теорема 4 . Кривая, инверсна данной окружности
(О1; R), не проходящей через центр инверсии, есть так
же окружность. Центр инверсии является при этом центром подобия этих окружностей.
Слайд 11
Практическое применение инверсии
Теорема Мора-Маскерони.
Все построения, выполненные с помощь циркуля и
линейки, могут быть проделаны только с помощью циркуля (при этом мы считаем прямую построенной, если найдены хотя бы две точки этой прямой).
Слайд 12
Практическое применение инверсии
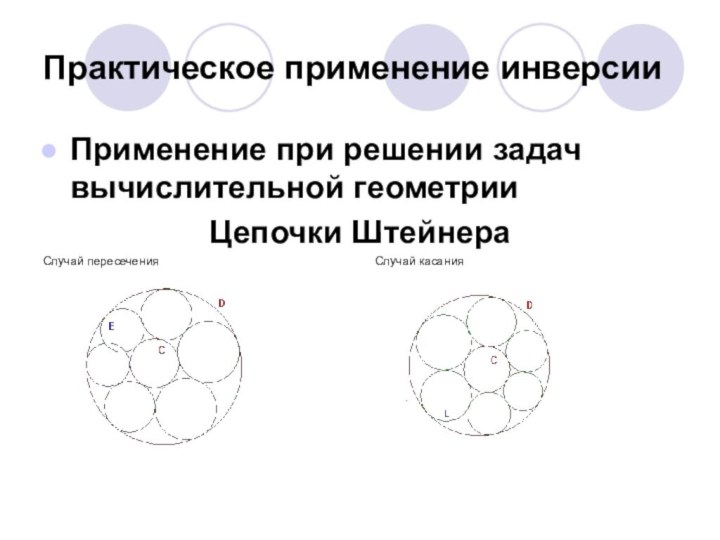
Применение при решении задач вычислительной геометрии
Цепочки
Штейнера
Случай пересечения
Случай касания
Слайд 13
Практическое применение инверсии
С этой цепочкой связано
так называемое утверждение Штейнера (Steiner's porism): если существует хотя
бы одна цепочка Штейнера (т.е. существует соответствующее положение стартовой касающейся окружности, приводящее к цепочке Штейнера), то при любом другом выборе стартовой касающейся окружности также будет получаться цепочка Штейнера, причём число окружностей в ней будет таким же.
Слайд 14
Практическое применение инверсии
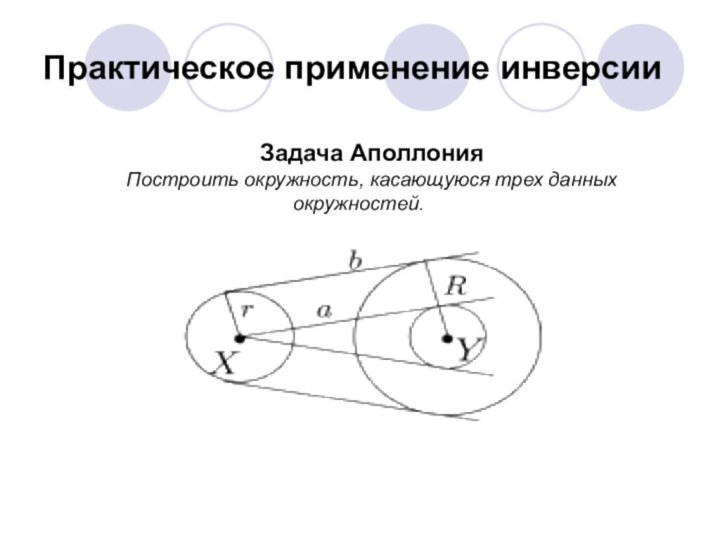
Задача Аполлония
Построить окружность, касающуюся трех данных
окружностей.
Слайд 15
Практическое применение инверсии
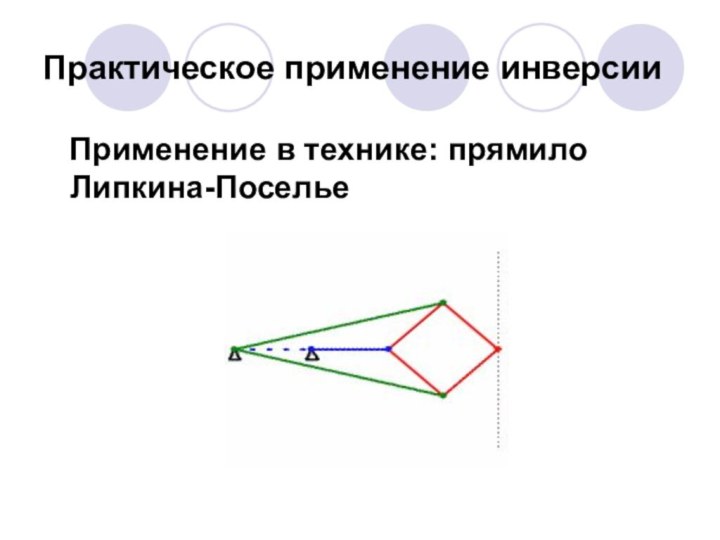
Применение в технике: прямило
Липкина-Поселье