Презентация на тему Радиус вписанной и описанной окружности

от данной точки
на данном расстоянии.
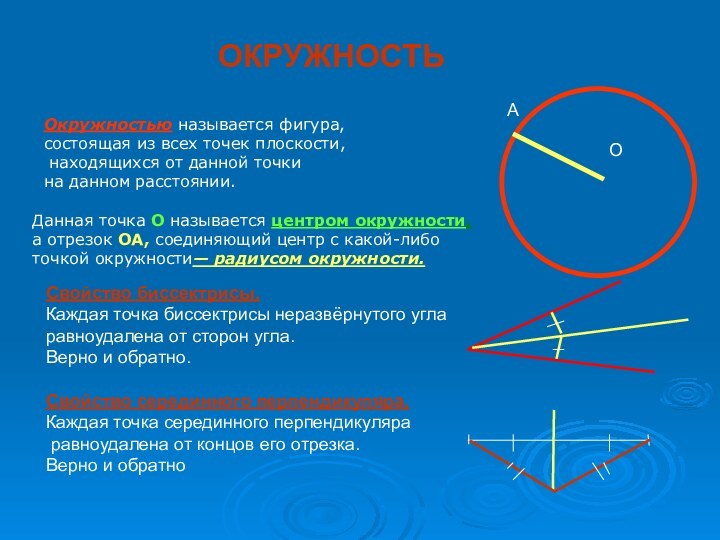
Данная точка O

О

А

Свойство биссектрисы.
Каждая точка биссектрисы неразвёрнутого угла равноудалена от сторон угла.
Верно и обратно.

Свойство серединного перпендикуляра.
Каждая точка серединного перпендикуляра
равноудалена от концов его отрезка.
Верно и обратно

лежит внутри угла и касается его сторон.

 Центр окружности, вписанной

Окружность называется вписанной в выпуклый многоугольник,
если она лежит внутри данного многоугольника  и касается всех прямых,
проходящих через его стороны.

то биссектрисы всех углов данного многоугольника
пересекаются в одной

о

Сам многоугольник в таком случае называется
описанным около данной окружности.
Таким образом, в выпуклый многоугольник можно вписать не более одной окружности.

 
Для произвольного многоугольника невозможно вписать в него и описать около него окружность.

Для треугольника это всегда возможно.

R

O

лежит на серединных перпендикулярах к его сторонам
Окружность называется описанной

Центр описанной окружности около треугольника,
лежит на пересечении серединных перпендикуляров,
проведённых к серединам сторон треугольника

оO

Вокруг любого треугольника можно описать окружность,
и только одну.

a

b

c

R

S - площадь треугольника.

она касается всех трех его сторон,
а её центр

Центр вписанной в треугольник окружности лежит
на пересечении биссектрис внутренних углов треугольника.

В любой треугольник можно вписать окружность, и только одну.

Радиус вписанной в треугольник окружности
равен отношению площади треугольника и его полупериметра

Радиус вписанной окружности




а
с
b
o
r


a
b
c

R
O
Центр описанной

а радиус равен
– половине гипотенузы
- медиане, проведённой к гипотенузе

если суммы противолежащих сторон равны т. е. a +

Верно и обратно
Если окружность вписана в четырёхугольник,
то суммы противолежащих сторон равны
a + c = b + d

Площадь:

r – радиус вписанной окружности

окружность,
если сумма противолежащих углов равна 180°: α +

a

b

c

d

d1

d2

ТЕОРЕМА ПТОЛОМЕЯ
Сумма произведений противолежащих сторон
равна произведению диагоналей: ac + bd = d1 d2

a

b

c

d

ПЛОЩАДЬ ЧЕТЫРЁХУГОЛЬНИКА

где р – полупериметр четырёхугольника

тогда и только тогда,
когда он является прямоугольником;
Радиус

R

d

a

b

В параллелограмм можно вписать окружность тогда и только тогда, когда он является ромбом.
Радиус r вписанной окружности удовлетворяет соотношениям
S=2ar

r

h

d1

d2

a

Около трапеции можно описать окружность тогда
и только тогда, когда эта трапеция — равнобедренная;
Центр окружности лежит на пересечении оси симметрии трапеции с серединным перпендикуляром к боковой стороне

R

АОВ и ДОС прямоугольные (угол О –прямой);
точка О

трапеция

С

многоугольник является вписанным в окружность и описанным около окружности,

Центр правильного многоугольника совпадает
с центрами вписанной и описанной окружностей. 

О

r

R

– радиус описанной окружности;
r – радиус вписанной окружности