н. э. — 190 до н. э.) — древнегреческий математик, один
из трёх (наряду с Евклидом и Архимедом) великих геометров античности, живших в III веке до н. э.Аполлоний прославился в первую очередь
монографией «Конические сечения» (8 книг),
в которой дал содержательную общую теорию
эллипса, параболы и гиперболы.
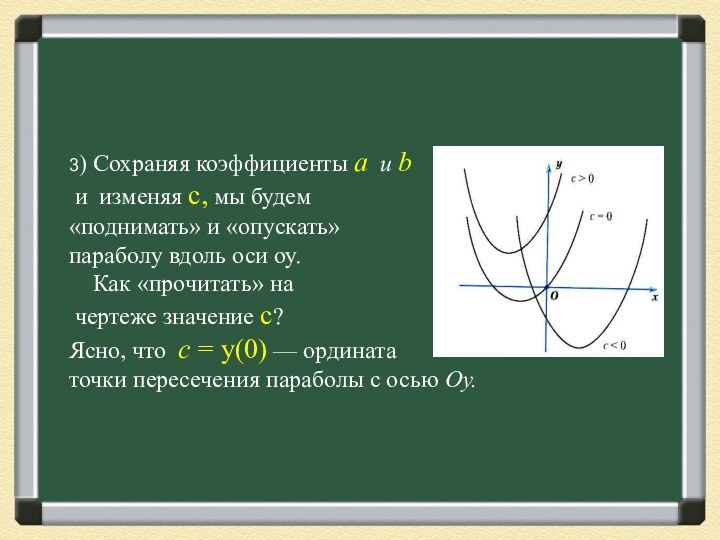
Именно Аполлоний предложил общепринятые
названия этих кривых; до него их называли просто
«сечениями конуса». Он ввёл и другие математические
термины, латинские аналоги которых навсегда вошли
в науку, в частности: асимптота, абсцисса, ордината, аппликата
«Парабола» означает приложение или притча.
Долгое время так называли линию среза конуса, пока не появилась квадратичная функция.