Что такое findslide.org?

FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.

Для правообладателей

Обратная связь

Email: Нажмите что бы посмотреть 

Яндекс.Метрика

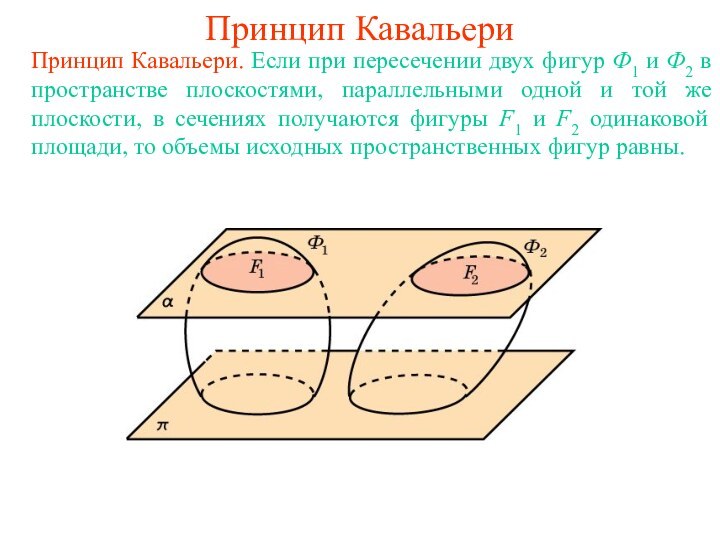
Презентация на тему Принцип Кавальери

Содержание

Объем наклонного цилиндраТеорема. Объем наклонного обобщенного цилиндра равен произведению площади его основания на высоту.
Принцип КавальериПринцип Кавальери. Если при пересечении двух фигур Ф1 и Ф2 в Объем наклонного цилиндраТеорема. Объем наклонного обобщенного цилиндра равен произведению площади его основания на высоту. Объем наклонной призмыСледствие 1. Объем наклонной призмы с площадью основания S и Объем наклонного цилиндраСледствие 2. Объем наклонного кругового цилиндра, высота которого равна h Обобщенный конусПусть F - фигура на плоскости π, и S - точка Упражнение 1Верно ли, что две пирамиды, имеющие общее основание и вершины, расположенные Упражнение 2Верно ли, что любая плоскость, проходящая через центры оснований наклонного кругового Упражнение 3В основаниях наклонной призмы квадраты. Верно ли, что любая плоскость, проходящая Упражнение 4Два цилиндра имеют равные высоты, а площадь основания одного в два Упражнение 5Верно ли, что любая плоскость, проходящая через вершину и центр основания Упражнение 6В основании пирамиды квадрат. Верно ли, что любая плоскость, проходящая через Упражнение 7Два конуса имеют равные высоты, а площадь основания одного в три Упражнение 8Найдите объем наклонной призмы, площадь основания ко­торой равна S, а боковое Упражнение 9Стороны основания параллелепипеда равны 6 дм и 8 дм, угол меж­ду Упражнение 10Найдите объем наклонного параллелепипеда, у которого площадь основания равна Q, а Упражнение 11Найдите объем наклонного кругового цилиндра, радиус основания которого равен R и Упражнение 12Основанием наклонного параллелепипеда служит квадрат, сторона которого равна 1 м. Одно Упражнение 13Основанием наклонной призмы является равносторонний треугольник со стороной a. Одна из Упражнение 14Боковые ребра наклонной треугольной призмы равны 15 см, а расстояния между Упражнение 15Даны три параллелепипеда. Проведите плоскость так, чтобы она разделила каждый параллелепипед
Слайды презентации

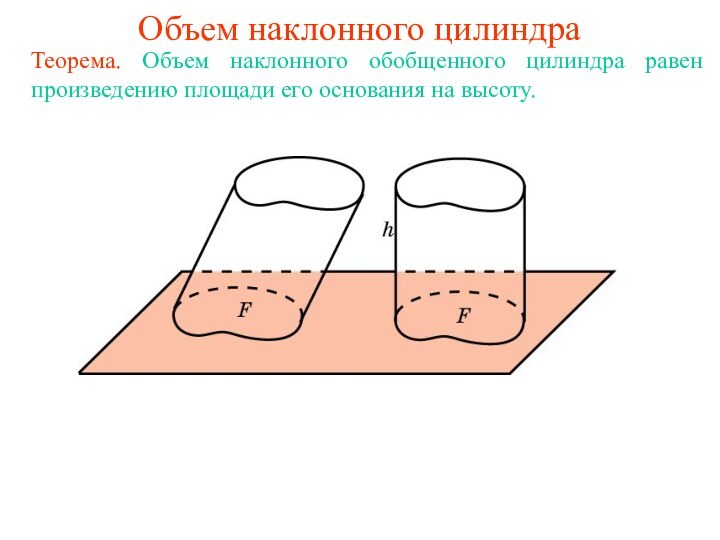
Слайд 2 Объем наклонного цилиндра
Теорема. Объем наклонного обобщенного цилиндра равен

Объем наклонного цилиндраТеорема. Объем наклонного обобщенного цилиндра равен произведению площади его основания на высоту.

произведению площади его основания на высоту.

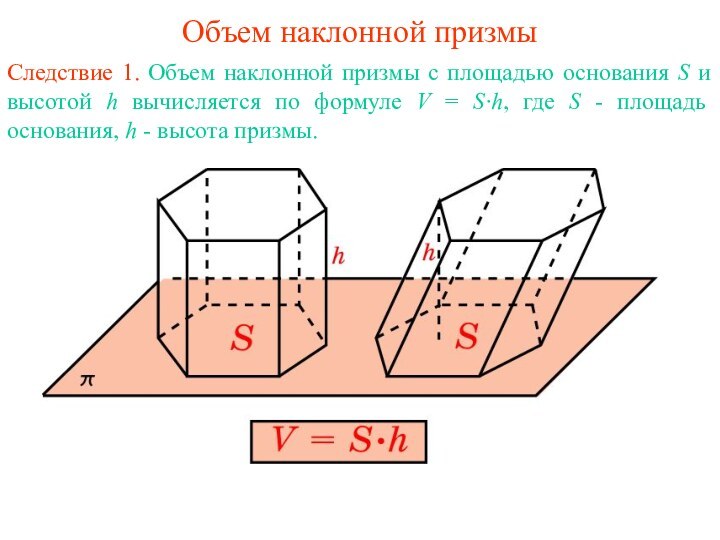
Слайд 3 Объем наклонной призмы
Следствие 1. Объем наклонной призмы с

Объем наклонной призмыСледствие 1. Объем наклонной призмы с площадью основания S

площадью основания S и высотой h вычисляется по формуле

V = S·h, где S - площадь основания, h - высота призмы.

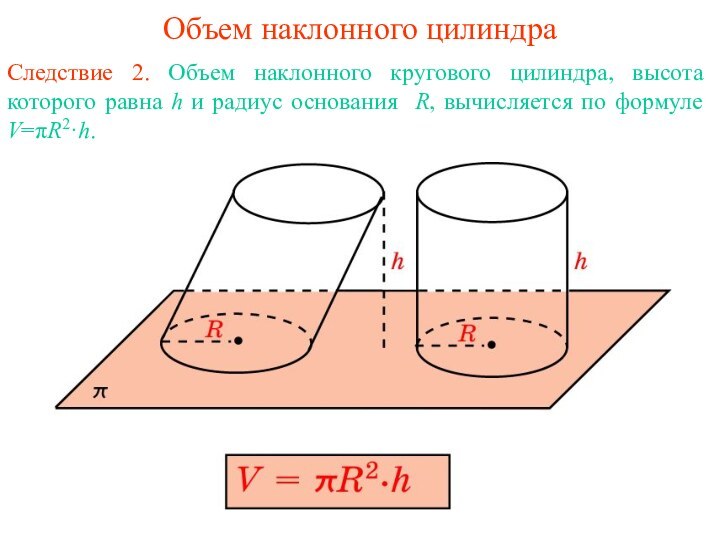
Слайд 4 Объем наклонного цилиндра
Следствие 2. Объем наклонного кругового цилиндра,

Объем наклонного цилиндраСледствие 2. Объем наклонного кругового цилиндра, высота которого равна

высота которого равна h и ради­ус основания R, вычисляется

по формуле V=πR2·h.

Слайд 5 Обобщенный конус
Пусть F - фигура на плоскости π,

Обобщенный конусПусть F - фигура на плоскости π, и S -

и S - точка вне этой плоскости. Отрезки, соединяющие

точки фигуры F с точкой S, образуют фигуру в пространстве, которую мы будем называть обобщенным конусом. Фигура F называется основанием обобщенного конуса, точка S - вершиной обобщенного конуса. Перпендикуляр, опущенный из вершины конуса на плоскость основания, называется высотой обобщенного конуса.

Частным случаем обобщенного конуса является конус и пирамида.

Теорема. Если два конуса имеют равные высоты и основания равной площади, то их объемы равны.

Слайд 6 Упражнение 1
Верно ли, что две пирамиды, имеющие общее

Упражнение 1Верно ли, что две пирамиды, имеющие общее основание и вершины,

основание и вершины, расположенные в плоскости, параллельной основанию, равновелики?
Ответ:

Да.

Слайд 7 Упражнение 2
Верно ли, что любая плоскость, проходящая через

Упражнение 2Верно ли, что любая плоскость, проходящая через центры оснований наклонного

центры оснований наклонного кругового цилиндра, делит его на равновеликие

части?

Ответ: Да.

Слайд 8 Упражнение 3
В основаниях наклонной призмы квадраты. Верно ли,

Упражнение 3В основаниях наклонной призмы квадраты. Верно ли, что любая плоскость,

что любая плоскость, проходящая через центры квадратов, делит призму

на две равновеликие части?

Ответ: Да.

Слайд 9 Упражнение 4
Два цилиндра имеют равные высоты, а площадь

Упражнение 4Два цилиндра имеют равные высоты, а площадь основания одного в

основания одного в два раза больше площади основания другого.

Как относятся их объемы?

Ответ: 2:1.

Слайд 10 Упражнение 5
Верно ли, что любая плоскость, проходящая через

Упражнение 5Верно ли, что любая плоскость, проходящая через вершину и центр

вершину и центр основания наклонного кругового конуса, делит его

на равновеликие части?

Ответ: Да.

Слайд 11 Упражнение 6
В основании пирамиды квадрат. Верно ли, что

Упражнение 6В основании пирамиды квадрат. Верно ли, что любая плоскость, проходящая

любая плоскость, проходящая через вершину пирамиды и центр основания,

делит пирамиду на две равновеликие части?

Ответ: Да.

Слайд 12 Упражнение 7
Два конуса имеют равные высоты, а площадь

Упражнение 7Два конуса имеют равные высоты, а площадь основания одного в

основания одного в три раза больше площади основания другого.

Как относятся их объемы?

Ответ: 3:1.

Слайд 13 Упражнение 8
Найдите объем наклонной призмы, площадь основания ко­торой

Упражнение 8Найдите объем наклонной призмы, площадь основания ко­торой равна S, а

равна S, а боковое ребро b наклонено к плоскости

основания под углом φ.

Ответ: V = S⋅b⋅sin ϕ.

Слайд 14 Упражнение 9
Стороны основания параллелепипеда равны 6 дм и

Упражнение 9Стороны основания параллелепипеда равны 6 дм и 8 дм, угол

8 дм, угол меж­ду ними 45°. Боковое ребро равно

7 дм и наклонено к плоскости основания под углом 45°. Найдите объем параллелепипеда.

Ответ: 168 дм3.

Слайд 15 Упражнение 10
Найдите объем наклонного параллелепипеда, у которого площадь

Упражнение 10Найдите объем наклонного параллелепипеда, у которого площадь основания равна Q,

основания равна Q, а боковое ребро, равное b, наклонено

к плоскости основания под углом φ.

Ответ: Q⋅b⋅sin ϕ.

Слайд 16 Упражнение 11
Найдите объем наклонного кругового цилиндра, радиус основания

Упражнение 11Найдите объем наклонного кругового цилиндра, радиус основания которого равен R

которого равен R и образующая b наклонена к плоскости

основания под углом φ.

Ответ: π⋅R2⋅b⋅sin ϕ.

Слайд 17 Упражнение 12
Основанием наклонного параллелепипеда служит квадрат, сторона которого

Упражнение 12Основанием наклонного параллелепипеда служит квадрат, сторона которого равна 1 м.

равна 1 м. Одно из боковых ребер образует с

каждой прилежащей стороной основания угол в 60° и равно 2 м. Найдите объем параллелепипеда.

Ответ: м3.

Слайд 18 Упражнение 13
Основанием наклонной призмы является равносторонний треугольник со

Упражнение 13Основанием наклонной призмы является равносторонний треугольник со стороной a. Одна

стороной a. Одна из боковых граней перпендикулярна основанию и

является ромбом, у которого меньшая диагональ равна d. Найдите объем призмы.


Слайд 19 Упражнение 14
Боковые ребра наклонной треугольной призмы равны 15

Упражнение 14Боковые ребра наклонной треугольной призмы равны 15 см, а расстояния

см, а расстояния между ними равны 26 см, 25

см и 17 см. Определите объем призмы.

Ответ: 3060 см3.

  • Имя файла: printsip-kavaleri.pptx
  • Количество просмотров: 232
  • Количество скачиваний: 0
- Предыдущая красная книга растений
Следующая - Продовольственная безопасность в Японии

Похожие презентации

Параллелограмм Параллелограмм 159
Фигуры вращения Фигуры вращения 195
Длина отрезка Длина отрезка 183
Презентация по геометрии на тему Симметрия Презентация по геометрии на тему Симметрия 177
обзор аксиоматик геометрии обзор аксиоматик геометрии 170
ОБЪЁМНЫЕ ТЕЛА И МНОГОГРАННИКИ. ОБЪЁМНЫЕ ТЕЛА И МНОГОГРАННИКИ. 188
Презентация к интегрированному уроку Геометрия и русский язык Презентация к интегрированному уроку Геометрия и русский язык 157
Свойства пирамиды с равными боковыми ребрами Свойства пирамиды с равными боковыми ребрами 154
Презентация по геометрии Простейшие задачи в координатах (9 класс) Презентация по геометрии Простейшие задачи в координатах (9 класс) 147
шар цилиндр конус шар цилиндр конус 152
Число Пи Число Пи 183
Презентация для итогового повторения . Окружность. Длина окружности. Площадь круга Презентация для итогового повторения . Окружность. Длина окружности. Площадь круга 175
Презентация по геометрииисследование геометрических форм кибитки и джолума Презентация по геометрииисследование геометрических форм кибитки и джолума 157
Презентация по геометрии Математический диктант Четырехугольники (8 класс) Презентация по геометрии Математический диктант Четырехугольники (8 класс) 184
Презентация ашық сабақ тақырыбы: Квадрат теңдеу түбірлері Презентация ашық сабақ тақырыбы: Квадрат теңдеу түбірлері 163
Задачи в координатах Задачи в координатах 188
Презентация по математике на тему Биссектриса угла (7 класс) Презентация по математике на тему Биссектриса угла (7 класс) 195
Геометрия пирамида Геометрия пирамида 163
Центральная симметрия Центральная симметрия 173
Числа и точки на прямой Числа и точки на прямой 154
Многоугольники. Решение задач Многоугольники. Решение задач 173
Изображение куба, описанного около сферы Изображение куба, описанного около сферы 146
Цветы из сада геометрии Цветы из сада геометрии 209
Мир невозможных фигур Мир невозможных фигур 205
детали детали 177
Признаки равенства треугольников (обобщающий урок) Признаки равенства треугольников (обобщающий урок) 224
Понятие цилиндра Понятие цилиндра 165
Теорема Пифагора Теорема Пифагора 151
Симметрия правильных многогранников Симметрия правильных многогранников 188
Осевая и центральная симметрия геометрия Осевая и центральная симметрия геометрия 152