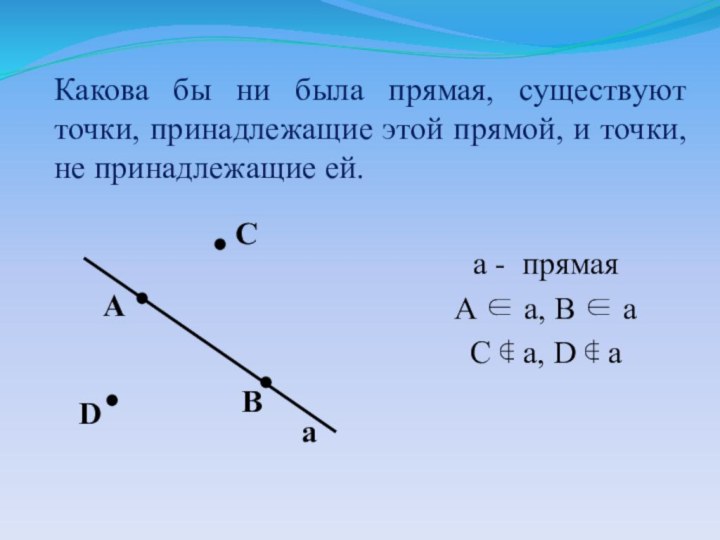
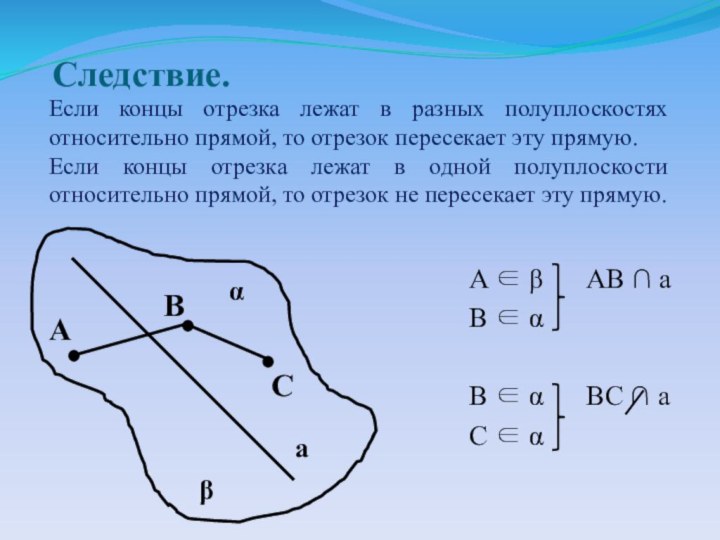
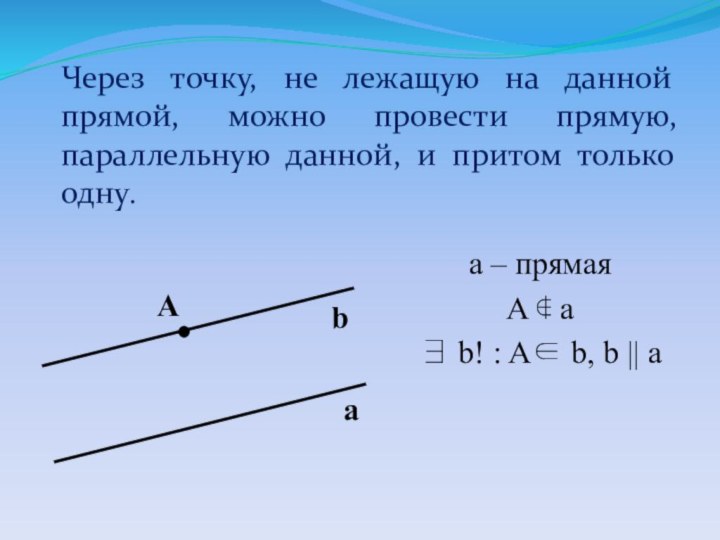
этой прямой, и точки, не принадлежащие ей.
a - прямая
A
a, B aC a, D a
D
C
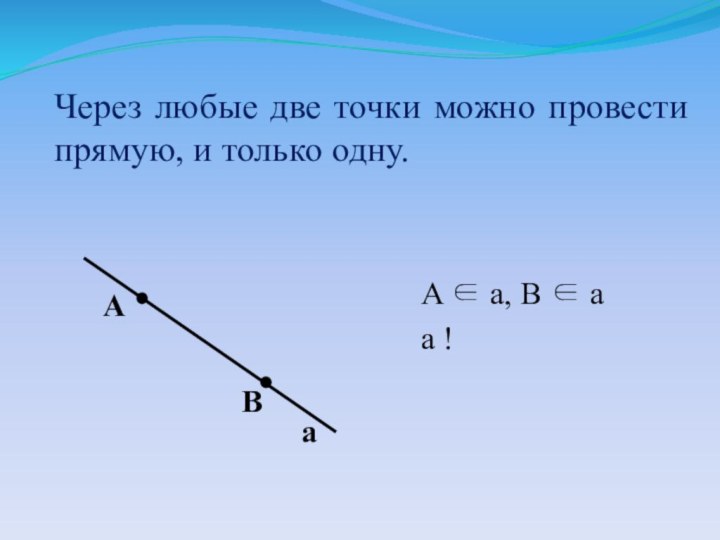
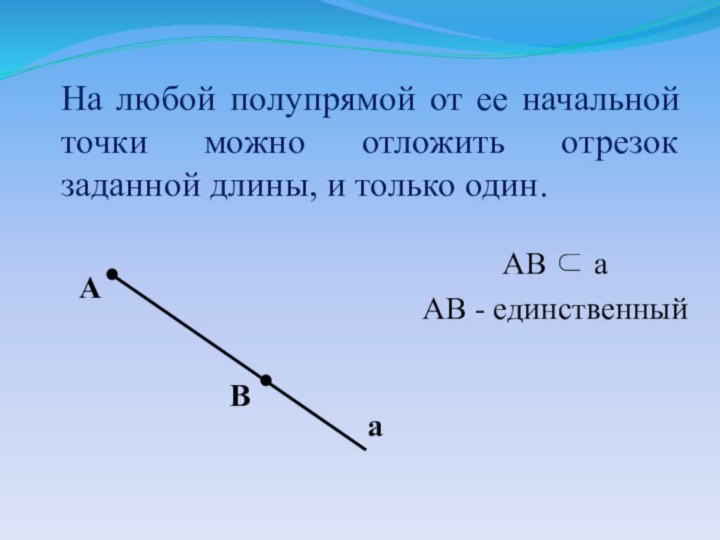
A
B
a
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Email: Нажмите что бы посмотреть










D
C
A
B
a
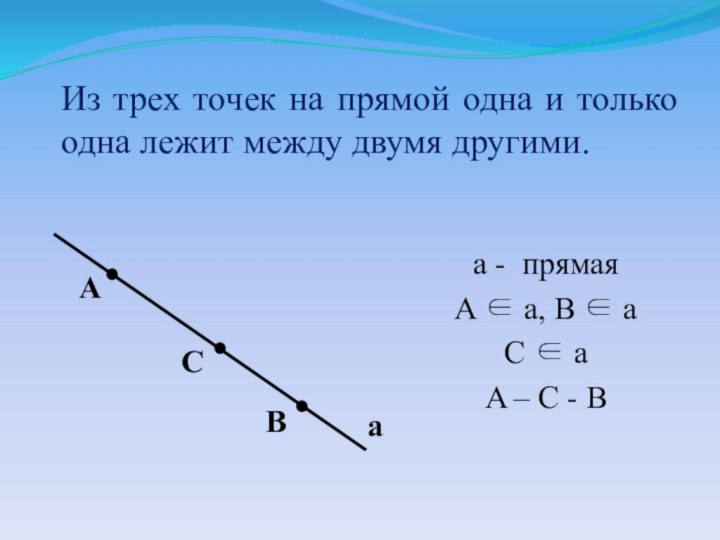
C
A
B
a
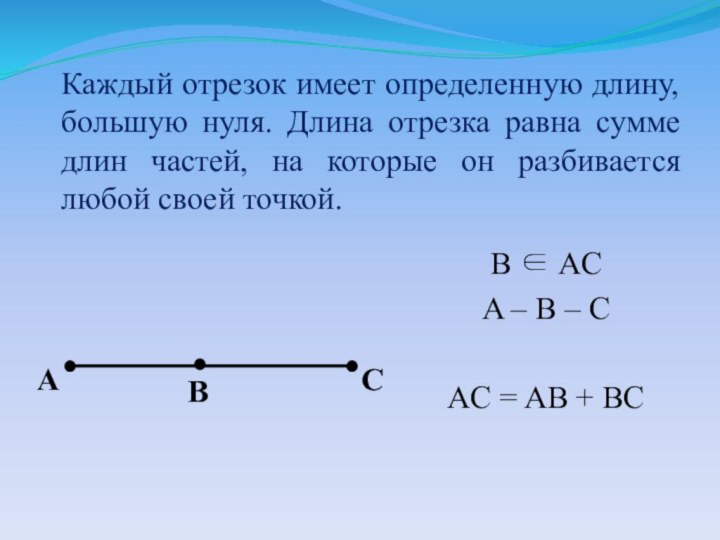
B AC
A – B – C
AC = AB + BC
C
A
B
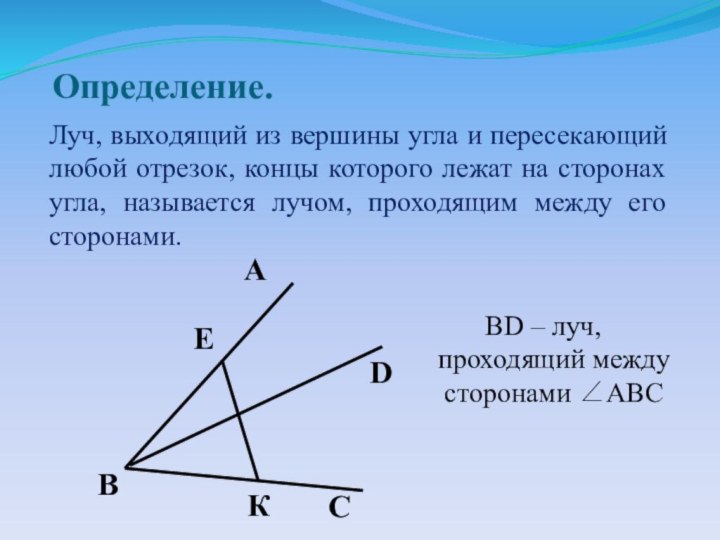
BD – луч, проходящий между сторонами ABC
ABC = ABD + DBC
C
A
B
D
Е
К
BD – луч, проходящий между сторонами ABC
A AB ∩ a
B
B BC ∩ a
C
a
C
A
B
A
B
a
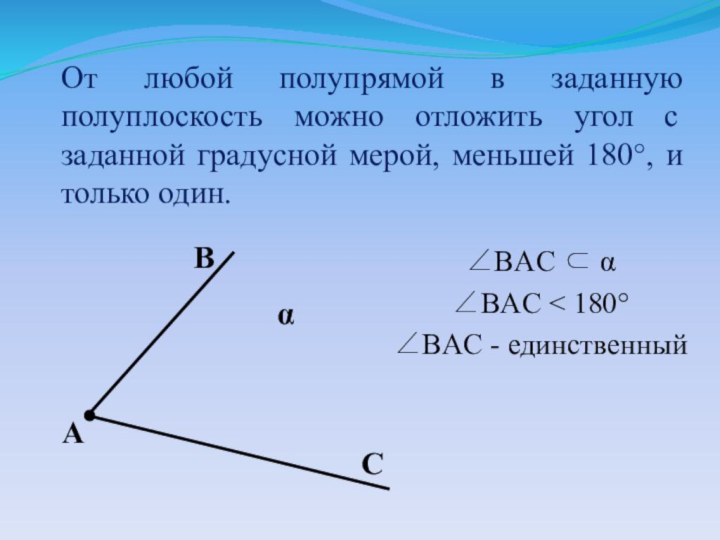
BAC
BAC < 180
BAC - единственный
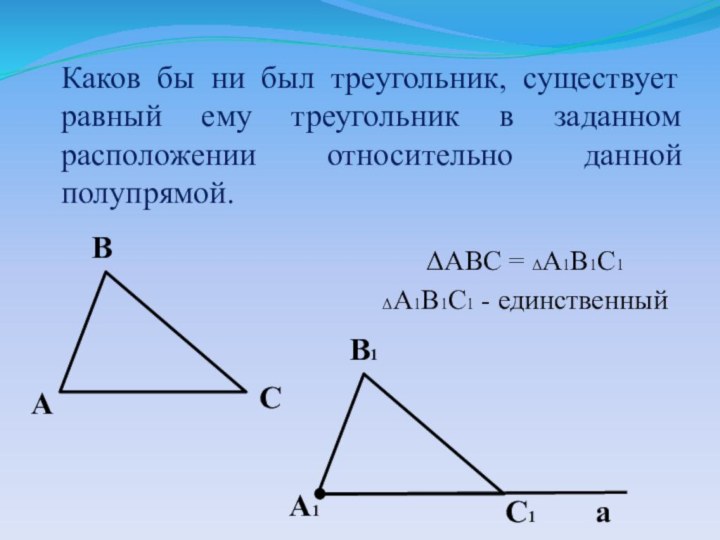
С
С
a
B
A
С1
B1
A1