Слайд 2
Цель:
.изучить применение «золотого сечения» в Мировой архитектуре и
архитектуре города Белгорода.
Объект исследования - скульптурные и архитектурные сооружения
города Белгорода.
Предмет исследования – «золотое сечение», применение его принципов в архитектуре.
Задачи:
Изучить литературу по данной теме;
Проанализировать пропорцию как математическую закономерность;
Выявить в «золотом сечении» - гармоническую пропорцию;
По фотографиям изучить применение «золотого сечения» в архитектуре города Белгорода.
Актуальность:
Убедится в закономерности «золотого сечения»;
Доказать его применение и в наше время при постройке зданий и памятников культуры
Слайд 3
Методы исследования:
Теоретический ( определялась основная закономерность образования «Золотого
Сечения», проводилось математическое описание выявленной закономерности.
Аналитический ( проводился анализ
выявленной закономерности «Золотого Сечения».
Практический ( применение выявленного ряда закономерностей «Золотого Сечения» в новых измененных ситуациях.
Измерительные работы и расчеты.
Анализ полученных результатов.
Слайд 4
Замечательный советский зодчий И.В. Жолтовский (1867-1959) считал ,
что гармония в природе и гармония в архитектуре обретают
одинаковое математическое выражение в законе золотого сечения.
Слайд 5
Пропорциональность является наиболее ярким, зримым, закономерным выражением архитектурной
гармонии. Пропорция - это математическая закономерность, прошедшая через душу
зодчего, это поэзия числа и геометрии в его архитектурном языке. Вот почему на языке пропорций говорили зодчие всех времен и всех архитектурный направлений: древние египтяне и древние греки, средневековые каменотёсы и древнерусские плотники, представители борокко и классицизма и т.д.
Слайд 6
Многочисленные исследования показали, что на точке золотого сечения
обычно бывает кульминация в поэтических, драматургических и музыкальных произведениях.
Золотое сечение мы находили в общей композиции произведения и в соответствии его частей не менее удивительно и то, что золотое сечение мы находим всегда,в совершенно различных цивилизациях, отделенных друг от друга тысячелетиями: в усыпальнице Хеопса в Древнем Египте и в храме Парфенон в Древней Греции и в храме Покрова на Нерли. Золотое сечение мы обнаруживаем и в музыкальных шедеврах Баха, Моцарта, Вагнера, Шопена, Глинки и в поэтических произведениях от Лермонтова до Вознесенского.
Слайд 7
Геометрия владеет двумя сокровищами : одно из них
– это теорема Пифагора, а другое деление отрезка в
среднем и крайнем отношении… Первое можно сравнить с мерой золота, второе же больше напоминает драгоценный камень.
И. Кеплер
Слайд 8
Слово «пропорция» ввел в употребление Цицерон в первом
веке до н.э., переведя на латынь - «аналогия», который
буквально означал «вновь-отношение», или, как мы говорим, «соотношение». С тех пор вот уже 2000 лет пропорцией в математике называют равенство между отношениями четырех величин a, b, c, d a / b = c / d.
Слайд 9
Пропорция в искусстве
Пропорция в искусстве определяет соотношение величины
элементов художественного произведения , либо соотношение отдельных элементов и
всего произведения в целом.
Возьмём простой пример: деление отрезка прямой. Если отрезок разделить пополам, зеркально- симметрично, то такое деление выглядит уравновешенным, мертвым.
Скорее всего золотая пропорция была заимствована Пифагором у древних египтян, которые знали её задолго до Пифагора и которых он посетил в своих странствиях по свету.
Слайд 10
Золотая пропорция определяется как деление отрезка на две
неравные части, при котором меньшая из них так относится
к большей, как последняя ко всей длине отрезка.
Будучи мерой, законом природы, золотое сечение становится и мерой человеческого творчества , «законом красоты»: совершенная природа даёт человеку образец совершенства.
Золотое сечение мы находим всюду: в изобразительном и прикладном искусстве, в архитектуре и музыке, в литературе, в предметах быта и машинах.
Слайд 11
Золотое сечение- гармоническая пропорция
В математике пропорцией (лат. proportio)
называют равенство двух отношений:
a : b = с :
d.
Отрезок прямой AB можно разделить на две части следующими способами:
На две равные части – AB : BC= AB: BC
На две неравные части в любом отношении (такие части пропорции не образуют)
Таким образом, когда AB : BC = AC : BС
Последнее и есть золотое деление или деление отрезка в крайнем или среднем отношении.
Слайд 12
Деление отрезка прямой по золотому сечению.
Из точки
B восставляется перпендикуляр, равный половине AB. Полученная точка С
соединяется линией с точкой A. На полученной линии откладывается отрезок BC, заканчивающийся точкой D. Отрезок AD переносится на прямую AB. Полученная при этом точка E делит отрезок AB в соотношении золотой пропорции.
Отрезки золотой пропорции выражаются бесконечной иррациональной дробью AE= 0,618…, если AB принять за единицу, BE= 0,382…, Для практических целей часто используют приближенные значения 0,62 и 0,38. Если отрезок AB принять за 100 частей, то большая часть отрезка равна 62, а меньшая- 38 частям.
Решение этого уравнения:
Свойства золотого сечения описываются уравнением:
Х2 –Х - 1=0
Слайд 13
Ряд Фибоначчи
Фибоначчи (Леонардо из Пизы) (1170 – 1250)
Итальянский
математик-монах. Он много путешествовал по Востоку, познакомил Европу с
арабскими цифрами. В 1202 г. вышел в свет его математический труд «Книга об абаке» (счетной доске), в которой были собраны все известные на то время задачи. Фибоначчи так же занимался решением практических нужд торговли.
Слайд 14
Одна из задач « Книги об абаке» гласила
« Сколько пар кроликов в один год от одной
пары родится» . Размышляя на эту тему, Фибоначчи выстроил такой ряд цифр:
Слайд 15
Ряд чисел 0,1,2,3,5,8,13,21,34,55 и т. д, известен как
ряд Фибоначчи. Особенность последовательности чисел состоит в том, что
каждый её член, начиная с третьего, равен сумме двух предыдущих 2+3=5; 3+5=8; 5+8+13; 8+13=21; 13+21+34 и т. д., а отношение смежных чисел ряда приближается к отношению золотого деления. Так, 21 : 34=0,617, а 34:55=0,618. Это отношение обозначается символом Ф. Только это отношение – 0,618: 0,382- даёт непрерывное деление отрезка прямой в золотой пропорции, увеличение его или уменьшение до бесконечности, когда меньший отрезок так относится к большему, как большой ко всему.
Слайд 16
Принципы формообразования в природе.
Раковина закручена по спирали. Если
её развернуть, то получится длина, немного уступающая длине змеи.
Небольшая десятисантиметровая раковина имеет спираль длиной 35 см. Спирали очень распространены в природе. Представление о золотом сечении будет неполным, если не сказать о спирали.
Слайд 17
Среди придорожных трав ничем не примечательное растение- цикорий.
Если приглядеться, то можно увидеть, что от основного стебля
образовался отросток. Тут же расположился первый листок.
Отросток делает сильный выброс в пространство, останавливается, выпускает листок, но уже короче первого, снова делает выброс в пространство, но уже меньшей силы, выпускает листок ещё меньшего размера и снова выброс. Если первый выброс принять за 100 единиц, то второй равен 62 единицам, третий – 38, четвертый- 24 и т. д. Длина лепестков тоже подчинена золотой пропорции. В росте, завоевании пространства растение сохранило определенные пропорции. Импульсы его роста постепенно уменьшались в пропорции золотого сечения.
Слайд 18
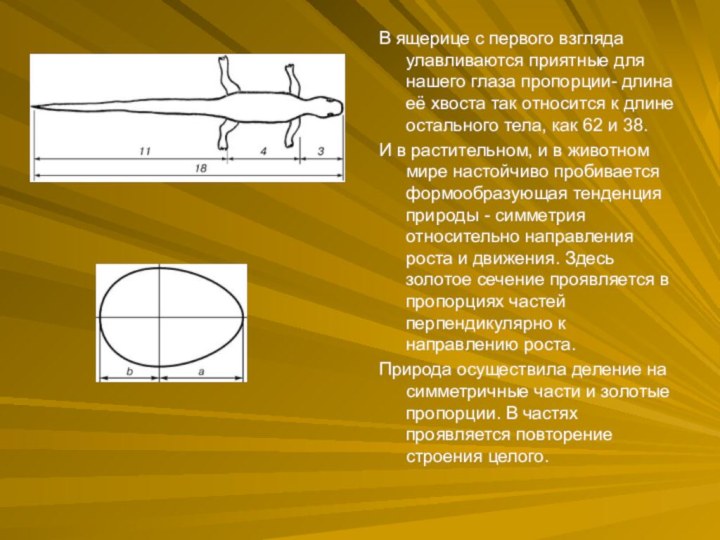
В ящерице с первого взгляда улавливаются приятные для
нашего глаза пропорции- длина её хвоста так относится к
длине остального тела, как 62 и 38.
И в растительном, и в животном мире настойчиво пробивается формообразующая тенденция природы - симметрия относительно направления роста и движения. Здесь золотое сечение проявляется в пропорциях частей перпендикулярно к направлению роста.
Природа осуществила деление на симметричные части и золотые пропорции. В частях проявляется повторение строения целого.
Слайд 19
Практическая часть
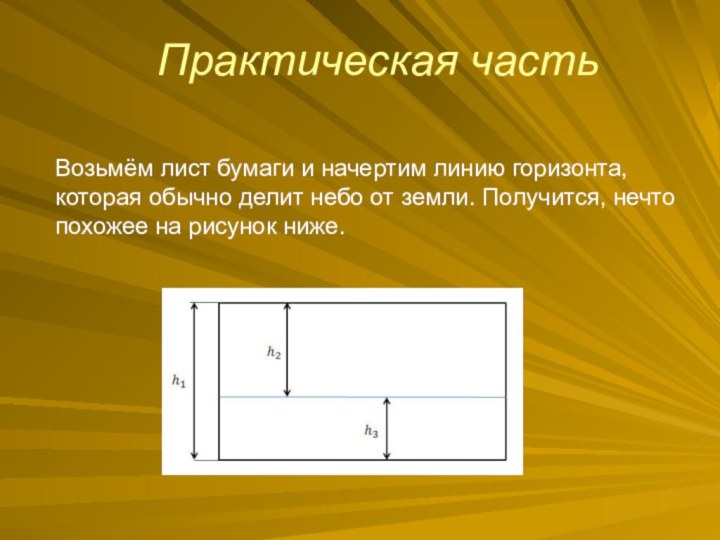
Возьмём лист бумаги и начертим линию горизонта,
которая обычно делит небо от земли. Получится, нечто похожее
на рисунок ниже.
Слайд 20
Отношение высоты картины (h1) к расстоянию от верхнего
края (h2) равно отношению расстояния от верхнего края (h2)
к расстоянию до нижнего края (h3). В виде математической записи, это будет выглядеть так:
Найдём числовое значение золотого сечения.
Для этого вернёмся к нашему рисунку. Пусть высота всей картины равна 1 ( h1 = =1), а расстояние от верхнего края до горизонта обозначим за x (h2 = x). Тогда получим:
1 : x = x : (1 – x)
x2 – x – 1 = 0
Слайд 21
Положительный корень этого уравнения (√5 + 1) /
2 ≈ 1,618… . Это отношение большей части к
меньшей в этой пропорции.
Это число равно отношению золотого сечения. Обычно его обозначают греческими буквами τ (тау) или φ (фи)
Слайд 22
Выводы :
В ходе работы выявлена закономерность образования «Золотого
Сечения»;
Выявлены свойства «Золотой Пропорции»;
Выбранная тема является традиционной для олимпиадных
заданий, поэтому имеет практическое применение.
Слайд 23
Памятник мечте (девочка с мыльными пузырями), автор
скульптуры Дмитрий Иванченко:
1,602=1,663
Слайд 24
Фонтан возле нового здания
БелГУ
1,725=1,667
Слайд 26
Храм на набережной возле нового здания БелГУ
1,605=1,689
Слайд 27
Здание театра имени И. Щепкина
1,604=1,709
Слайд 28
Выводы:
В ходе работы выявлена закономерность образования «Золотого
Сечения»;
Выявлены свойства «Золотой Пропорции»;
Выбранная тема является традиционной для олимпиадных
заданий, поэтому имеет практическое применение.