изучения
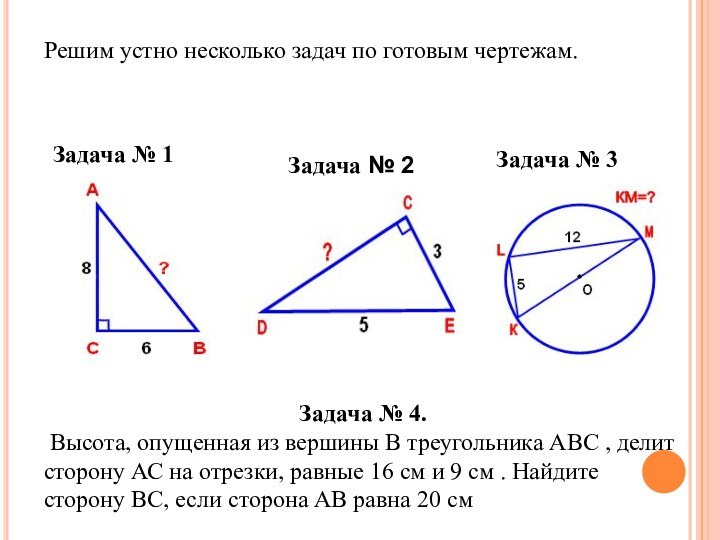
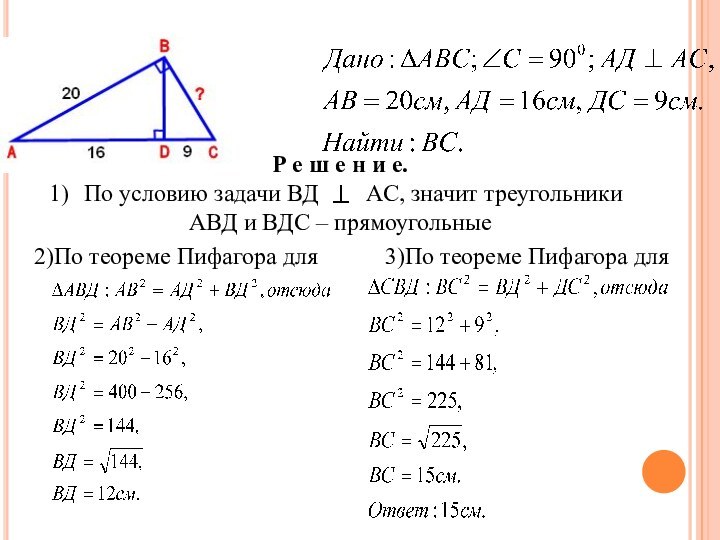
Существенно расширить круг геометрических задач, решаемых школьниками
Познакомить учащихся с
основными этапами жизни и деятельности Пифагора.Осуществление межпредметной связи геометрии с алгеброй, геометрией, историей, биологией, литературой.