- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
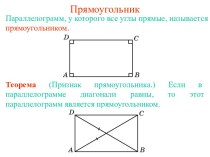
Презентация на тему Компланарные векторы
Содержание
- 2. Цели урокаВвести определение компланарных векторов.Рассмотреть признак компланарности трех векторов и правило параллелепипеда, сложение трех некомпланарных векторов.
- 3. Новый материалОпределение.Векторы называются компланарными, если при откладывании
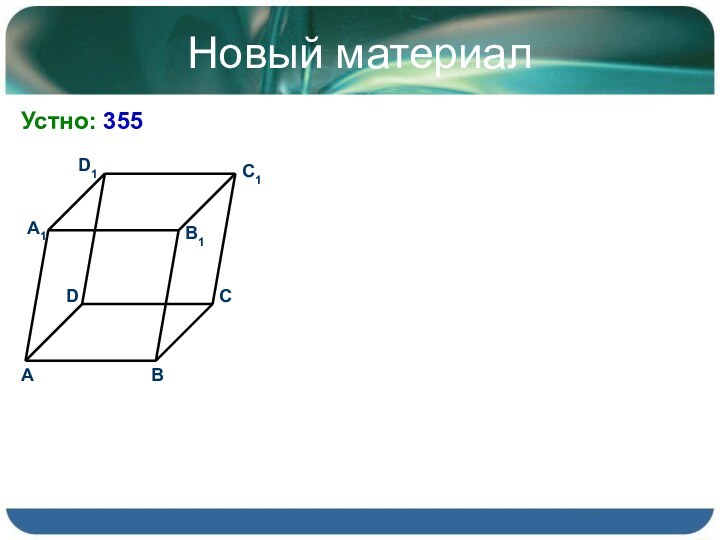
- 4. Новый материалУстно: 355
- 5. Новый материалПризнак компланарности трех векторов:
- 6. Новый материалПризнак компланарности трех векторов:•ОА1В1С
- 7. Новый материал356
- 8. Новый материал356
- 9. Новый материалОпределение.Утверждение, обратное признаку компланарности векторов:Докажем это.
- 10. Новый материалОАВРР1Так как векторы компланарны, то они лежат в одной плоскости.
- 11. Новый материалМы умеем на плоскости складывать векторы
- 12. Решение упражнений360(а)Определение.
- 13. Домашнее заданиеп. 39, 40вопросы 13-15 стр. 97358, 360(б), 368(а, б)
- 14. Скачать презентацию
- 15. Похожие презентации
Цели урокаВвести определение компланарных векторов.Рассмотреть признак компланарности трех векторов и правило параллелепипеда, сложение трех некомпланарных векторов.













Слайд 2
Цели урока
Ввести определение компланарных векторов.
Рассмотреть признак компланарности трех
векторов и правило параллелепипеда, сложение трех некомпланарных векторов.
Слайд 3
Новый материал
Определение.
Векторы называются компланарными, если при откладывании от
одной и той же точки они будут лежать в
одной плоскости.Иначе: векторы называются компланарными, если имеются равные им векторы, лежащие в одной плоскости.
Любые два вектора компланарны.
Три вектора, среди которых имеются два коллинеарных, также компланарны.
Почему?
Три произвольных вектора могут быть как компланарными, так и некомпланарными.
Слайд 9
Новый материал
Определение.
Утверждение, обратное признаку компланарности векторов:
Докажем это.
Слайд 11
Новый материал
Мы умеем на плоскости складывать векторы по
правилу треугольника и параллелограмма. А если в пространстве?
Для сложения
трех некомпланарных векторов пользуются правилом параллелепипеда. В чем оно заключается?Е
С
В
А
О
D
B1
A1