- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему по геометрии Решение задач повышенной сложности в курсе стереометрии.
Содержание
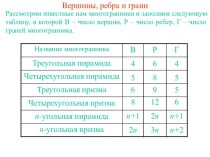
- 2. Таблица самооценки.
- 5. V=1/3Sпс L , Sпс площадь сечения, перпедикулярного ребру L пирамиды
- 9. Дополнительные соотношения между элементами призмы и пирамиды.
- 10. Пусть в пирамиде: все боковые ребра образуют
- 11. Пусть в пирамиде:-все боковые грани образуют с
- 12. Если в наклонной призме боковое ребро составляет
- 13. Если высота треугольной пирамиды проходит через точку
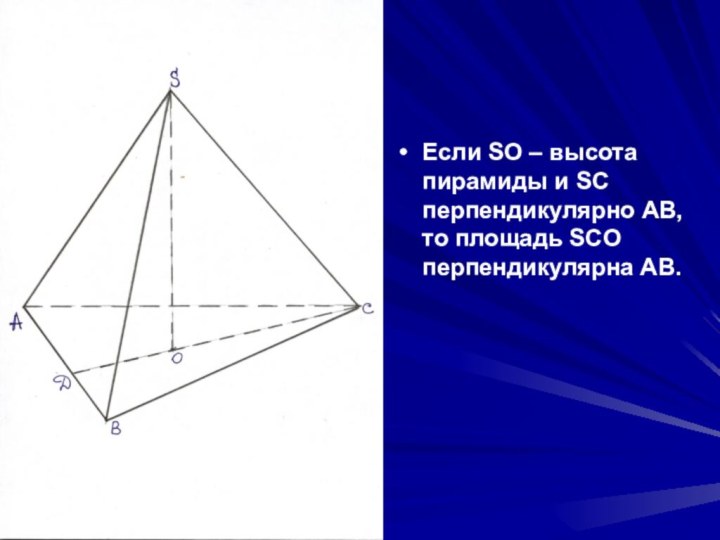
- 14. Если SO – высота пирамиды и SС перпендикулярно АB, то площадь SСO перпендикулярна АВ.
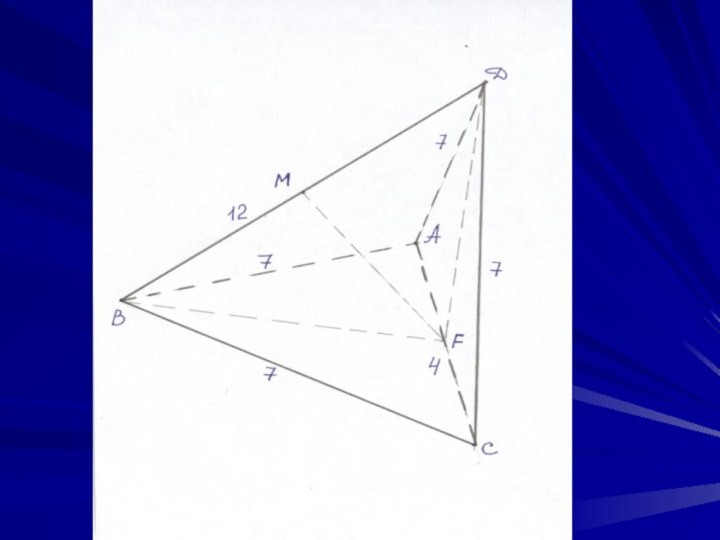
- 15. Решите задачуВычислить объем треугольной пирамиды, у которой
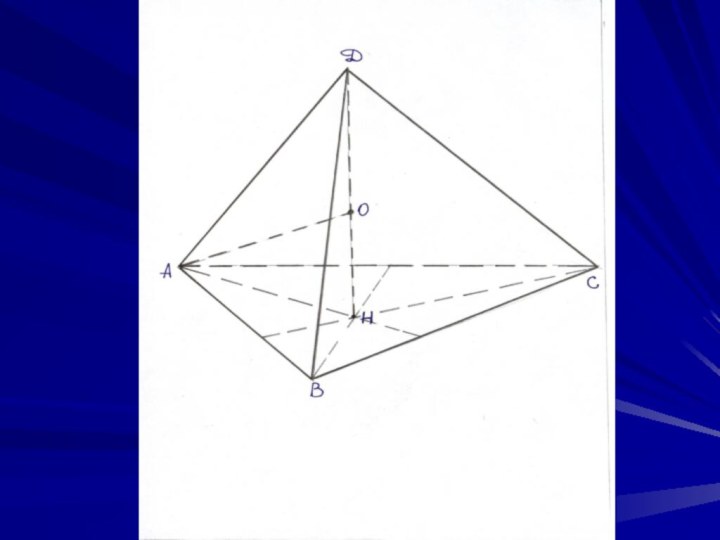
- 17. Ортоцентрический тетраэдр – высоты тетраэдра пересекаются в одной точке.
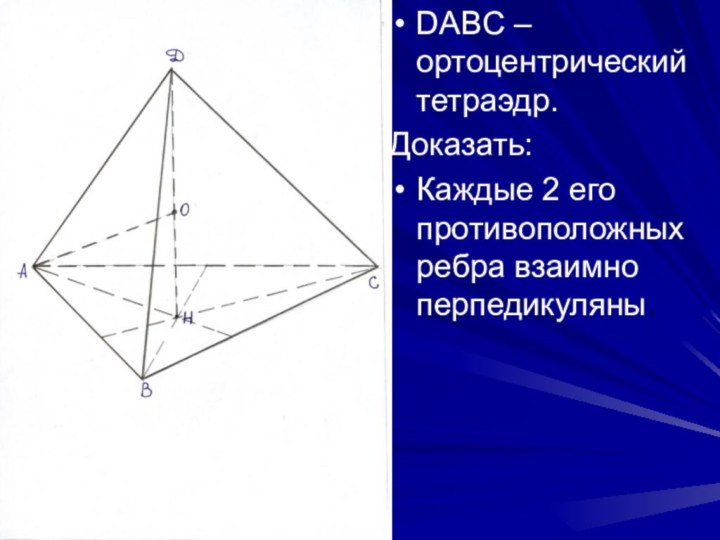
- 19. DABC – ортоцентрический тетраэдр.Доказать: Каждые 2 его противоположных ребра взаимно перпедикуляны.
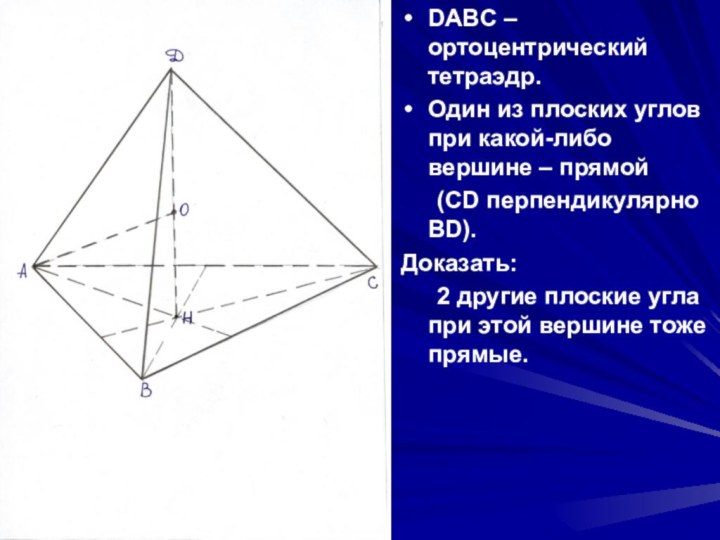
- 20. DABC – ортоцентрический тетраэдр.Один из плоских углов
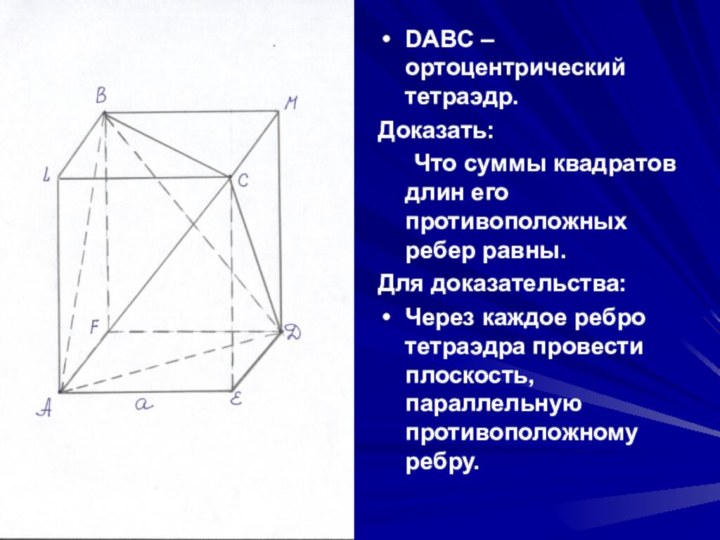
- 21. DABC – ортоцентрический тетраэдр.Доказать: Что суммы квадратов длин
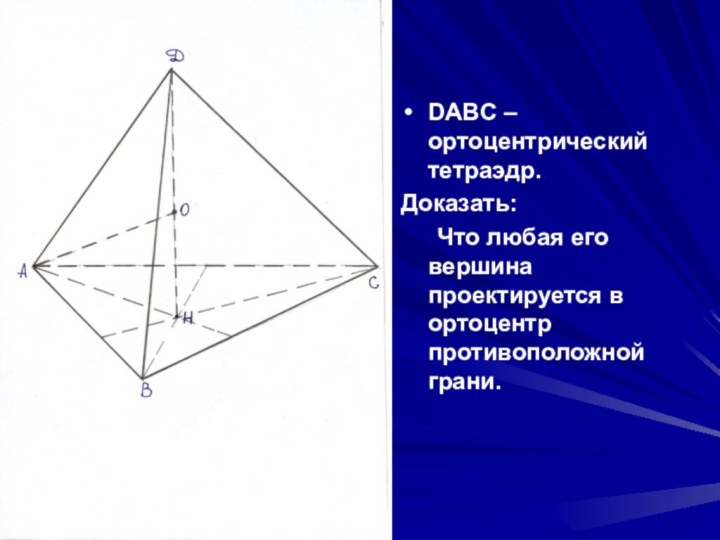
- 22. DABC – ортоцентрический тетраэдр.Доказать: Что любая его вершина проектируется в ортоцентр противоположной грани.
- 23. Скачать презентацию
- 24. Похожие презентации
Таблица самооценки.
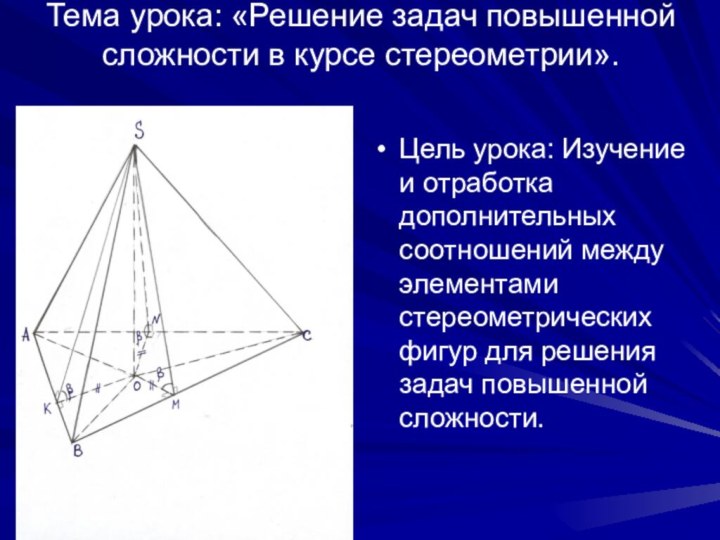












Слайд 10
Пусть в пирамиде:
все боковые ребра образуют с
плоскостью основания равные углы;
или
-длины всех боковых ребер равны.
Вершина пирамиды
проецируется в центр описанной около основания окружности (пересечение срединных перпендикуляров основания).
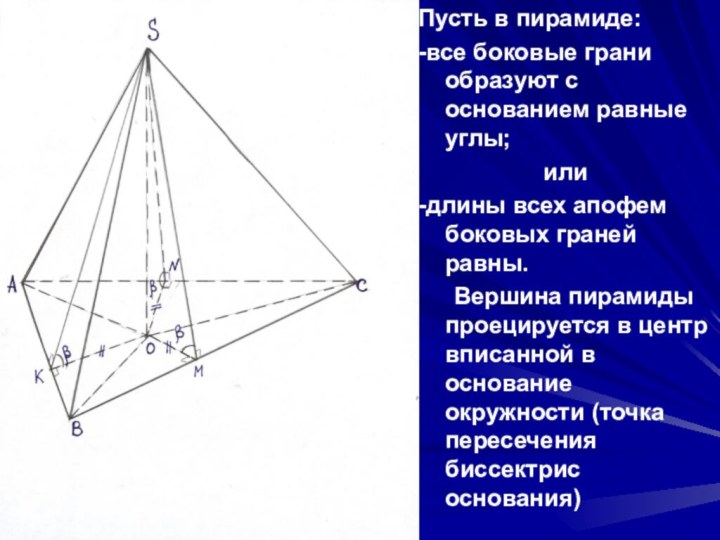
Слайд 11
Пусть в пирамиде:
-все боковые грани образуют с основанием
равные углы;
или
-длины всех апофем боковых граней равны.
Вершина пирамиды проецируется
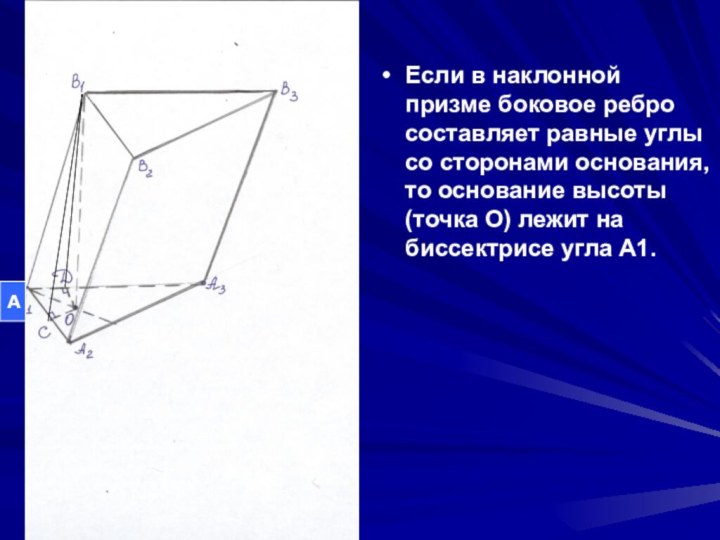
в центр вписанной в основание окружности (точка пересечения биссектрис основания) Слайд 12 Если в наклонной призме боковое ребро составляет равные
углы со сторонами основания, то основание высоты (точка О)
лежит на биссектрисе угла А1.А
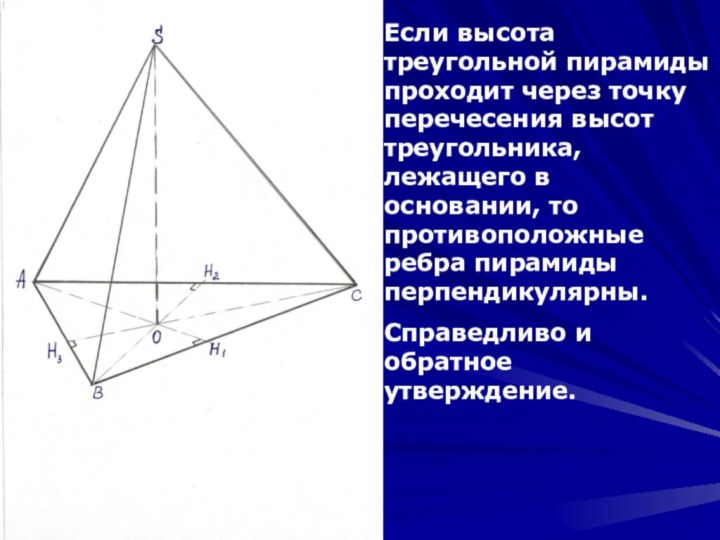
Слайд 13 Если высота треугольной пирамиды проходит через точку перечесения
высот треугольника, лежащего в основании, то противоположные ребра пирамиды
перпендикулярны.Справедливо и обратное утверждение.