две
противоположные стороны можно назвать
основаниями.
Расстояние между ними( по
перпендикуляру)называется высотой.
ABCD
BCAD
BH AD
В
- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Площади четырехугольников
Содержание
- 2. ПараллелограммАВСDПараллелограмм есть четырехугольник, противоположные стороны которогопопарно параллельны.
- 3. Признаки параллелограмма Четырехугольник является параллелограммом, если выполняется
- 4. ТрапецияТрапецией называется четырехугольник, у которого две стороны
- 5. ПрямоугольникПрямоугольником называется параллелограмм,у которого все углы прямые.
- 6. Ромб и квадрат АВСDРомб-это параллелограмм, у которого
- 7. Площади четырехугольниковПроизвольный четырехугольник(аd1d2Основные свойства площадей1. Равные многоугольники
- 8. Площадь прямоугольника, параллелограмма и квадрата.АB
- 9. Скачать презентацию
- 10. Похожие презентации
ПараллелограммАВСDПараллелограмм есть четырехугольник, противоположные стороны которогопопарно параллельны. Любые двепротивоположные стороны можно назвать основаниями. Расстояние между ними( по перпендикуляру)называется высотой.ABCDBCADBH ADВ
Слайд 2
Параллелограмм
А
В
С
D
Параллелограмм есть четырехугольник,
противоположные стороны которого
попарно параллельны. Любые
две
перпендикуляру)называется высотой.
Слайд 3
Признаки параллелограмма
Четырехугольник является параллелограммом, если выполняется одно из
следующих
условий:
Противоположные стороны попарно равны
2) Две противоположные стороны равны и
параллельны3)Диагонали параллелограмма точкой пересечения делятся пополам.
Слайд 4
Трапеция
Трапецией называется четырехугольник, у которого две стороны параллельны,
а две другие стороны не параллельны.
В
А
С
D
Параллельные стороны трапеции называются
ее
основаниями, а две другие стороны-боковыми сторонами. Трапеция называется
равнобедренной, если ее боковые стороны
равны. Трапеция, один из углов которой прямой,
называется прямоугольной.
А
В
С
D
Прямоугольная трапеция
С
=90
Слайд 5
Прямоугольник
Прямоугольником называется параллелограмм,
у которого все углы прямые. Так
как прямоугольник
является параллелограммом, то он обладает всеми
свойствами параллелограмма:
в прямоугольникепротивоположные стороны равны, а диагонали
точкой пересечения делятся пополам.
Рассмотрим особое свойство прямоугольника.
Диагонали прямоугольника равны.
А
В
С
D
В прямоугольнике квадрат диагонали равен
сумме квадратов двух смежных сторон.
Слайд 6
Ромб и квадрат
А
В
С
D
Ромб-это параллелограмм, у которого
все стороны
равны.
Свойства ромба:
1)Диагонали ромба пересекаются под прямым углом.
2)Диагонали ромба
являются биссектрисами его углов.А
В
С
D
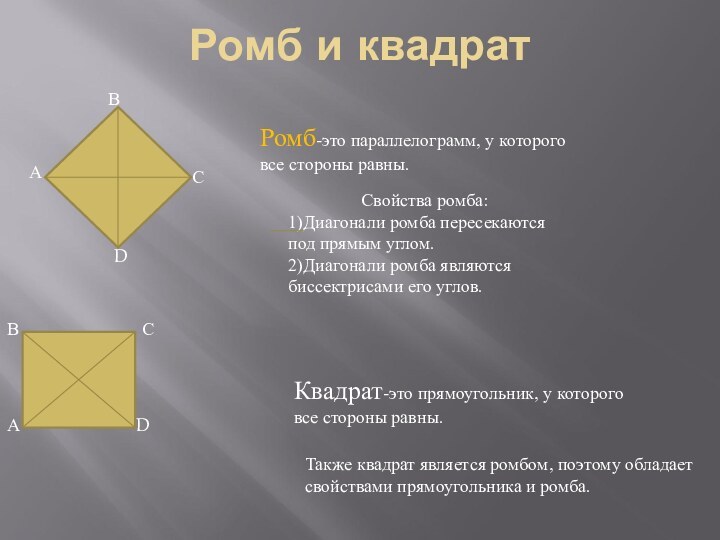
Квадрат-это прямоугольник, у которого
все стороны равны.
Также квадрат является ромбом, поэтому обладает
свойствами прямоугольника и ромба.
Слайд 7
Площади четырехугольников
Произвольный четырехугольник
(
а
d1
d2
Основные свойства площадей
1. Равные многоугольники имеют
равные площади.
2. Если многоугольник составлен из нескольких многоугольников, то
его площадь равна сумме площадей этих многоугольников.F1
F2
F3
F4
SABCD= SF1+SF2+SF3+SF4
A
B
C
D
Площадь любого произвольного четырехугольника
