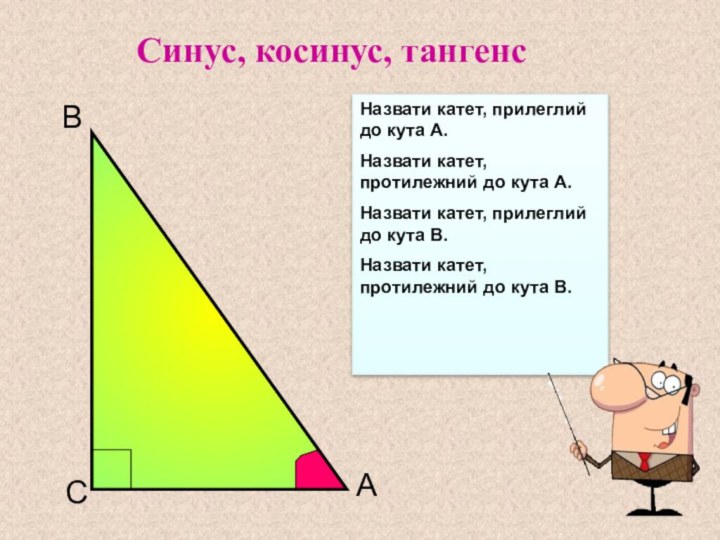
до кута А.
Назвати катет, прилеглий до кута В.
Назвати катет,
протилежний до кута В.Синус, косинус, тангенс
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Email: Нажмите что бы посмотреть

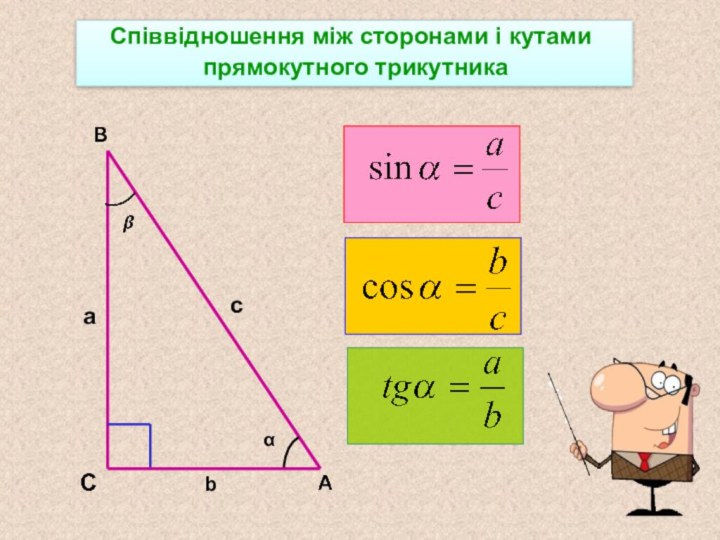
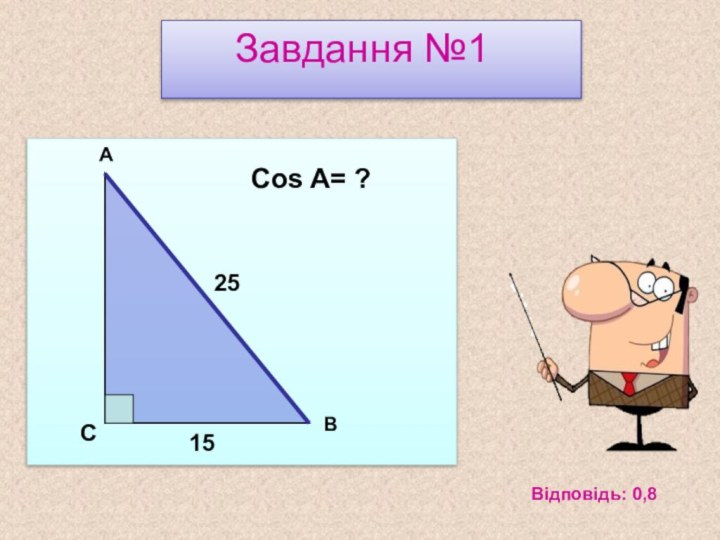
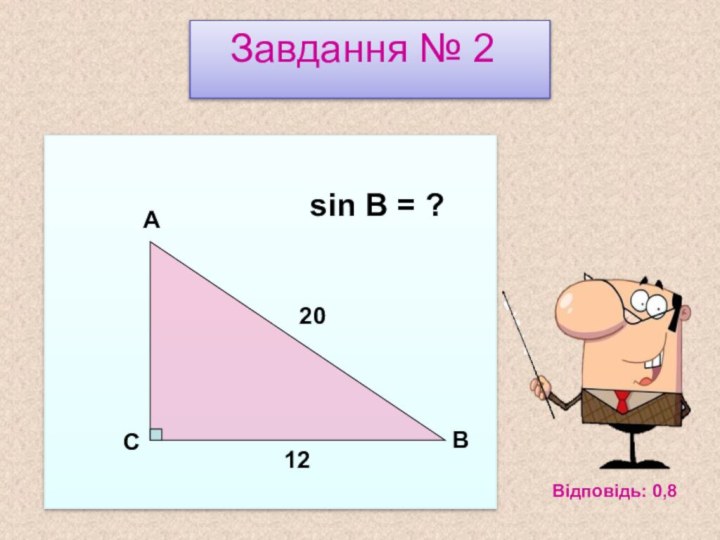



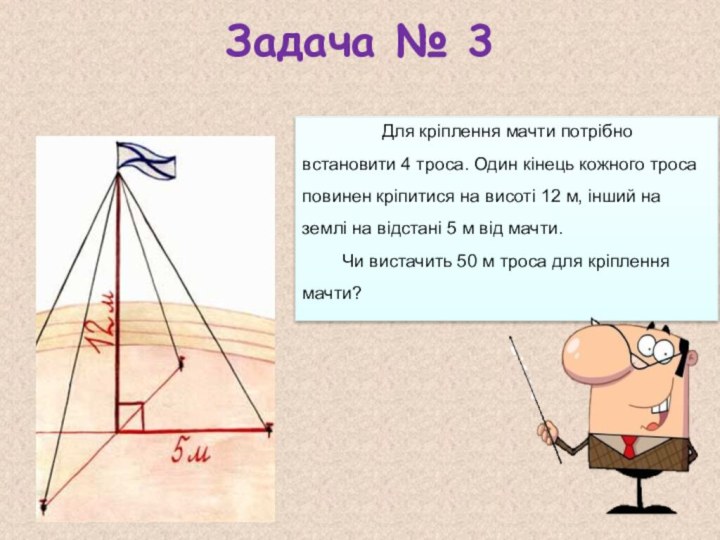


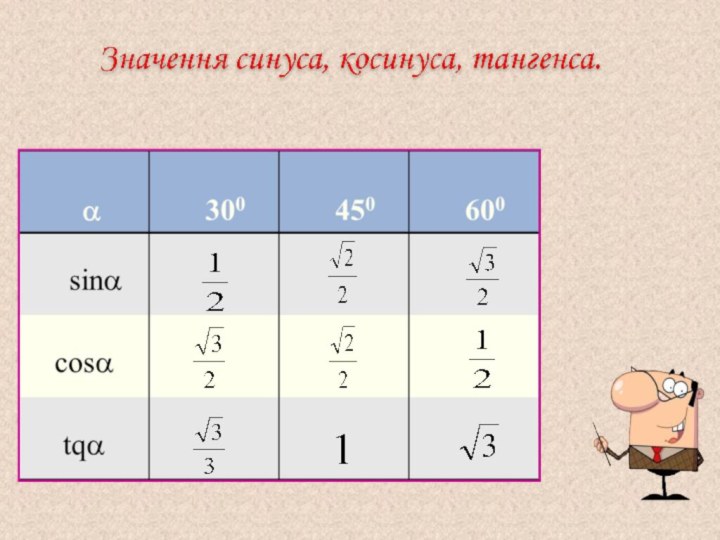
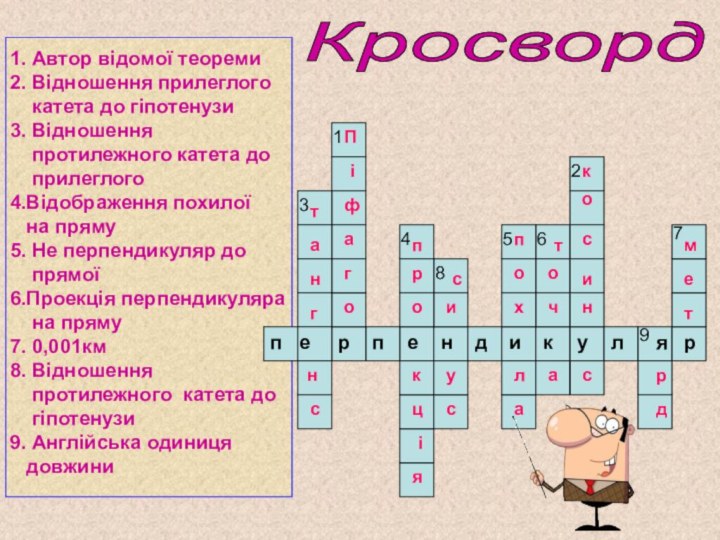


Синус, косинус, тангенс
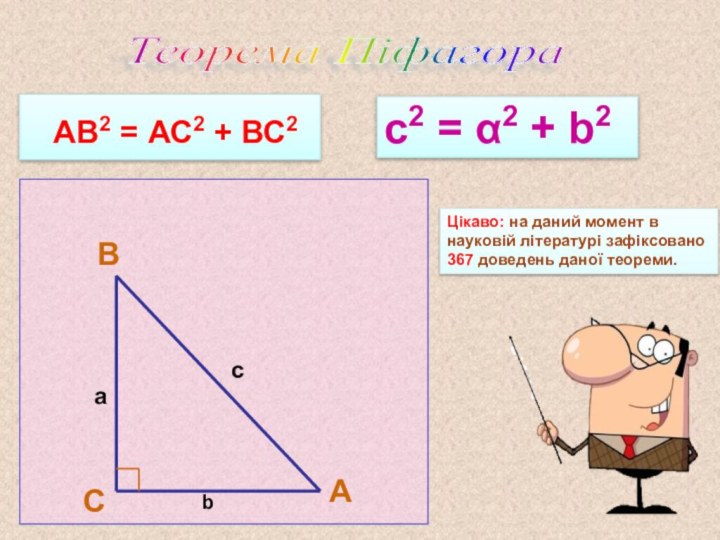
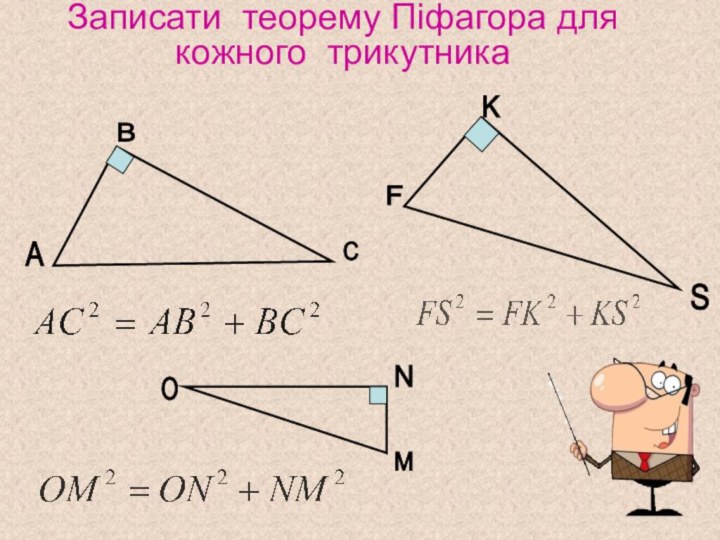
Теорема Піфагора
За теоремою Піфагора : ВС² + АС² = АВ², тому
Доведення:
п
е
р
п
е
н
д
и
к
у
л
я
р
П
і
ф
а
г
о
к
о
с
и
н
с
т
а
н
г
н
с
п
р
о
к
ц
і
я
п
о
х
л
а
т
о
ч
а
м
е
т
с
и
у
с
р
д