- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему по геометрии 9 класса на тему Построение правильных многоугольников
Содержание
- 2. Выпуклый многоугольник называется правильным, если у него все углы равны и все стороны равны
- 3. Правильный многоугольник является вписанным в окружность и описанным около окружности, причем центры этих окружностей совпадают.
- 4. Около любого правильного многоугольника можно описать окружность
- 5. Простейшее построение правильного четырехугольникаПостроение правильного восьмиуголь- ника
- 7. Решение. Пусть w- данная окружность радиуса R
- 8. Построение правильных многоугольников, то есть деление окружности
- 9. Именно в школе ПИФАГОРА зародилось учение о
- 10. По некоторым источникам, он являлся автором сочинения
- 11. Описал построение правильных 3 , 4 , 5 , 6- угольников, построил правильный 15-угольник
- 12. Развитие готического стиля и широкое применение витражей
- 13. Именно Альбрехт Дюрер осуществил новое построение
- 14. Дюрер занимался фортификацией, разрабатывая системы оборонительных сооружений;Решил задачу построения правильного восьмиугольника;Разработал принципы черчения художественно исполненных букв.
- 15. Для своего друга Луки Пачоли Леонардо, глубоко
- 16. математик Иоганн Кеплер создал трактат «Новогодний подарок
- 17. Великий математик, механик и инженер древности Архимед
- 18. Доказал возможность построения правильного 17-угольника. После этого 19-летний юноша решил заняться математикой, а не филологией.
- 19. И всё же существует единый способ построения
- 20. А так ли уж важно изучать и
- 21. Платоновы телаПлатоновы тела - трехмерный аналог плоских
- 23. Скачать презентацию
- 24. Похожие презентации
Выпуклый многоугольник называется правильным, если у него все углы равны и все стороны равны





















Слайд 2 Выпуклый многоугольник называется правильным, если у него все
углы равны и все стороны равны
Слайд 3 Правильный многоугольник является вписанным в окружность и описанным
около окружности, причем центры этих окружностей совпадают.
Слайд 4
Около любого правильного многоугольника можно описать окружность и
притом только одну.
Центр – точка пересечения биссектрис.
·
О
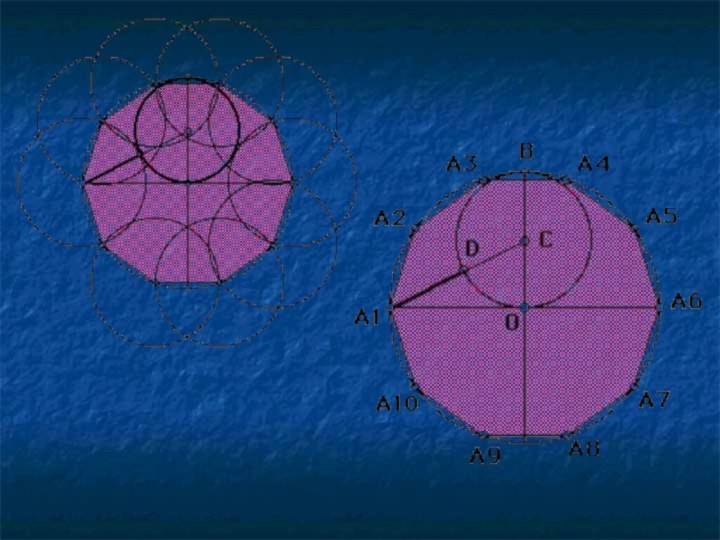
Слайд 7 Решение. Пусть w- данная окружность радиуса R с
центром O и АВ - сторона правильного вписанного в
эту окружность десятиугольника, а АС- сторона правильного вписанного шестиугольника, причем точки В и С расположены на окружности так, как показано на рисунке а). Тогда, очевидно, дуга АВ=36°, дуга АС=60° , поэтому дуга ВС=24° . Следовательно, угол ВОС=24°=360°/15°, и, значит, отрезок ВС- сторона правильного пятнадцатиугольника, вписанного в окружность w. Так как мы умеем строить циркулем и линейкой отрезки АВ=((корень из 5-1)/2)*R и АС=R (рис.б)), то можем построить отрезок ВС.Возьмем далее на окружности w произвольную точку А1 и, пользуясь циркулем, отметим на этой окружности последовательно точки А2, А3,…, А15 так, что А1А2 = А2А3=…= А14А15= ВС. Проведя затем отрезки А1А2, А2А3,…, А14А15, А15А1, получим искомый правильный пятнадцатиугольник А1А2…А15 (рис. в)).
Слайд 8 Построение правильных многоугольников, то есть деление окружности на
равные части, позволяло решать практические задачи:
1)Создание колеса со спицами;
2)Деление
циферблата часов;3)Строительство античных театров;
4)Создание астрономических сооружений
Слайд 9 Именно в школе ПИФАГОРА зародилось учение о правильных
многоугольниках; кроме того, пифагорейцы рассмотрели вопрос покрытия плоскости правильными
многоугольниками.Слайд 10 По некоторым источникам, он являлся автором сочинения о
правильных многоугольниках, часто присоединяемого к "Началам" в качестве XV
книги. Исидор из Милета (532-537 гг.) - византийский архитектор и геометр, построивший вместе с Анфи - мием собор Святой Софии в Константинополе.Слайд 12 Развитие готического стиля и широкое применение витражей в
строительстве соборов также заставило вернуться к задачам построения правильных
многоугольников.Слайд 13 Именно Альбрехт Дюрер осуществил новое построение правильного
пятиугольника, передав потомкам средневековый способ построения постоянным раствором циркуля.
Слайд 14
Дюрер занимался фортификацией, разрабатывая системы оборонительных сооружений;
Решил задачу
построения правильного восьмиугольника;
Разработал принципы черчения художественно исполненных букв.
Слайд 15 Для своего друга Луки Пачоли Леонардо, глубоко интересующийся
пропорциями, создал иллюстрации многогранников, гранями которых являются правильные многоугольники.
Слайд 16 математик Иоганн Кеплер создал трактат «Новогодний подарок или
о шестиугольных снежинках», опубликованный в 1611 году. В нем
он практически привел первый пример разбиения плоскости на правильные шестиугольники.Слайд 17 Великий математик, механик и инженер древности Архимед (греч.(греч.
Αρχιμήδης, родился 287 до н. э.(греч. Αρχιμήδης, родился 287
до н. э. - 212 до н. э.)Периметр (сумма длин сторон) правильного n-угольника при заданном числе сторон n наиболее близок к длине его описанной окружности среди всех вписанных в нее n-угольников; таким же свойством он обладает и по отношению к вписанной окружности. Поскольку вычисление длины окружности считалось в древности весьма важной задачей, много усилий было затрачено на то, чтобы научиться оценивать периметр вписанной в нее правильного многоугольника при достаточно больших n. Особенно преуспел в этом Архимед.
Слайд 18 Доказал возможность построения правильного 17-угольника. После этого 19-летний
юноша решил заняться математикой, а не филологией.
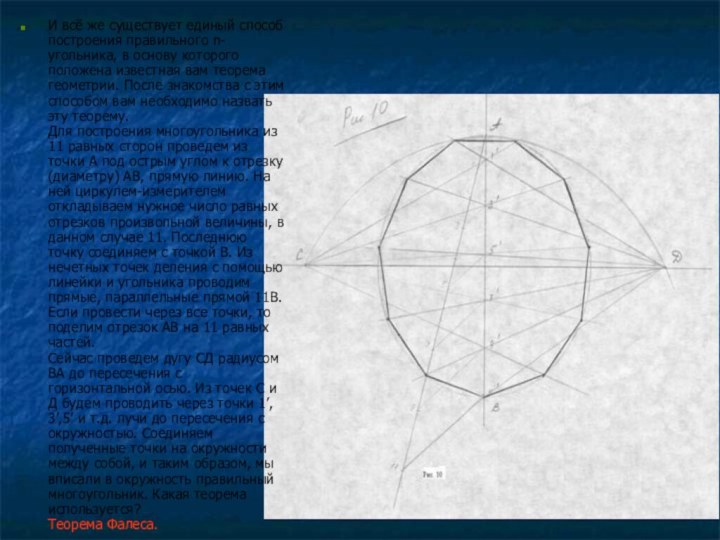
Слайд 19 И всё же существует единый способ построения правильного
n-угольника, в основу которого положена известная вам теорема геометрии.
После знакомства с этим способом вам необходимо назвать эту теорему. Для построения многоугольника из 11 равных сторон проведем из точки А под острым углом к отрезку (диаметру) АВ, прямую линию. На ней циркулем-измерителем откладываем нужное число равных отрезков произвольной величины, в данном случае 11. Последнюю точку соединяем с точкой В. Из нечетных точек деления с помощью линейки и угольника проводим прямые, параллельные прямой 11В. Если провести через все точки, то поделим отрезок АВ на 11 равных частей. Сейчас проведем дугу СД радиусом ВА до пересечения с горизонтальной осью. Из точек С и Д будем проводить через точки 1’, 3’,5’ и т.д. лучи до пересечения с окружностью. Соединяем полученные точки на окружности между собой, и таким образом, мы вписали в окружность правильный многоугольник. Какая теорема используется? Теорема Фалеса.Слайд 20 А так ли уж важно изучать и знать
сведения о правильных многоугольниках? В каких житейских ситуациях можно
встретиться с правильными многоугольниками?Историческая справка.
В математике паркетом называют «замощение» плоскости повторяющимися фигурами без пропусков и перекрытий. Простейшие паркеты были открыты пифагорейцами около 2500 лет тому назад. Они установили, что вокруг одной точки могут лежать либо шесть правильных многоугольников (3600: 600 = 6), либо четыре квадрата (3600: 900 = 4), либо три правильных шестиугольника (3600: 1200 = 3), так как сумма углов с вершиной этой точки равна 3600. Вы не задумывались вот над таким вопросом: Почему пчелы «выбрали» себе для ячеек на сотах форму правильного шестиугольника?
Пчелы – удивительные творения природы. Свои геометрические способности они проявляют при построении своих сот. Если возьмем равносторонний треугольник, квадрат и правильный шестиугольник одинаковой площади (показываю модели), то периметр шестиугольника будет наименьшим. (Р3 = 45,9 см., Р4 = 40 см., Р6 = 37,8 см.).
Строя шестиугольные ячейки пчелы наиболее экономно используют площадь внутри небольшого улья и воск для изготовления ячеек.
Причем пчелиные соты представляют собой не плоский, а пространственный паркет, поскольку заполняют пространство так, что не остается просветов.
И как не согласиться с мнением пчелы из сказки «Тысяча и одна ночь»: «Мой дом построен по законам самой строгой архитектуры. Сам Евклид мог бы поучиться, познавая геометрию моих сот».
Слайд 21
Платоновы тела
Платоновы тела - трехмерный аналог плоских правильных
многоугольников.
Существует лишь пять выпуклых правильных многогранников - тетраэдр, октаэдр
и икосаэдр с треугольными гранями, куб (гексаэдр) с квадратными гранями и додекаэдр с пятиугольными гранями. Доказательство этого факта известно уже более двух тысяч лет; этим доказательством и изучением пяти правильных тел завершаются "Начала" Евклида.Существование только пяти правильных многогранников относили к строению материи и Вселенной. Пифагорейцы, а затем Платон полагали, что материя состоит из четырех основных элементов: огня, земли, воздуха и воды
.Согласно их мнению, атомы основных элементов должны иметь форму различных Платоновых тел.