- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему по геометрии по теме Параллельность плоскостей
Содержание
- 2. Параллельные плоскости в пространствеОпределение. Две плоскости в пространстве называются параллельными, еслиони не пересекаются.
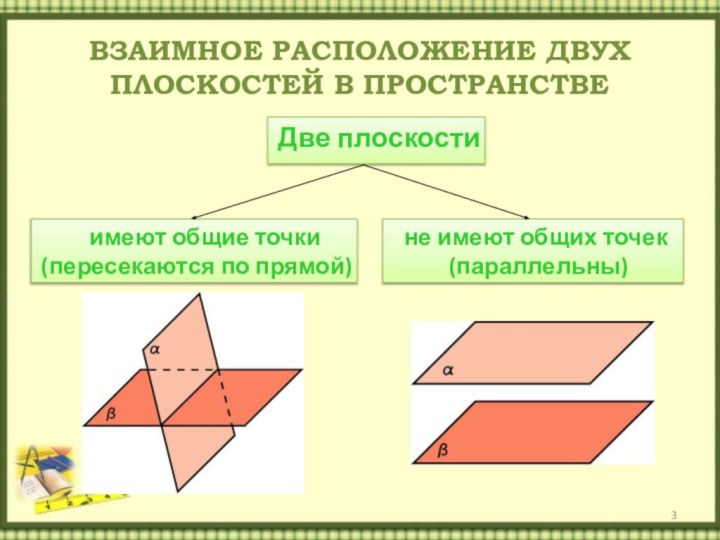
- 3. ВЗАИМНОЕ РАСПОЛОЖЕНИЕ ДВУХ ПЛОСКОСТЕЙ В ПРОСТРАНСТВЕ
- 4. Признак параллельности плоскостей Теорема. Если две пересекающиеся прямые
- 5. Задача № 51. (еще один признак параллельности)Дано:
- 6. http://aida.ucoz.ruСвойства параллельных плоскостей
- 7. Если две параллельные плоскости пересечены третьей,
- 8. Отрезки параллельных прямых,
- 9. Решение задачЯвляются ли параллельными плоскости ABC и B1C1D1, проходящие через вершины куба A…D1? Ответ: Да.
- 10. Задача . Дано: отрезки А1А2, В1В2, С1С2
- 11. Скачать презентацию
- 12. Похожие презентации



Слайд 2
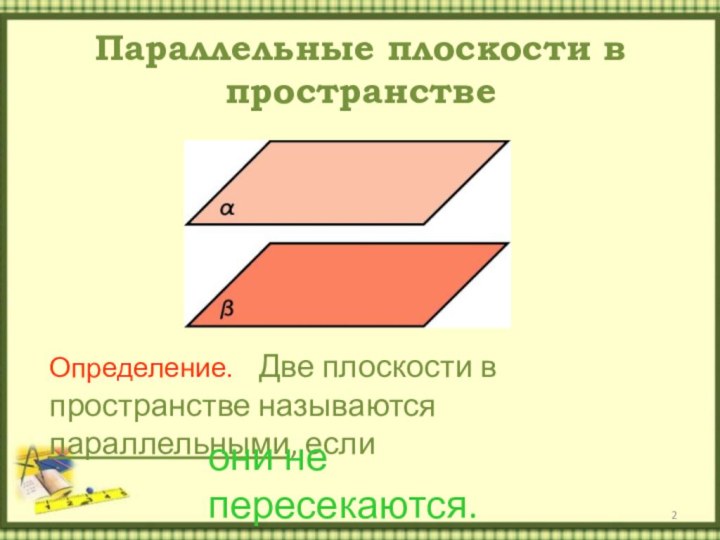
Параллельные плоскости в пространстве
Определение. Две плоскости в
пространстве называются параллельными, если
Слайд 4
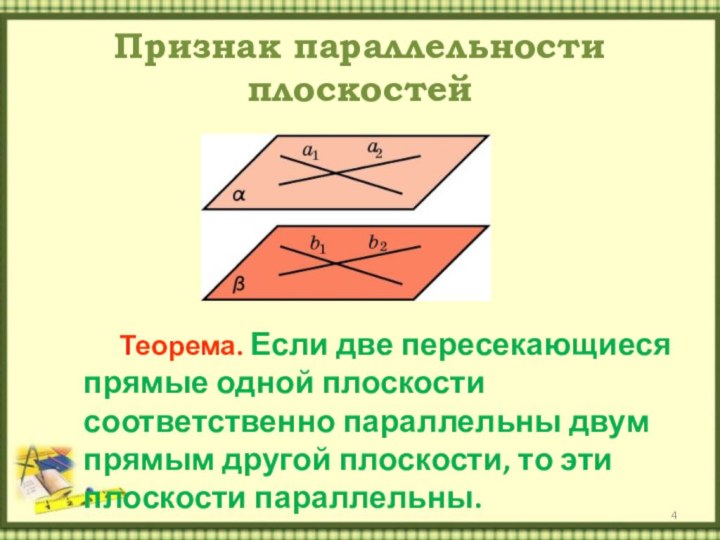
Признак параллельности плоскостей
Теорема. Если две пересекающиеся прямые одной
плоскости соответственно параллельны двум прямым другой плоскости, то эти
плоскости параллельны.
Слайд 5
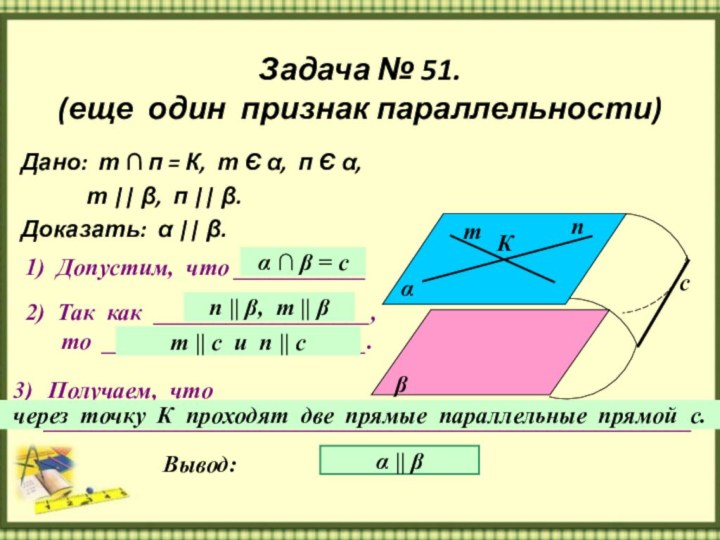
Задача № 51.
(еще один признак параллельности)
Дано: т ∩
п = К, т Є α, п Є α,
т || β, п || β.Доказать: α || β.
1) Допустим, что ___________
2) Так как __________________,
то ______________________.
Получаем, что
______________________________________________________.
Вывод:
α ∩ β = с
п || β, т || β
т || с и п || с
через точку К проходят две прямые параллельные прямой с.
α || β
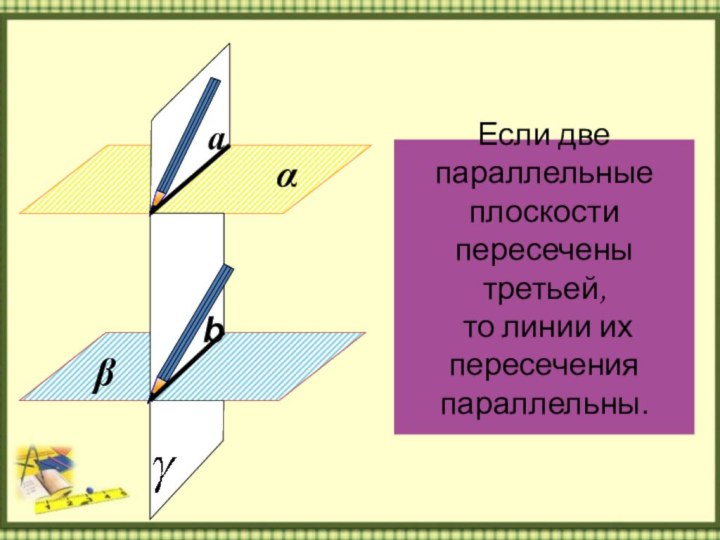
Слайд 7 Если две параллельные плоскости пересечены третьей, то
линии их пересечения
параллельны.α
β
а
b
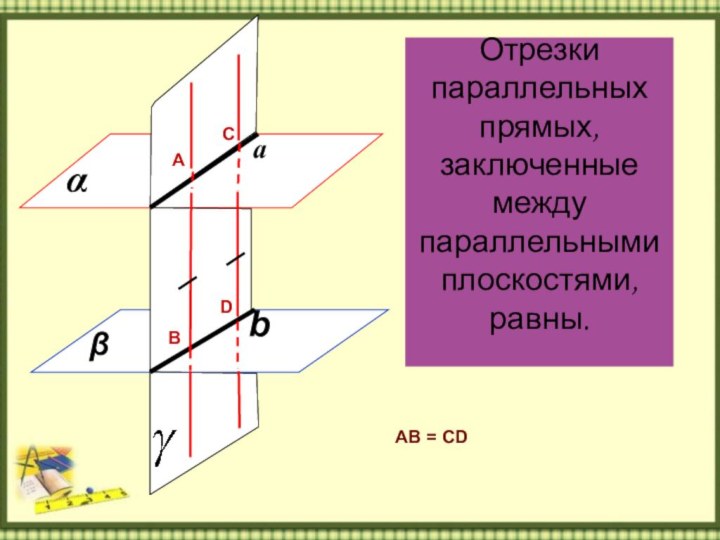
Слайд 8 Отрезки параллельных прямых,
заключенные
между параллельными плоскостями, равны.α
β
а
b
АВ = СD
Слайд 9
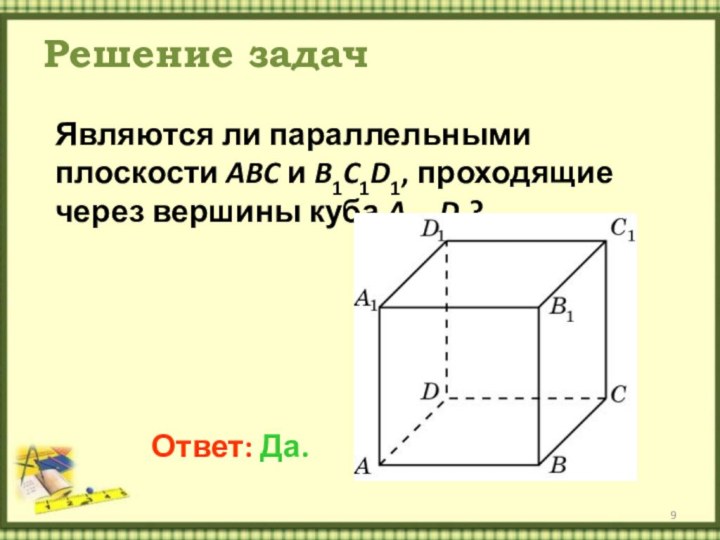
Решение задач
Являются ли параллельными плоскости ABC и B1C1D1,
проходящие через вершины куба A…D1?
Ответ: Да.
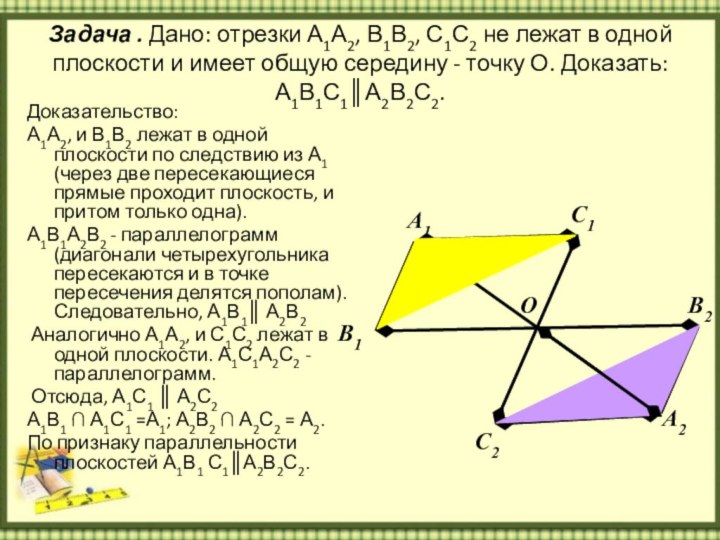
Слайд 10 Задача . Дано: отрезки А1А2, В1В2, С1С2 не
лежат в одной плоскости и имеет общую середину -
точку О. Доказать: А1В1С1║А2В2С2.Доказательство:
А1А2, и В1В2 лежат в одной плоскости по следствию из А1 (через две пересекающиеся прямые проходит плоскость, и притом только одна).
А1В1А2В2 - параллелограмм (диагонали четырехугольника пересекаются и в точке пересечения делятся пополам). Следовательно, А1В1║ А2В2
Аналогично А1А2, и С1С2 лежат в одной плоскости. А1С1А2С2 - параллелограмм.
Отсюда, А1С1 ║ А2С2
А1В1 ∩ А1С1 =А1; А2В2 ∩ А2С2 = А2.
По признаку параллельности плоскостей А1В1 С1║А2В2С2.
А1
В1
А2
В2
С2
С1
О