Презентация на тему Многогранники

называются диагоналями.
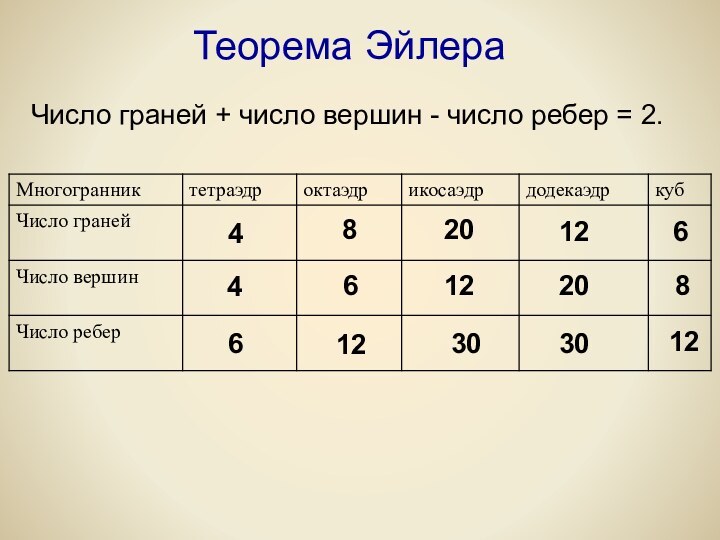
Многогранником
называется тело,
поверхность которого
состоит из конечного

Стороны и вершины этих многоугольников
называются ребрами и вершинами.

которого
состоит из шести параллелограммов
Параллелепипед называется прямоугольным, если все

Куб

Прямоугольный параллелепипед

Параллелепипед

многоугольников и параллелограммов, имеющих общие стороны с каждым из

вы
с
ота

п
р
я
м
а
я

н
а
к
л
о
н
н
а
я

Призма

Два равных многоугольника называют основаниями призмы

Параллелограммы называют
боковыми гранями призмы

Перпендикуляр, проведенный из вершины одного
основания к плоскости другого основания называют
высотой.

поверхности прямой
призмы равна произведению периметра основания
на высоту.
Sбок.

Sполн. =

имеющих общую вершину
Многоугольник называют основанием пирамиды
Треугольники называют боковыми гранями
Общую

Перпендикуляр РН называют высотой

Sбок. + Sосн.

Н

Р

Пирамида

Sполн. =

РЕ называют апофемой
Теорема: Площадь боковой поверхности правильной
пирамиды

Р

Е

Правильная пирамида

Боковые ребра равны

Боковые грани – равные равнобедренные треугольники

Основание высоты совпадает
с центром вписанной или
описанной окружности

правильной
усеченной пирамиды равна половине произведения
полусуммы периметров оснований