- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему по геометрии на тему: Параллельные прямые (7 класс).
Содержание
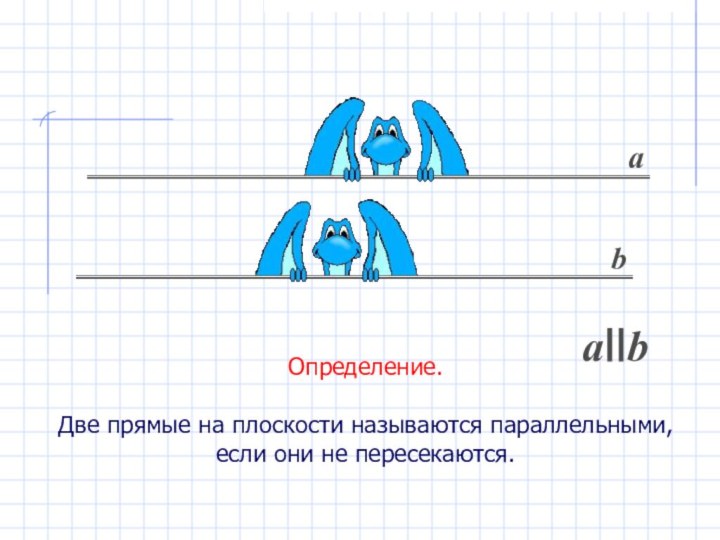
- 2. Определение.Две прямые на плоскости называются параллельными, если они не пересекаются.аbаIIb
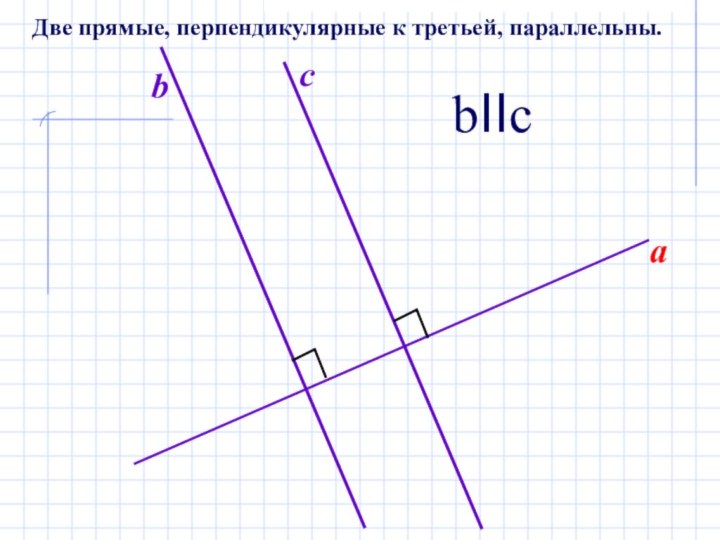
- 3. abcbIIcДве прямые, перпендикулярные к третьей, параллельны.
- 4. 1. Если при пересечении двух прямых
- 6. 64О3Углы 5 и 6 равны, значит, угол
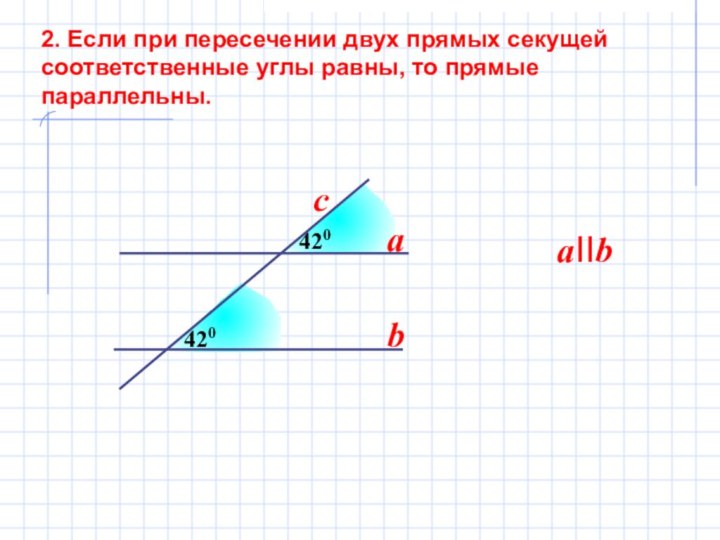
- 7. 420 2. Если при пересечении двух
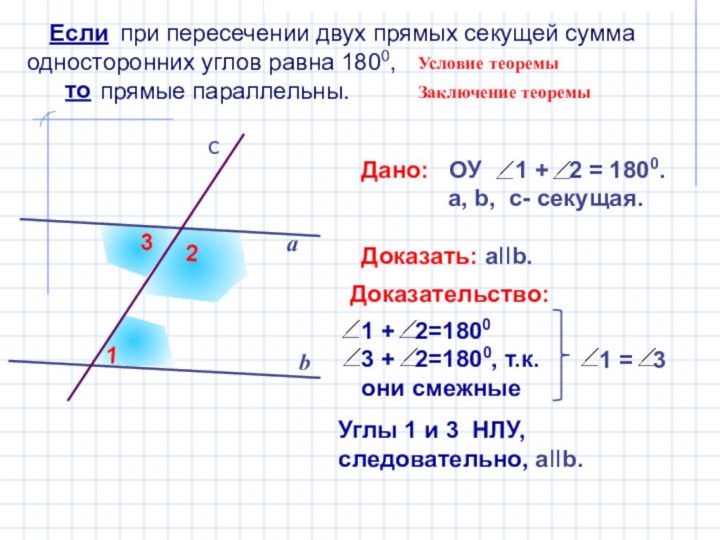
- 9. 3. Если при пересечении двух
- 10. Скачать презентацию
- 11. Похожие презентации

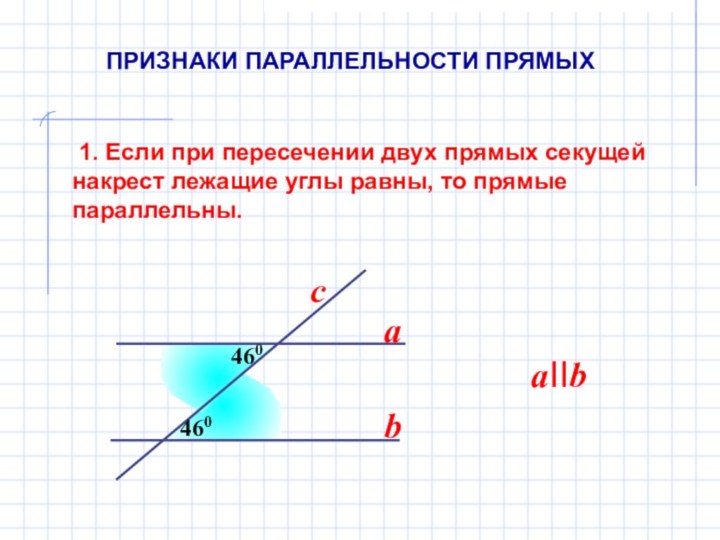




Слайд 4 1. Если при пересечении двух прямых секущей
накрест лежащие углы равны, то прямые параллельны.
460
460
a
b
aIIb
c
ПРИЗНАКИ ПАРАЛЛЕЛЬНОСТИ ПРЯМЫХ
Слайд 5 при
пересечении двух прямых секущей накрест
лежащие углы равны,
прямые параллельны.
b
а
Дано: НЛУ 1 = 2.
а, b, c- секущая.
Доказать: aIIb.
Доказательство: 1 случай
Если углы 1 и 2 прямые,
то прямые а и b перпендикулярны
к прямой АВ, следовательно, aIIb.
Если
то
Условие теоремы
Заключение теоремы
А
1
2
В
c
Слайд 6
6
4
О
3
Углы 5 и 6 равны,
значит, угол 6
– прямой . Значит, прямые a и b перпендикулярны
к прямой НН1, поэтому они параллельны!5
1
2
b
а
c
2 случай
ДП
т.О – середина АВ
ОН a
BH1=AH
АОН= ВОН1 (1 признак)
А
В
Углы 3 и 4 равны,
значит, т.Н1 лежит на продолжении луча ОН, т.е. точки О, Н и Н1 лежат на одной прямой!
Н1
Н
Слайд 7
420
2. Если при пересечении двух прямых
секущей
соответственные углы равны, то прямые
параллельны.420
a
b
aIIb
c
Слайд 8
при
пересечении двух прямых секущей соответственные углы равны,
прямые параллельны.
b
а
Дано: СУ 1 = 2.
а, b, c- секущая.
Доказать: aIIb.
Если
то
Условие теоремы
Заключение теоремы
1
2
c
Углы 1 и 3 НЛУ, следовательно, aIIb.
Доказательство:
Слайд 9 3. Если при пересечении двух прямых
секущей сумма
односторонних углов равна 1800, то прямые
параллельны.
420
1380
a
b
aIIb
c