- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Подобие правильных многоугольников
Содержание
- 2. Цели: доказать теорему о подобии правильных выпуклых
- 3. Актуализация опорных знаний · Какое преобразование фигуры
- 4. Изучение нового материалаТЕОРЕМА. Правильные выпуклые n-угольники подобны
- 5. Доказательство:Докажем второе утверждение.Две фигуры
- 6. Решение задач Выполнить № 32 стр.181.Задача 1.
- 7. Скачать презентацию
- 8. Похожие презентации
Цели: доказать теорему о подобии правильных выпуклых n-угольников, свойство о том, что отношение периметров правильных n-угольников равно отношению радиусов вписанных (описанных) окружностей.







Слайд 3
Актуализация опорных знаний
· Какое преобразование фигуры называется движением?
·
Какими свойствами обладает движение?
· Что такое преобразования подобия?
· Что
такое гомотетия?· Какие фигуры называются равными?
· Какие фигуры называются подобными?
Слайд 4
Изучение нового материала
ТЕОРЕМА. Правильные выпуклые n-угольники подобны (I
ч). В частности, если у них стороны одинаковы, то
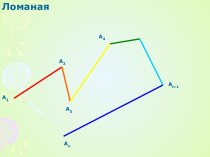
они равны (II ч).Дано:
Р1: А1А2А3…Аn
Р2: В1В2В3…Вn – правильные n-угольники.
А1А2 = В1В2 = …
Доказать:
(I ч) что Р1 Р2
(II ч) Р1 = Р2
Слайд 5
Доказательство:
Докажем второе утверждение.
Две фигуры называются
равными, если они движением переводятся одна в другую. Следовательно,
нужно доказать, что эти многоугольники совмещаются движением.∆А1А2А3 = ∆В1В2В3 по первому признаку (А1А2 = В1В2, А2А3 = В2В3,
<А1А2А3 = <В1В2В3). Значит, существует движение, при котором А1 → В1, А2 → В2, А3 → В3.
Подвергнем Р1 движению: А1 → В1, А2 → В2, А3 → В3, А4 → С.
Точки С и В4 лежат по одну сторону от прямой В2В3.
Движение сохраняет углы и расстояние: <В2В3С = <В2В3В4 и В3С = В3В4.
А значит, точка С совпадает с В4 и т. д. А4 → В4, А5 → В5 … Аn → Вn.
То есть Р1 → Р2 при движении, следовательно, Р1 = Р2.
I. Докажем, что Р1 → Р2.
Подвергнем Р1 преобразованию подобия: гомотетии с коэффициентом k =
Р1 → Р´ (стороны Р´ равны сторонам Р2).
Значит, Р´ → Р2 ( в результате движения).
Р1 → Р´, Р´ → Р2. Следовательно, Р1 → Р2 и т. д.
У подобных фигур
где P1, P2 – периметры, R1, R2, r1, r2 – радиусы.
Слайд 6
Решение задач
Выполнить № 32 стр.181.
Задача 1. Сторона
одного квадрата в 3 раза больше стороны другого квадрата.
Как относятся радиусы окружностей, описанных около них и вписанных в них? Ответ объясните.3) Задача 2. Дан равносторонний треугольник. Как относятся радиусы окружностей, вписанных в данный треугольник, и треугольник, вершинами которого является середина сторон данного равностороннего треугольника?