Что такое findslide.org?

FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.

Для правообладателей

Обратная связь

Email: Нажмите что бы посмотреть 

Яндекс.Метрика

Презентация на тему по геометрии на тему Квадрат

Содержание

Квадрат
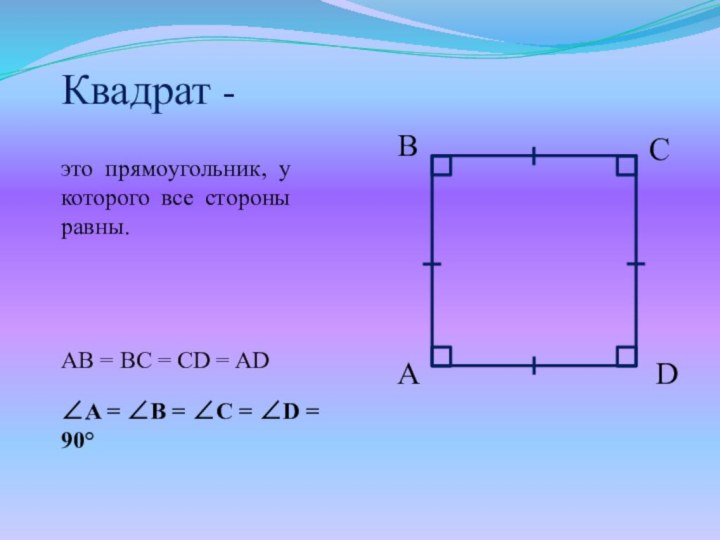
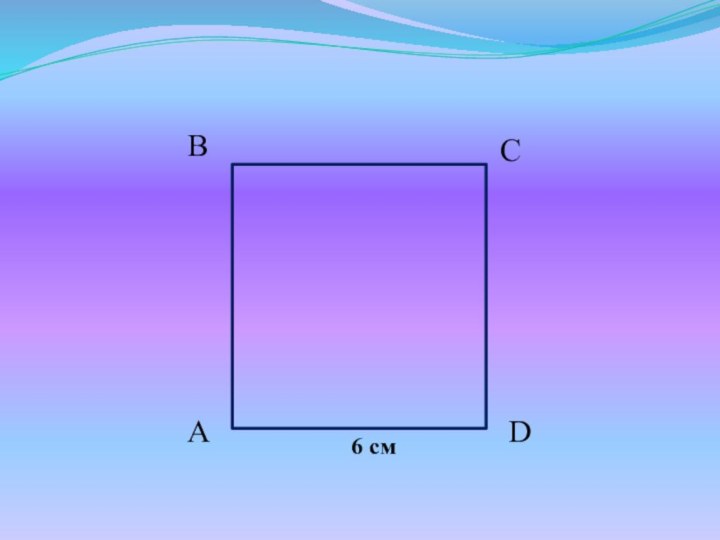
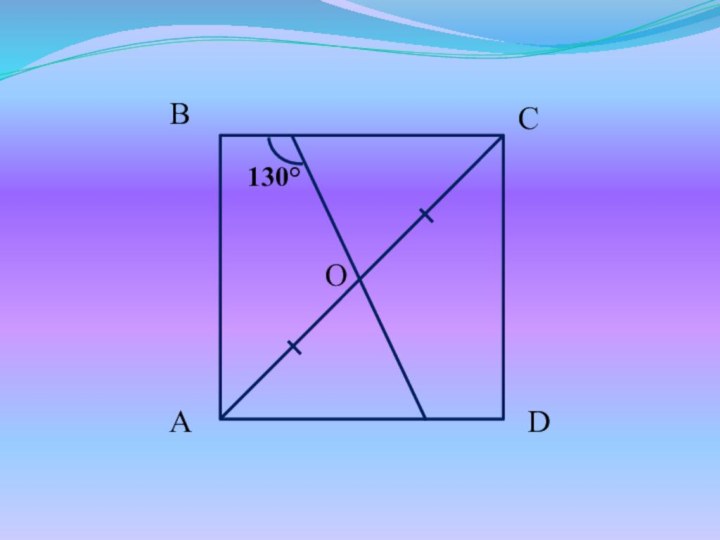
Департамент образования города Москвы Северо-Западное окружное управление образованияПрезентация по геометрии на тему Квадрат Квадрат - это прямоугольник, у которого все стороны равны.AB = BC = Задачи для устного решенияНайдите периметр квадрата ABCD. Свойства квадрата:Все свойства параллелограмма.Все свойства прямоугольника.Все свойства ромба. Задачи для устного решенияНайдите все неизвестные углы. 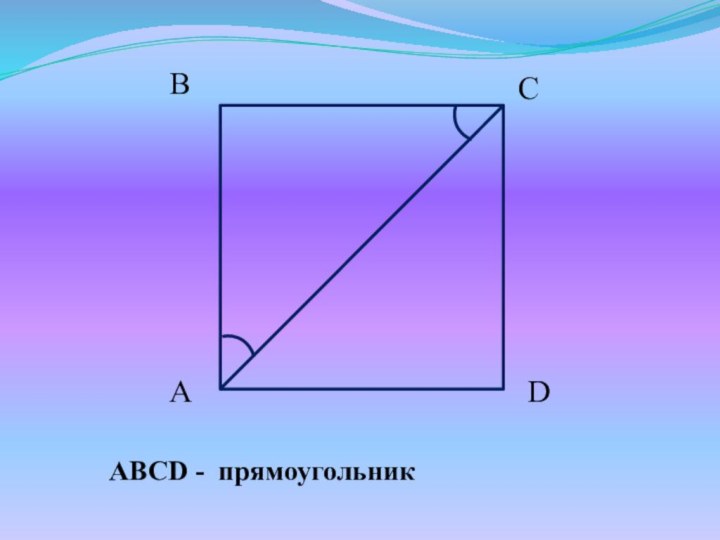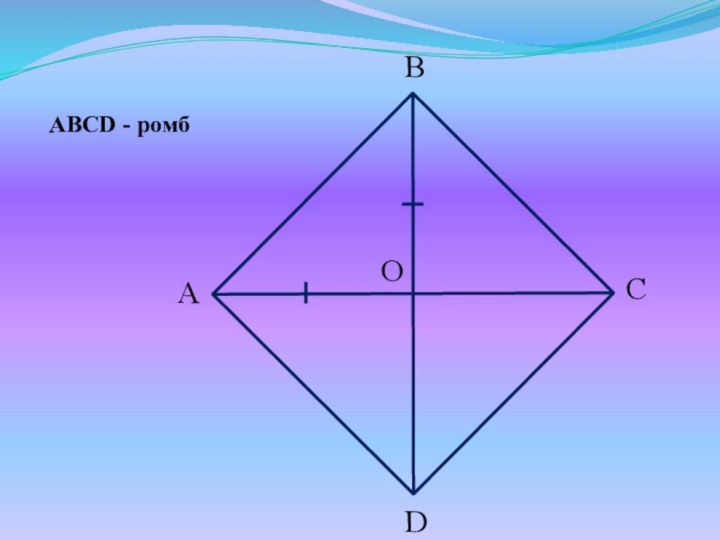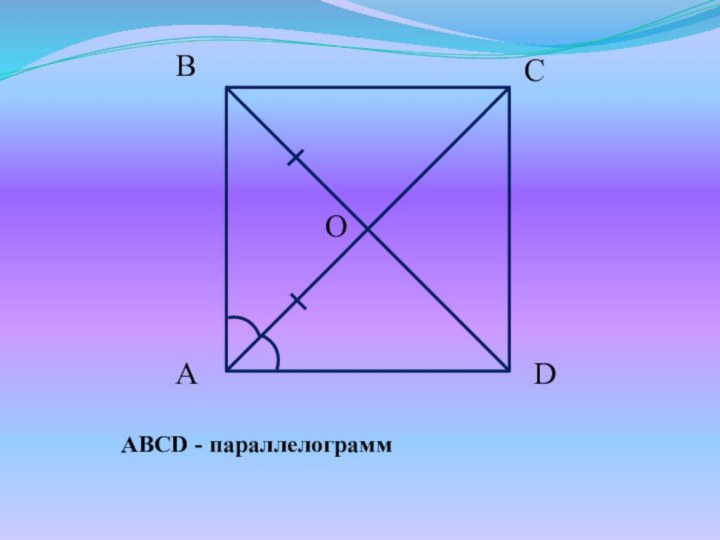130 Признаки квадрата:Если четырехугольник является прямоугольником и у него стороны равны, то это Задачи для устного решенияДокажите, что ABCD - квадрат ABCD - прямоугольник ABCD - ромб ABCD - параллелограмм Задачи для самостоятельного решения №1. Доказать, что прямоугольник, у которого диагонали перпендикулярны, является квадратом. 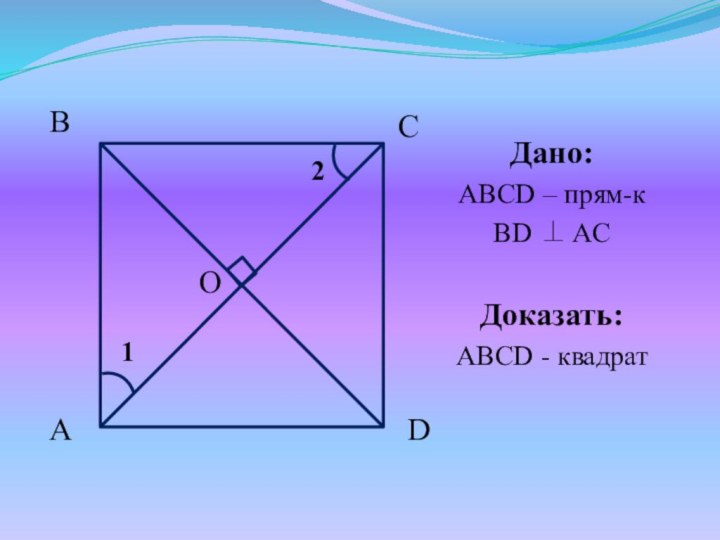Дано:ABCD – прям-кBD  ACДоказать:ABCD - квадрат12 Доказательство:Рассмотрим ΔABO и ΔСBO – прямоуг. (AC  BD): BO – общая AO №2. Периметр квадрата равен 36 см. 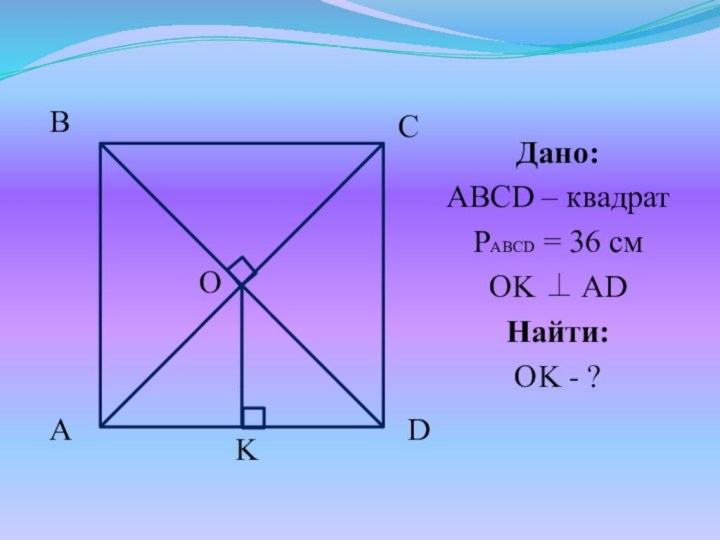Определить расстояние от точки пересечения диагоналей Дано:ABCD – квадратPABCD = 36 смOK  AD Найти:OK - ?K Решение:AC ∩ BD = O, AO = OD (свойство квадрата) ΔAOD – №3. 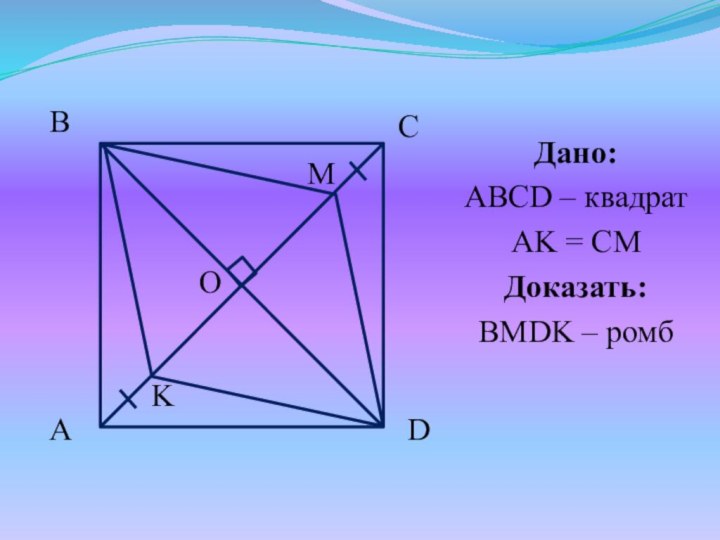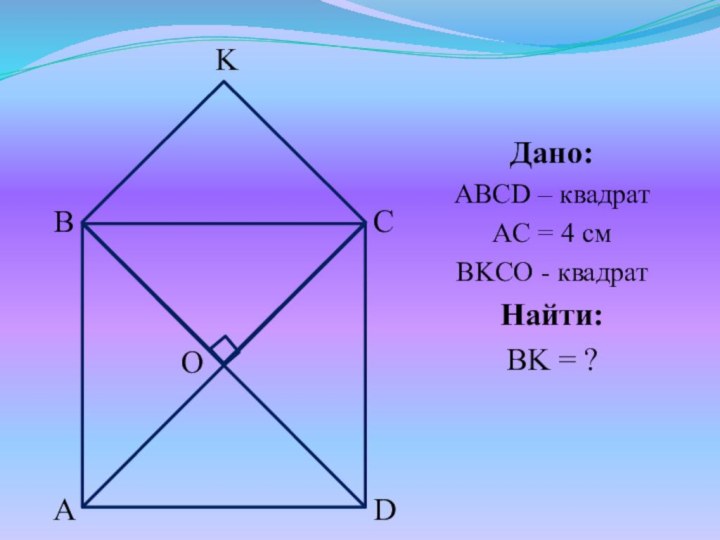На диагонали AC квадрата ABCD выбраны точки K и M такие, Дано:ABCD – квадратAK = CMДоказать:BMDK – ромбKM Доказательство:AO = OC, AK = CM => KO = OMBO = OD, №4. Диагональ квадрата равна 4 см. Его сторона является диагональю другого квадрата, определить сторону второго квадрата. Дано:ABCD – квадратAC = 4 смBKCO - квадратНайти:BK = ? Решение:BD ∩ AC = O, AO = OC = BO = OD
Слайды презентации

Слайд 2 Квадрат

Квадрат

Слайд 3 Квадрат -
это прямоугольник, у которого все стороны

Квадрат - это прямоугольник, у которого все стороны равны.AB = BC

равны.



AB = BC = CD = AD
A
B
C
D
A = B

= C = D = 90

Слайд 4 Задачи для устного решения
Найдите периметр квадрата ABCD.

Задачи для устного решенияНайдите периметр квадрата ABCD.

Слайд 5

Слайд 6

Слайд 7

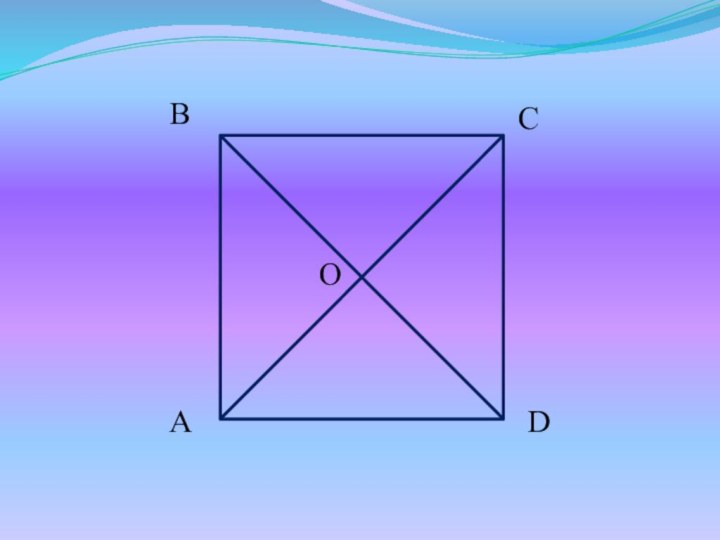
Слайд 8 Свойства квадрата:
Все свойства параллелограмма.
Все свойства прямоугольника.
Все свойства ромба.

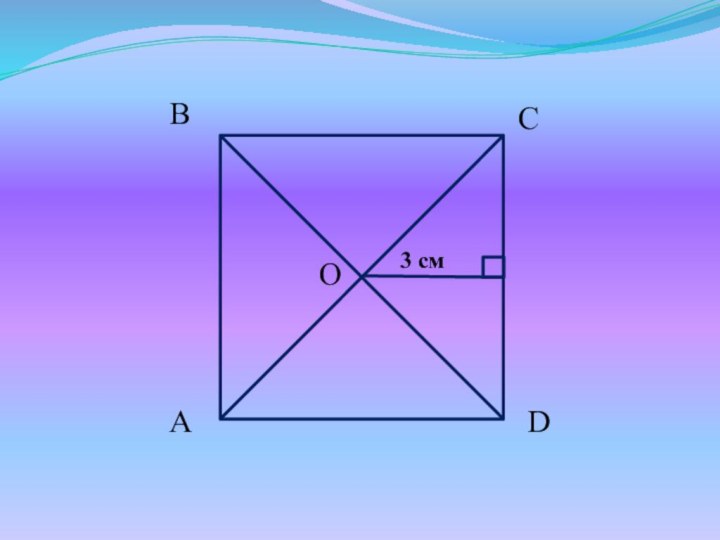
Свойства квадрата:Все свойства параллелограмма.Все свойства прямоугольника.Все свойства ромба.

Слайд 9 Задачи для устного решения
Найдите все неизвестные углы.

Задачи для устного решенияНайдите все неизвестные углы.

Слайд 10

Слайд 11

Слайд 12 130

130

Слайд 13 Признаки квадрата:
Если четырехугольник является прямоугольником и у него

Признаки квадрата:Если четырехугольник является прямоугольником и у него стороны равны, то

стороны равны, то это квадрат.
Если четырехугольник является ромбом и

у него все углы прямые, то это квадрат.

Слайд 14 Задачи для устного решения
Докажите, что ABCD - квадрат

Задачи для устного решенияДокажите, что ABCD - квадрат

Слайд 15 ABCD - прямоугольник

ABCD - прямоугольник

Слайд 16 ABCD - ромб

ABCD - ромб

Слайд 17 ABCD - параллелограмм

ABCD - параллелограмм

Слайд 18 Задачи для самостоятельного решения

Задачи для самостоятельного решения

Слайд 19 №1. Доказать, что прямоугольник, у которого диагонали перпендикулярны,

№1. Доказать, что прямоугольник, у которого диагонали перпендикулярны, является квадратом.

является квадратом.

Слайд 20
Дано:
ABCD – прям-к
BD  AC

Доказать:
ABCD - квадрат
1
2

Дано:ABCD – прям-кBD  ACДоказать:ABCD - квадрат12

Слайд 21 Доказательство:
Рассмотрим ΔABO и ΔСBO – прямоуг. (AC 

Доказательство:Рассмотрим ΔABO и ΔСBO – прямоуг. (AC  BD): BO –

BD): BO – общая AO = CO (свойство прям-ка)

=> ΔABO = ΔСBO (по двум катетам)
ΔABO = ΔСBO, зн. 1 = 2 => ΔABС – равноб. Зн. AB = BC
AB = CD, BC = AD (свойство прям-ка) AB = BC => ABCD – квадрат (по определению)

ч.т.д.

Слайд 22 №2. Периметр квадрата равен 36 см. Определить расстояние

№2. Периметр квадрата равен 36 см. Определить расстояние от точки пересечения

от точки пересечения диагоналей квадрата до его сторон.

Слайд 23
Дано:
ABCD – квадрат
PABCD = 36 см
OK  AD

Дано:ABCD – квадратPABCD = 36 смOK  AD Найти:OK - ?K


Найти:
OK - ?
K

Слайд 24 Решение:
AC ∩ BD = O, AO = OD

Решение:AC ∩ BD = O, AO = OD (свойство квадрата) ΔAOD

(свойство квадрата) ΔAOD – равноб., OK  AD =>

OK – бис., медиана
AC – бис. A, A = 90, OAK = 45, AOD = 90, AOK = 45 Зн. ΔAOK – равноб. => OK = AK = ½ AD
PABCD = 4 AB = 36 см, AB = 9 см
OK = ½ AD = ½ 9 = 4.5 см

Ответ: 4.5 см.

Слайд 25 №3. На диагонали AC квадрата ABCD выбраны точки

№3. На диагонали AC квадрата ABCD выбраны точки K и M

K и M такие, что AK = CM. Доказать,

что BMDK – ромб.

Слайд 26
Дано:
ABCD – квадрат
AK = CM
Доказать:
BMDK – ромб
K
M

Дано:ABCD – квадратAK = CMДоказать:BMDK – ромбKM

Слайд 27 Доказательство:
AO = OC, AK = CM => KO

Доказательство:AO = OC, AK = CM => KO = OMBO =

= OM
BO = OD, KO = OM => BMDK

– пар-м (по признаку)
Рассмотрим ΔBKA и ΔDKA: KA – общая AB = AD (свойство кв-та) => ΔBKA = ΔDKA BAK = DAK (свойство кв-та) (по I признаку) Зн. BK = KD
BM = KD, KB = MD (свойство пар-ма), BK = KD => BMDK – ромб (по определению)

ч.т.д.

Слайд 28 №4. Диагональ квадрата равна 4 см. Его сторона

№4. Диагональ квадрата равна 4 см. Его сторона является диагональю другого квадрата, определить сторону второго квадрата.

является диагональю другого квадрата, определить сторону второго квадрата.

Слайд 29
Дано:
ABCD – квадрат
AC = 4 см
BKCO - квадрат
Найти:
BK

Дано:ABCD – квадратAC = 4 смBKCO - квадратНайти:BK = ?
  • Имя файла: prezentatsiya-po-geometrii-na-temu-kvadrat.pptx
  • Количество просмотров: 187
  • Количество скачиваний: 0
- Предыдущая Портфолио студента
Следующая - Презентация по биологии на тему ПОДЦАРСТВО НАСТОЯЩИЕ БАКТЕРИИ (7 класс УМК Н.И. Сонин)

Похожие презентации

Актуализация Актуализация 135
Презентация по геометрии Прямоугольник, ромб, квадрат (8 кл) Презентация по геометрии Прямоугольник, ромб, квадрат (8 кл) 204
Геометрия в архитектуре древнерусского зодчества Геометрия в архитектуре древнерусского зодчества 212
Презентация по геометрии 9 класс на тему: Соотношения между сторонами и углами треугольника. Презентация по геометрии 9 класс на тему: Соотношения между сторонами и углами треугольника. 195
Тест с самопроверкой по геометрии на тему Касательная к окружности Тест с самопроверкой по геометрии на тему Касательная к окружности 131
Вопросы по векторам и параллельному переносу. Удобно в виде презентации Вопросы по векторам и параллельному переносу. Удобно в виде презентации 166
Сфера, вписанная в многогранник Сфера, вписанная в многогранник 140
Площади фигур Площади фигур 154
Презентация к уроку Теорема Пифагора Презентация к уроку Теорема Пифагора 166
Площадь круга. Длина окружности Площадь круга. Длина окружности 188
Презентация по теме: Осевая симметрия Презентация по теме: Осевая симметрия 142
Презентация по теме Цилиндр (11 класс) Презентация по теме Цилиндр (11 класс) 161
Измерение высоты предмета Измерение высоты предмета 173
Параллельность прямой и плоскости Параллельность прямой и плоскости 234
Окружность (7 класс) Окружность (7 класс) 188
Презентация по геометрии 8 класс на тему ПЛОЩАДЬ ПАРАЛЛЕЛОГРАММА Презентация по геометрии 8 класс на тему ПЛОЩАДЬ ПАРАЛЛЕЛОГРАММА 190
Поворот Поворот 138
Презентация по геометрии на тему Сфера,шар Презентация по геометрии на тему Сфера,шар 144
Площадь параллелограмма Площадь параллелограмма 166
Презентация по геометрии История геометрии Презентация по геометрии История геометрии 169
Построение параллелограмма по двум смежным сторонам и углу между ними Построение параллелограмма по двум смежным сторонам и углу между ними 201
Средняя линия трапеции Средняя линия трапеции 195
Презентация к уроку геометрии в 10 классе Двугранный угол Презентация к уроку геометрии в 10 классе Двугранный угол 154
Сумма углов в треугольнике Сумма углов в треугольнике 128
Координатный метод в пространстве Координатный метод в пространстве 166
Площадь многоугольников Площадь многоугольников 140
Презентация для интегрированного урока математики и информатики по теме Теорема Пифагора Презентация для интегрированного урока математики и информатики по теме Теорема Пифагора 171
Правила сложения и вычитания векторов Правила сложения и вычитания векторов 204
Понятие цилиндра Понятие цилиндра 49
Правильные многогранники в жизни Правильные многогранники в жизни 222