Что такое findslide.org?

FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.

Обратная связь

Презентация на тему по геометрии Теорема Пифагора (8 класс)

Содержание

2. Цель урока: Закрепить умение применять теорему Пифагора
3. Математический диктант 1. Какой треугольник называется прямоугольным?2.
4. Проверка математического диктанта 1. Если есть прямой
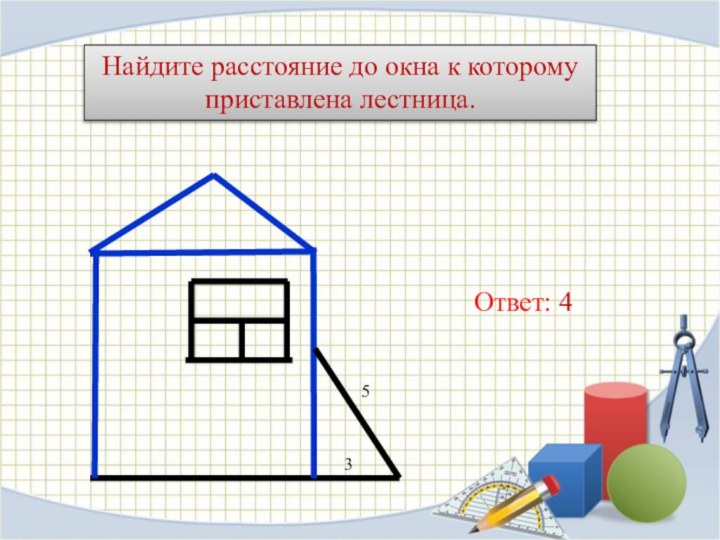
5. Найдите расстояние до окна к которому приставлена лестница. 53Ответ: 4
6. Задача 1Боковые стороны равнобедренного треугольника равны 10.
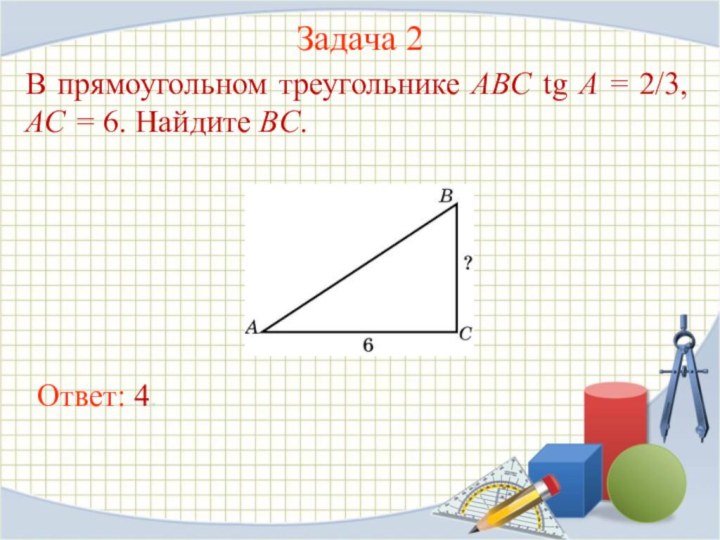
7. Задача 2В прямоугольном треугольнике ABC tg A = 2/3, AC = 6. Найдите BC.Ответ: 4.
9. Решение задачиПусть CD – высота ствола.BD = АВПо теореме Пифагора
10. Задача арабского математика 11 века про птиц
11. Решение задачиИтак, в треугольнике АDВ: АВ =ВD
12. Проверочная работа
13. Итог урока:Сформулируйте теорему Пифагора,Как найти катет прямоугольного треугольника, зная гипотенузу и другой катет.
14. Домашнее задание:1. По карточкам решить старинную задачу из китайской «Математики в девяти книгах» 2. Разгадать кроссворд
15. «СЕГОДНЯ НА УРОКЕ Я ПОВТОРИЛ……..» «СЕГОДНЯ
16. Интернет-ресурсыhttp://www.univer.omsk.su/omsk/Edu/Math/ppifagor.jpg2. http://www.abc-people.com/data/rafael-santi/pic-8b.jpg3. Учебник «Геометрия» 7-9 кл., Атанасян Л.С., -М.: Просвещение.
17. Скачать презентацию
18. Похожие презентации

Цель урока: Закрепить умение применять теорему Пифагора при решении задачРазвивать логическое мышлениеУчить использовать полученные знания на практике и в повседневной жизни

Главная
Геометрия
Презентация по геометрии Теорема Пифагора (8 класс)

ТЕОРЕМА ПИФАГОРА урок обобщения и закрепления изученного материалаАвтор: Вдовина Елена НиколаевнаУчитель математики

Цель урока: Закрепить умение применять теорему Пифагора при решении задачРазвивать логическое мышлениеУчить

Математический диктант 1. Какой треугольник называется прямоугольным?2. Чему равна сумма углов прямоугольного

Проверка математического диктанта 1. Если есть прямой угол.2. 180° 90°4. Катет прямоугольного

Найдите расстояние до окна к которому приставлена лестница. 53Ответ: 4

Задача 1Боковые стороны равнобедренного треугольника равны 10. Высота, опущенная на основание, равна

Задача 2В прямоугольном треугольнике ABC tg A = 2/3, AC = 6. Найдите BC.Ответ: 4.

Решение задачиПусть CD – высота ствола.BD = АВПо теореме Пифагора имеемАB²=AC²+BC²,АB²=9+16=25,АВ = 5 .CD = CB + BD,CD = 3

Задача арабского математика 11 века про птиц На обоих берегах реки растет

Решение задачиИтак, в треугольнике АDВ: АВ =ВD +АD АВ =30 +Х АВ

Итог урока:Сформулируйте теорему Пифагора,Как найти катет прямоугольного треугольника, зная гипотенузу и другой катет.

Домашнее задание:1. По карточкам решить старинную задачу из китайской «Математики в девяти книгах» 2. Разгадать кроссворд

«СЕГОДНЯ НА УРОКЕ Я ПОВТОРИЛ……..» «СЕГОДНЯ НА УРОКЕ Я УЗНАЛ……….»

Интернет-ресурсыhttp://www.univer.omsk.su/omsk/Edu/Math/ppifagor.jpg2. http://www.abc-people.com/data/rafael-santi/pic-8b.jpg3. Учебник «Геометрия» 7-9 кл., Атанасян Л.С., -М.: Просвещение.

источник шаблона презентации: Ранько Елена Алексеевна учитель начальных классов МАОУ лицей №21 г. Иваново

Слайды презентации

Слайд 2 Цель урока:
Закрепить умение применять теорему Пифагора при решении

Цель урока: Закрепить умение применять теорему Пифагора при решении задачРазвивать логическое

задач
Развивать логическое мышление
Учить использовать полученные знания на практике и

в повседневной жизни

Слайд 3 Математический диктант
1. Какой треугольник называется прямоугольным?
2. Чему равна

Математический диктант 1. Какой треугольник называется прямоугольным?2. Чему равна сумма углов

сумма углов прямоугольного треугольника?
3. Чему равна сумма острых углов

в прямоугольном треугольнике?
4. Сформулируйте свойство катета, лежащего против угла в 30 градусов.
5. Сформулируйте теорему Пифагора.
6. Как называется сторона противолежащая прямому углу?
7. Как называется сторона прилежащая к прямому углу?

Слайд 4 Проверка математического диктанта
1. Если есть прямой угол.
2. 180°

Проверка математического диктанта 1. Если есть прямой угол.2. 180° 90°4. Катет

90°
4. Катет прямоугольного треугольника, лежащий против угла в 30° равен

половине гипотенузы.
5. В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.
6. Гипотенуза.
7. Катет.

Слайд 5 Найдите расстояние до окна к которому приставлена лестница.

5
3
Ответ: 4

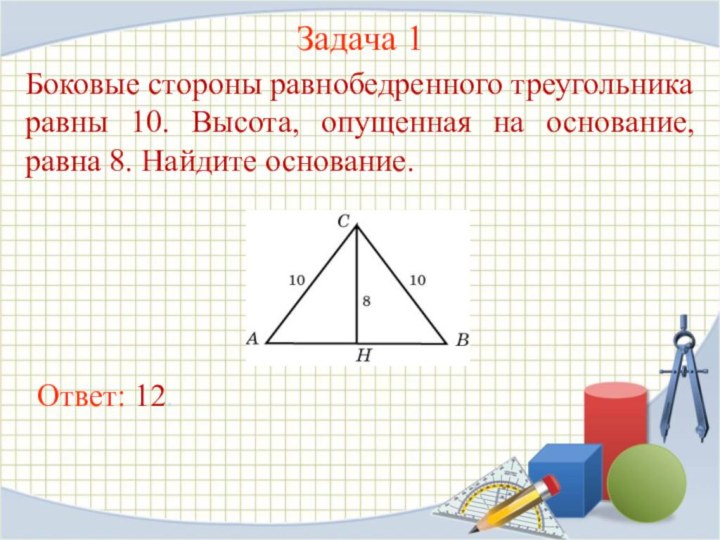
Слайд 6 Задача 1
Боковые стороны равнобедренного треугольника равны 10. Высота,

Задача 1Боковые стороны равнобедренного треугольника равны 10. Высота, опущенная на основание,

опущенная на основание, равна 8. Найдите основание.
Ответ: 12.

Слайд 7 Задача 2
В прямоугольном треугольнике ABC tg A =

2/3, AC = 6. Найдите BC.
Ответ: 4.

Слайд 8 Задача про тополь индийского математика Бхаскары.
На берегу реки

рос тополь одинокий. Вдруг ветра порыв его ствол надломал.

Бедный тополь упал. И угол прямой с теченьем реки его ствол составлял. Запомни теперь, что в том месте река в четыре лишь фута была широка. Верхушка склонилась у края реки, осталось три фута всего от ствола. Прошу тебя, скоро теперь мне скажи: у тополя как велика высота?

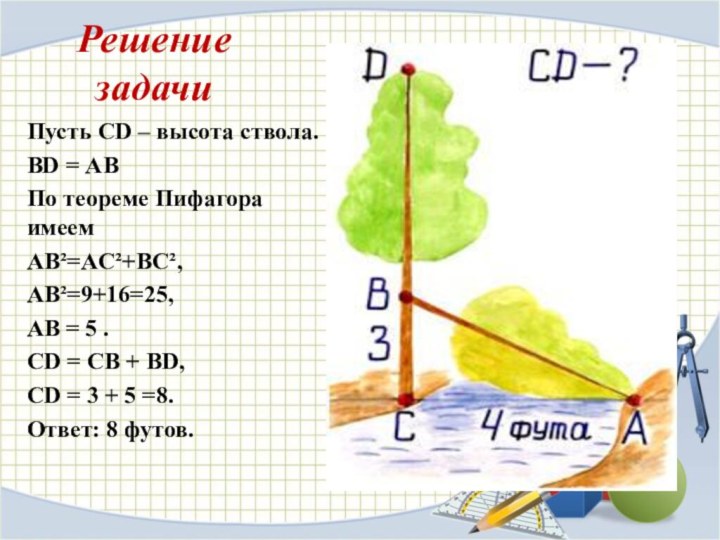
Слайд 9 Решение задачи
Пусть CD – высота ствола.
BD = АВ
По теореме Пифагора имеем
АB²=AC²+BC²,
АB²=9+16=25,
АВ

Решение задачиПусть CD – высота ствола.BD = АВПо теореме Пифагора имеемАB²=AC²+BC²,АB²=9+16=25,АВ = 5 .CD = CB + BD,CD =

= 5 .
CD = CB + BD,
CD = 3 + 5 =8.
Ответ: 8 футов.

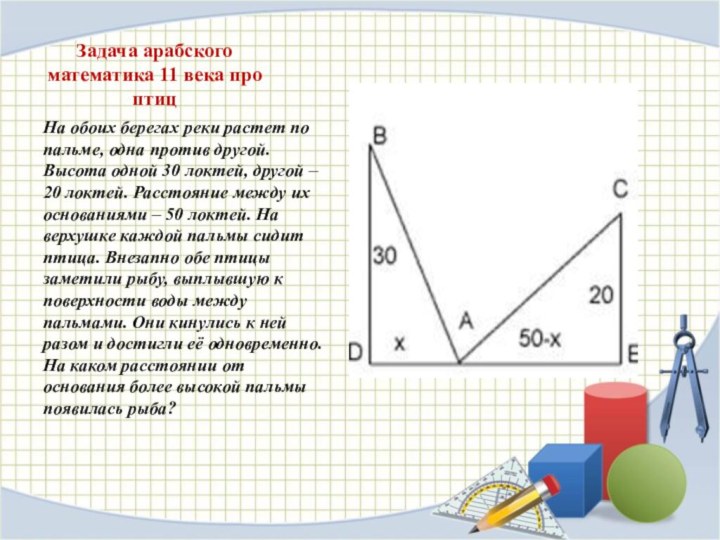
Слайд 10 Задача арабского математика 11 века про птиц
На

Задача арабского математика 11 века про птиц На обоих берегах реки

обоих берегах реки растет по пальме, одна против другой.

Высота одной 30 локтей, другой – 20 локтей. Расстояние между их основаниями – 50 локтей. На верхушке каждой пальмы сидит птица. Внезапно обе птицы заметили рыбу, выплывшую к поверхности воды между пальмами. Они кинулись к ней разом и достигли её одновременно. На каком расстоянии от основания более высокой пальмы появилась рыба?

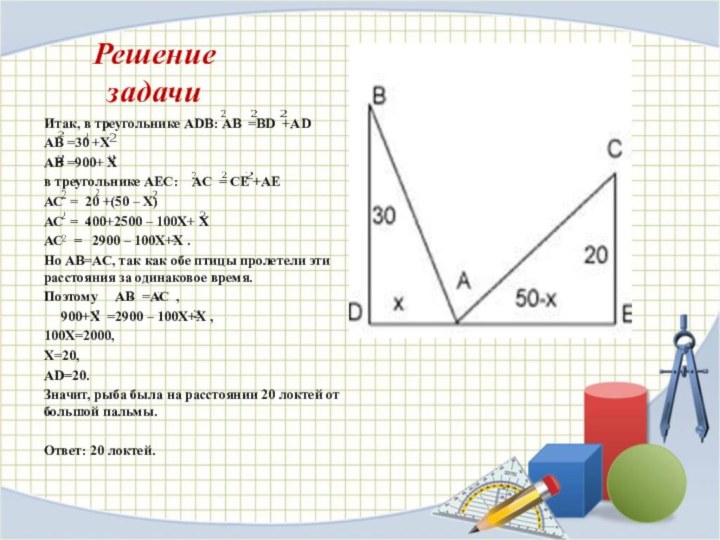
Слайд 11 Решение задачи
Итак, в треугольнике АDВ: АВ =ВD +АD

Решение задачиИтак, в треугольнике АDВ: АВ =ВD +АD АВ =30 +Х

АВ =30 +Х
АВ =900+ Х
в треугольнике АЕС:

АС = СЕ +АЕ
АС = 20 +(50 – Х)
АС = 400+2500 – 100Х+ Х
АС = 2900 – 100Х+Х .
Но АВ=АС, так как обе птицы пролетели эти расстояния за одинаковое время.
Поэтому АВ =АС ,
900+Х =2900 – 100Х+Х ,
100Х=2000,
Х=20,
АD=20.
Значит, рыба была на расстоянии 20 локтей от большой пальмы.

Ответ: 20 локтей.