Векторы называются коллинеарными, если они лежат на одной прямой
или напараллельных прямых
Определение 3. Два вектора называются равными, если они коллинеарные, имеют одинаковую длину, одинаковое направление.
a
a
b
c
а
в
с
d
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Email: Нажмите что бы посмотреть





a
a
b
c
а
в
с
d
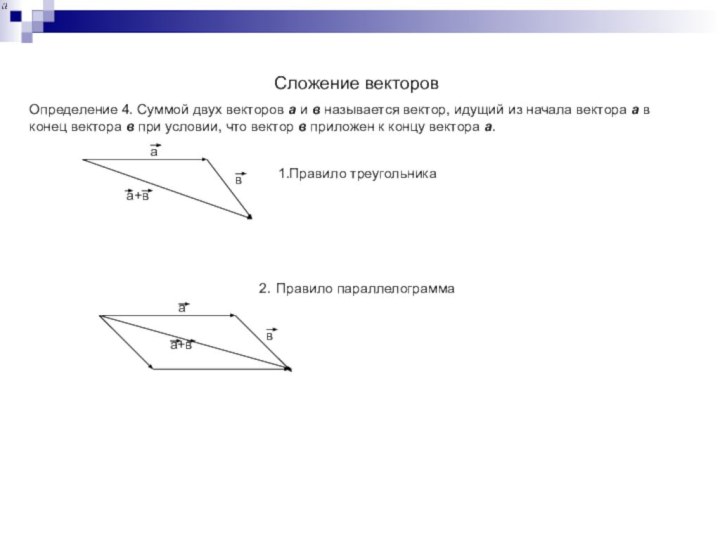
а
в
а+в
а
в
а+в
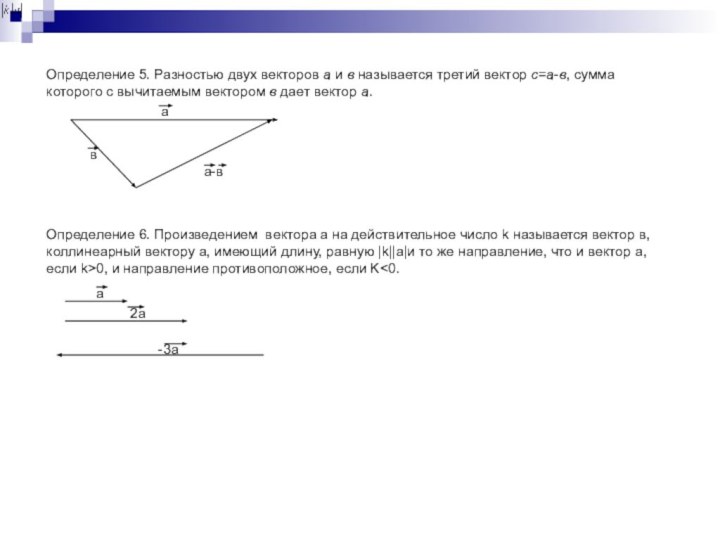
а
в
а-в
а
2а
-3а
а
в
с