- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему по геометрии на тему Параллелепипед (9 класс).
Содержание
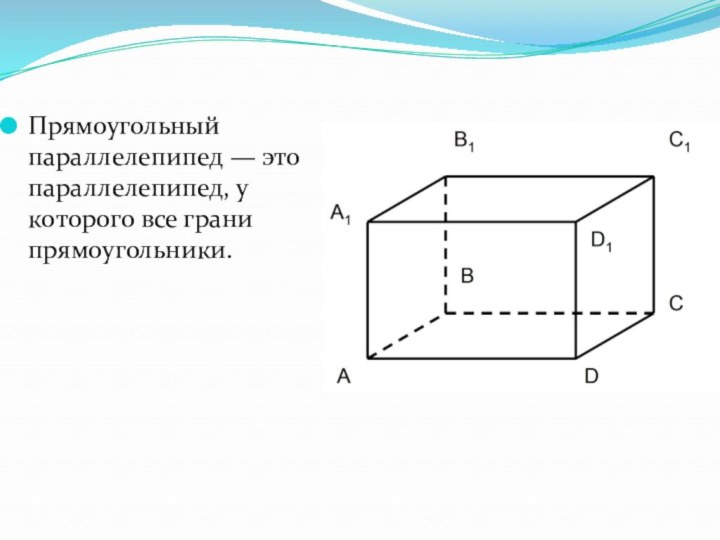
- 2. Прямоугольный параллелепипед — это параллелепипед, у которого все грани прямоугольники.
- 3. Задача №1Дан прямоугольный параллелепипед, стороны основания которого
- 4. Ответ к задаче №1Заметим, что все варианты
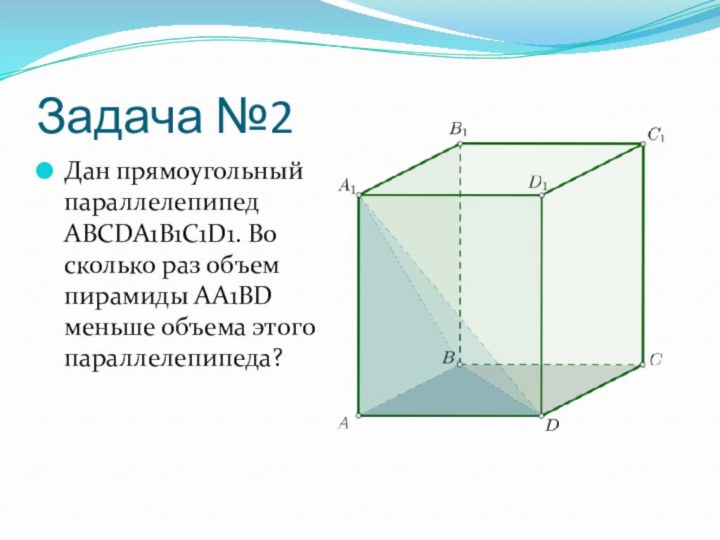
- 5. Задача №2Дан прямоугольный параллелепипед ABCDA1B1C1D1. Во сколько раз объем пирамиды AA1BD меньше объема этого параллелепипеда?
- 6. Решение задачи №2Пусть AB=x, AD=y, AA1=z.
- 7. Задача №3В прямоугольном параллелепипеде диагональ грани AA1D1D равна 5, а AB=26. Найдите диагональ параллелепипеда.
- 8. Скачать презентацию
- 9. Похожие презентации
Прямоугольный параллелепипед — это параллелепипед, у которого все грани прямоугольники.