- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Параллельные прямые
Содержание
- 2. Теорема о параллельных прямых. Через любую точку
- 3. Лемма о пересечении плоскости параллельными прямыми.Если одна
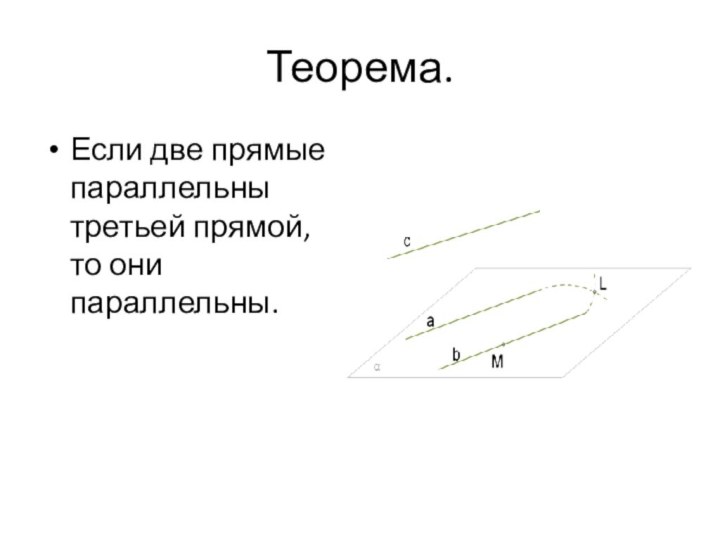
- 4. Теорема.Если две прямые параллельны третьей прямой, то они параллельны.
- 5. Параллельность прямой и плоскости.Три случая взаимного расположения
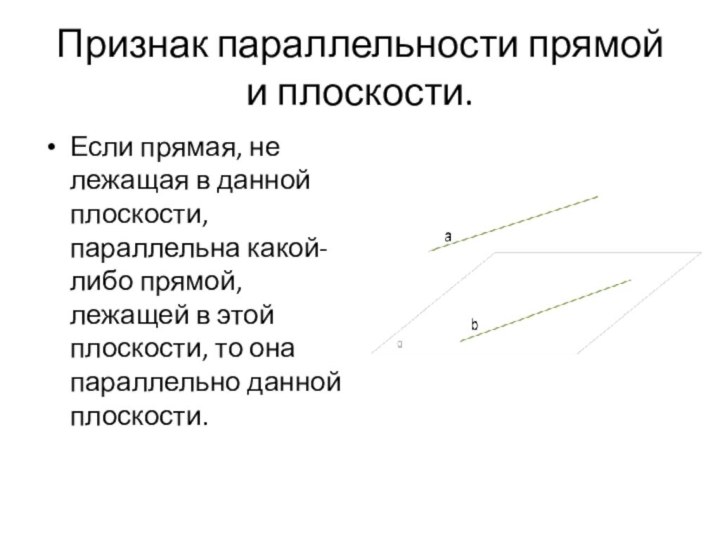
- 6. Признак параллельности прямой и плоскости.Если прямая, не лежащая
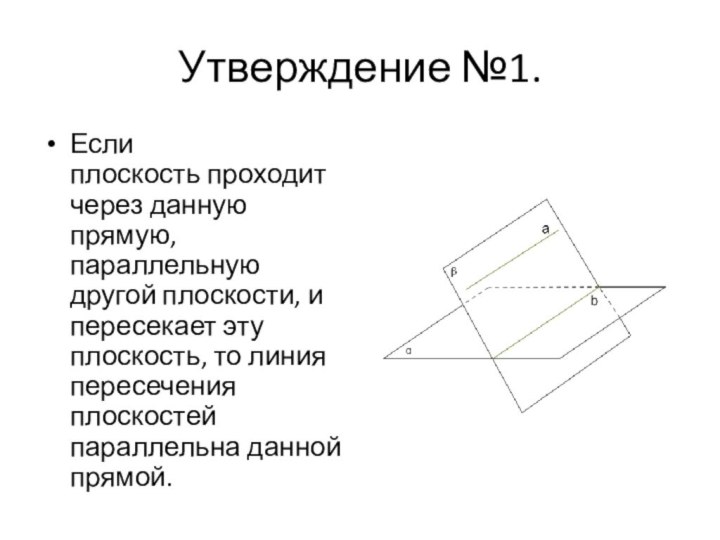
- 7. Утверждение №1.Если плоскость проходит через данную прямую, параллельную
- 8. Утверждение №2.Если одна из двух параллельных прямых параллельна
- 9. Скрещивающиеся прямые.Две прямые называются скрещивающимися, если они не лежат в одной плоскости.
- 10. Теорема «Признак скрещивающихся прямых».Если одна из двух
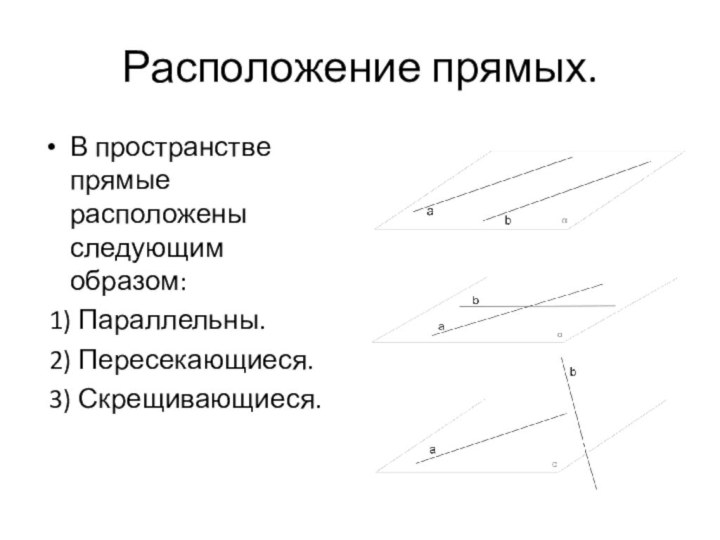
- 11. Расположение прямых.В пространстве прямые расположены следующим образом: 1) Параллельны. 2) Пересекающиеся. 3) Скрещивающиеся.
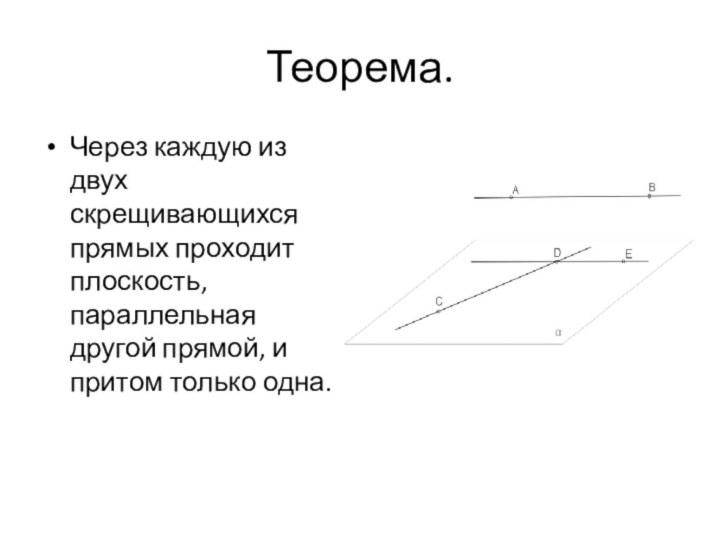
- 12. Теорема.Через каждую из двух скрещивающихся прямых проходит плоскость, параллельная другой прямой, и притом только одна.
- 13. Углы с сонаправленными сторонами.Два луча, не лежащие
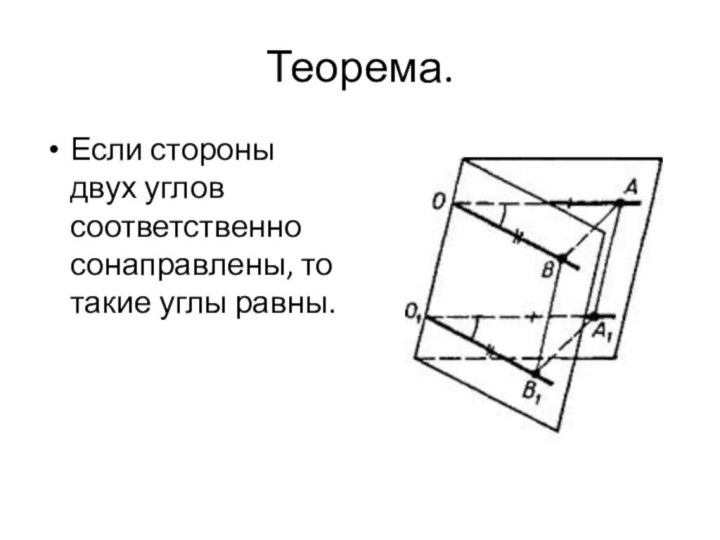
- 14. Теорема.Если стороны двух углов соответственно сонаправлены, то такие углы равны.
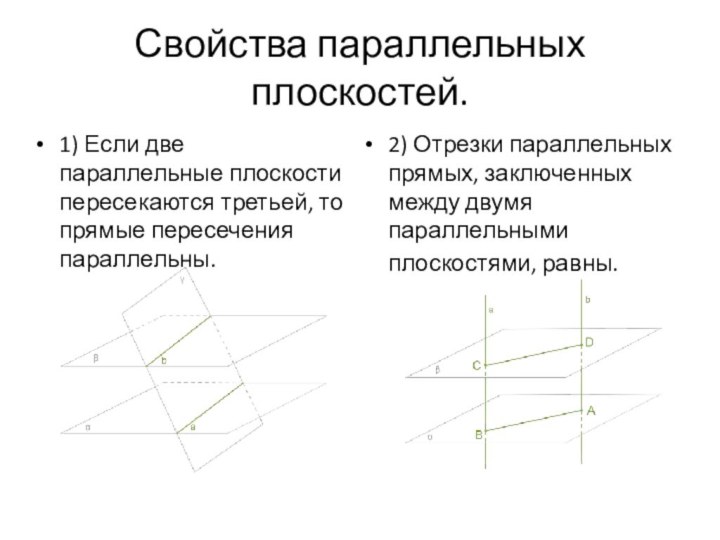
- 15. Параллельные плоскости.Две плоскости называют параллельными, если они не пересекаются.
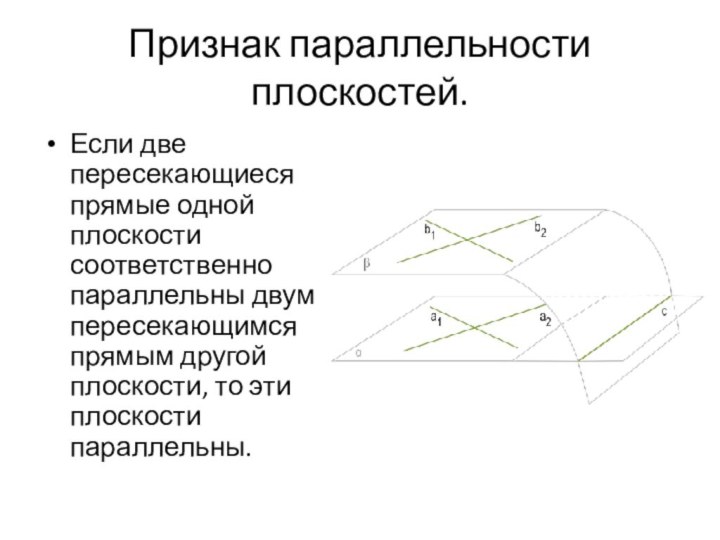
- 16. Признак параллельности плоскостей.Если две пересекающиеся прямые одной
- 17. Скачать презентацию
- 18. Похожие презентации
Теорема о параллельных прямых. Через любую точку пространства, не лежащую на данной прямой, проходят прямая, параллельная данной , и притом только одна.








Слайд 3
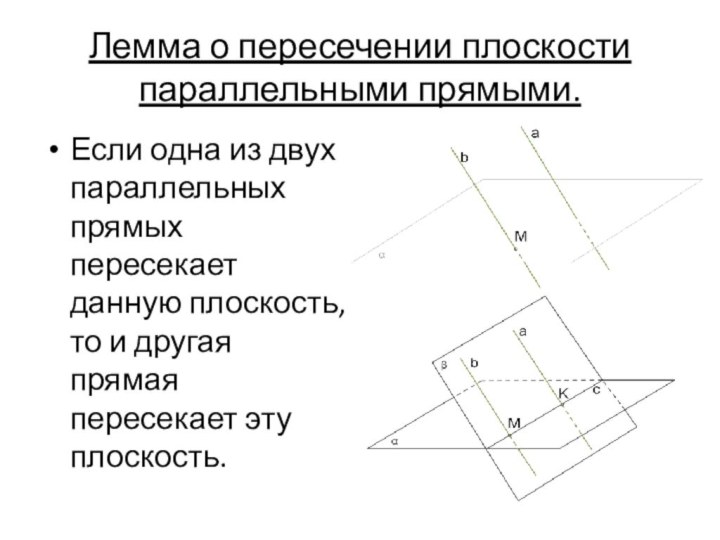
Лемма о пересечении плоскости параллельными прямыми.
Если одна из
двух параллельных прямых пересекает данную плоскость, то и другая
прямая пересекает эту плоскость.
Слайд 5
Параллельность прямой и плоскости.
Три случая взаимного расположения прямой
и плоскости в пространстве:
1)Прямая лежит в плоскости.
2)Прямая и плоскость
имеют только одну общую точку (т.е. пересекаются).3)Прямая и плоскость не имеют ни одной общей точки.
Прямая и плоскость называются параллельными, если они не имеют общих точек.