Презентация на тему Ортотреугольник и его свойства

Дей Тоски (1682—1766)
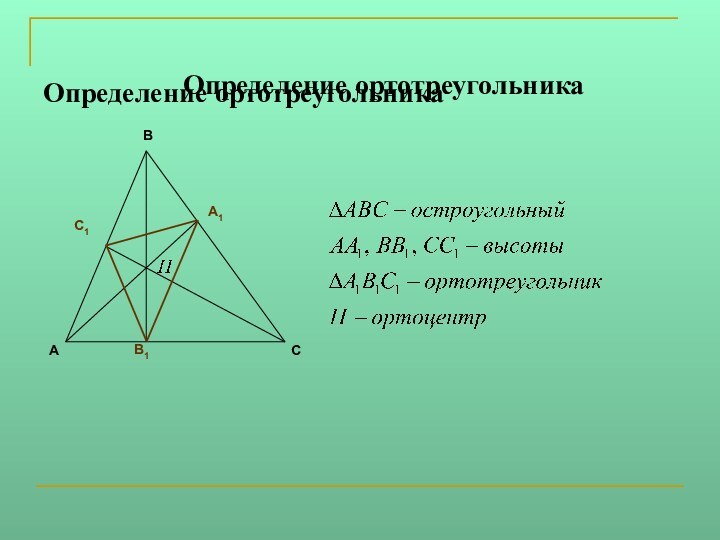
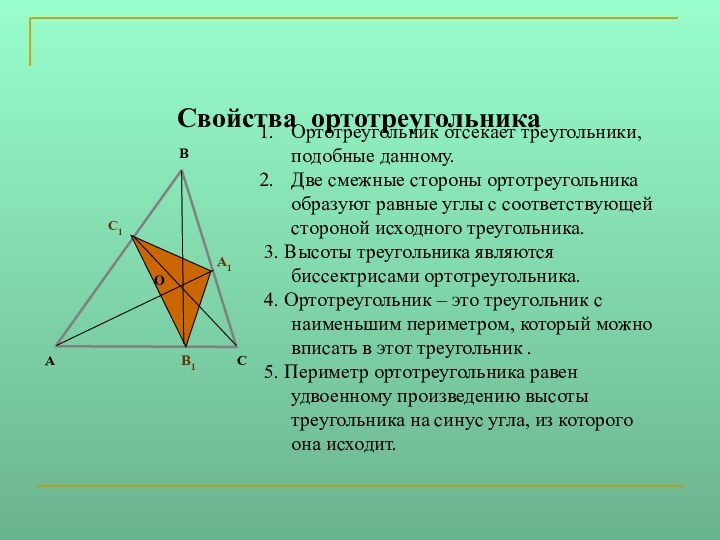
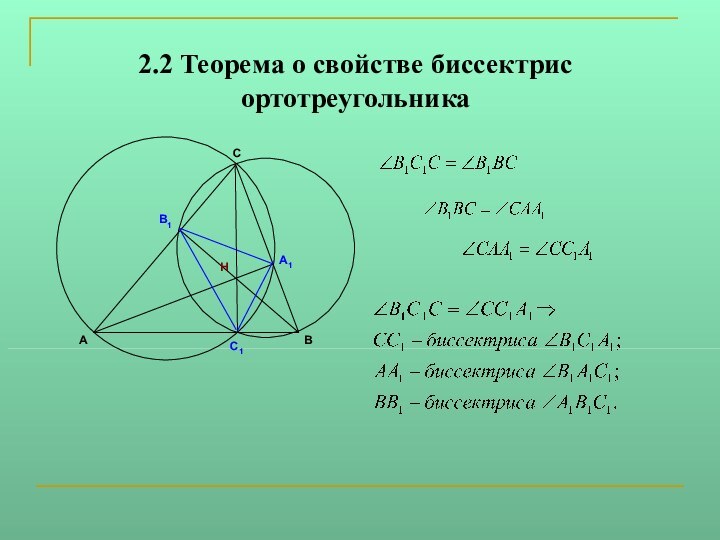
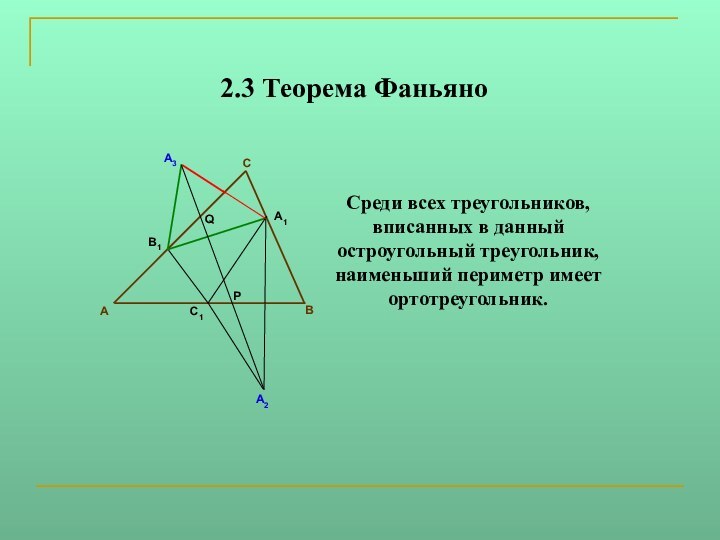
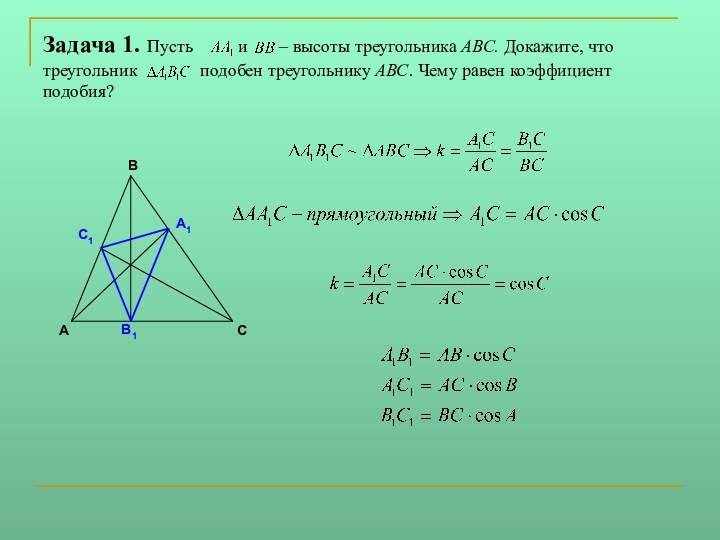
Задача: вписать в данный остроугольный треугольник

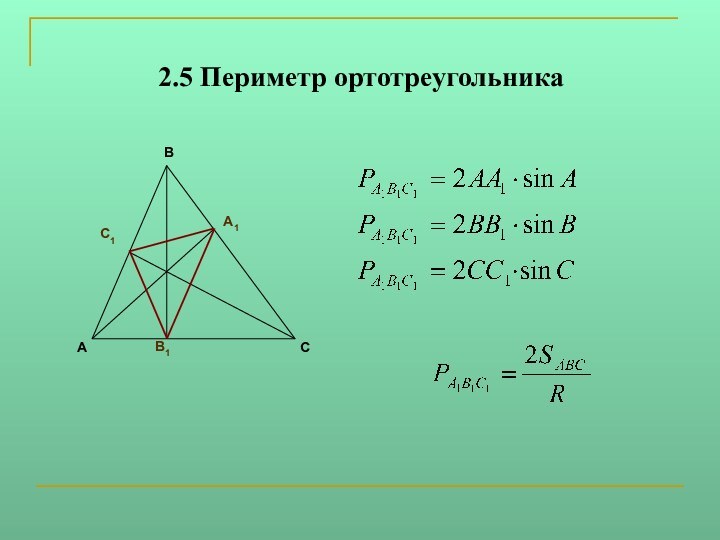
ABC треугольник наименьшего периметра так, чтобы на каждой стороне треугольника ABC лежала одна вершина треугольника.
Существует единственный вписанный треугольник наименьшего периметра - ортотреугольник.

выяснить, что такое ортотреугольник;
2) изучить его свойства;
3) рассмотреть возможное

применение
этих свойств к решению задач.

ортотреугольника образуют равные углы с соответствующей стороной исходного треугольника.
3.

Высоты треугольника являются биссектрисами ортотреугольника.
4. Ортотреугольник – это треугольник с наименьшим периметром, который можно вписать в этот треугольник .
5. Периметр ортотреугольника равен удвоенному произведению высоты треугольника на синус угла, из которого она исходит.

подобные данному.

остроугольный треугольник, наименьший периметр имеет ортотреугольник.

– высоты треугольника АВС. Докажите, что

треугольник подобен треугольнику АВС. Чему равен коэффициент подобия?

АD, ВЕ и СF.Докажите, что pR=Pr, где p-периметр треугольника

EDF, Р – периметр треугольника АВС.