- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Теорема Пифагора для прямоугольного треугольника
Содержание
- 2. Пифагор Самосский — древнегреческий философ, математик и мистик, создатель религиозно -философской школы пифагор -
- 3. Ещё Геродот называл его «величайшим эллинским мудрецом».Самые ранние известные
- 5. Учение Пифагора следует разбить на две составляющие
- 6. Монета с изображением ПифагораВ современном мире Пифагор
- 7. Античные авторы нашей эры отдают Пифагору авторство известной теоремы:
- 8. Изначально теорема была сформулирована следующим образом: или:Обе
- 10. Пусть ABC есть прямоугольный треугольник с прямым углом C.
- 11. Трудно найти человека, у которого имя Пифагора
- 12. Это сочетание двух противоречивых начал и придает
- 13. Скачать презентацию
- 14. Похожие презентации
Пифагор Самосский — древнегреческий философ, математик и мистик, создатель религиозно -философской школы пифагор - ейцев.Историю жизни Пифагора трудно отделить от легенд, представляющих его в качестве совершенного мудреца и великого посвящённого во все таинства греков и варваров.











Слайд 2
Пифагор Самосский — древнегреческий философ, математик и мистик, создатель религиозно -философской школы пифагор - ейцев.
Историю
Слайд 3
Ещё Геродот называл его «величайшим эллинским мудрецом».
Самые ранние известные источники
об учении Пифагора появились лишь 200 лет спустя после
его смерти. Сам Пифагор не оставил сочинений, и все сведения о нём и его учении основываются на трудах его последователей, не всегда беспристрастных.В честь Пифагора назван кратер на Луне.
Слайд 5 Учение Пифагора следует разбить на две составляющие части:
научный подход к познанию мира и религиозно-мистический образ жизни,
проповедуемый Пифагором. Доподлинно неизвестны заслуги Пифагора в первой части, так как ему позднее приписывали всё, созданное последователями в рамках школы пифагореизма. Вторая часть превалирует в учении Пифагора, и именно она осталась в сознании большинства античных авторов.
Слайд 6
Монета с изображением Пифагора
В современном мире Пифагор считается
великим математиком и космологом древности, однако ранние свидетельства до III
в. до н. э. не упоминают о таких его заслугах. Как пишет Ямвлих про пифагорейцев: «У них также был замечательный обычай приписывать всё Пифагору и нисколько не присваивать себе славы первооткрывателей, кроме, может быть, нескольких случаев.»Слайд 7 Античные авторы нашей эры отдают Пифагору авторство известной теоремы: квадрат
гипотенузы прямоугольного треугольника равняется сумме квадратов катетов. Такое мнение
основывается на сведениях Аполлодора - исчислителя (личность не идентифицирована) и на стихотворных строках (источник стихов не известен):«В день, когда Пифагор открыл свой чертёж знаменитый, Славную он за него жертву быками воздвиг.»
Слайд 8
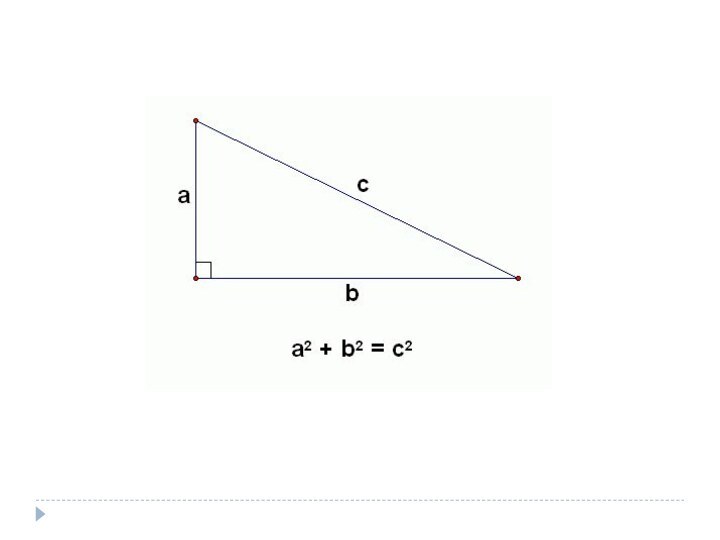
Изначально теорема была сформулирована следующим образом:
или:
Обе формулировки
теоремы эквивалентны, но вторая формулировка более элементарна, она не
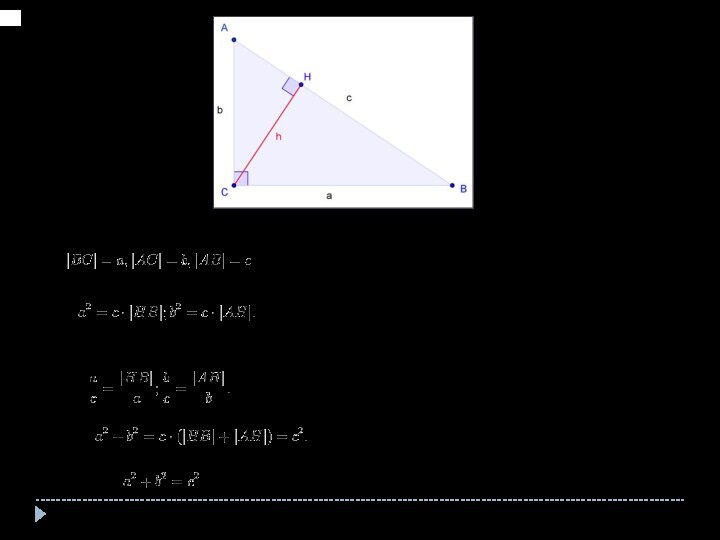
требует понятия площади. То есть второе утверждение можно проверить, ничего не зная о площади и измерив только длины сторон прямоугольного треугольника.Слайд 10 Пусть ABC есть прямоугольный треугольник с прямым углом C. Проведём
высоту из C и обозначим её основание через H. Треугольник ACH подобен треугольнику ABC по двум углам.
Аналогично, треугольник CBH подобен ABC. Введя обозначения:Получаем:
Что эквивалентно
Сложив, получаем
или
, что и требовалось доказать