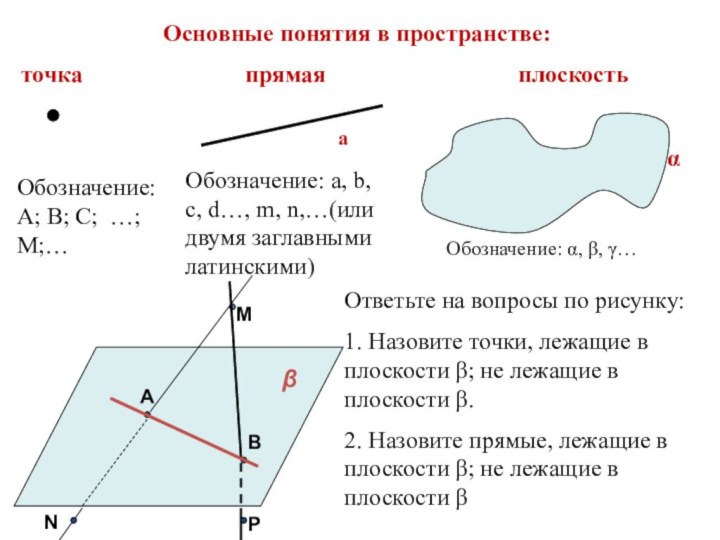
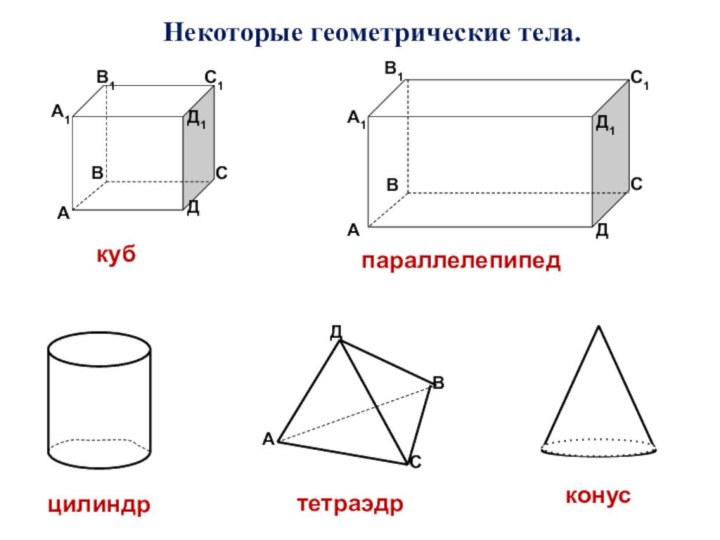
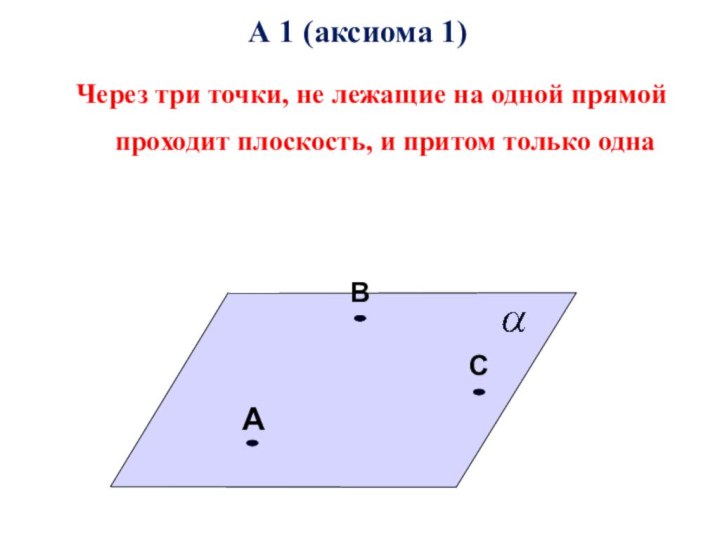
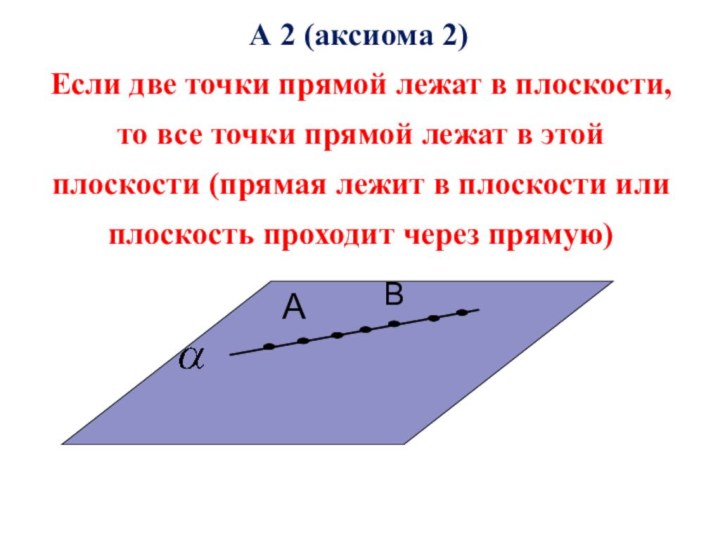
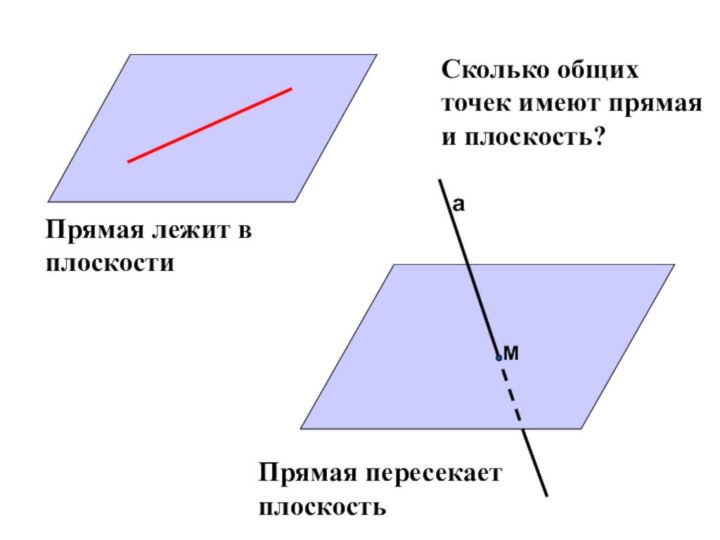
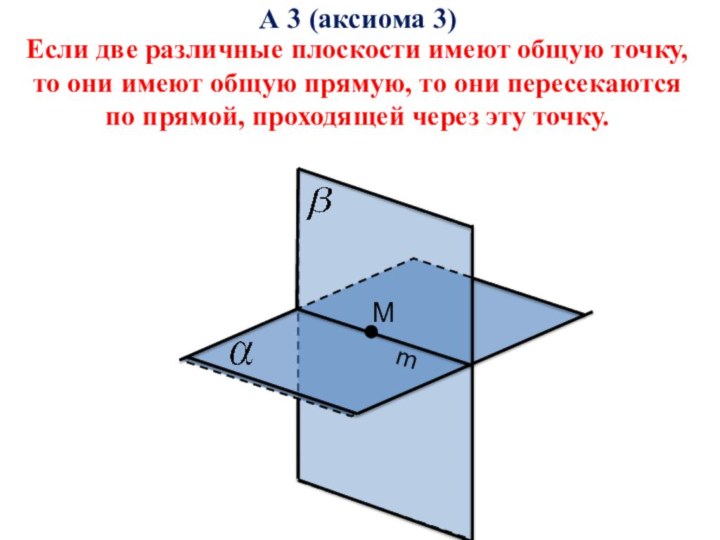
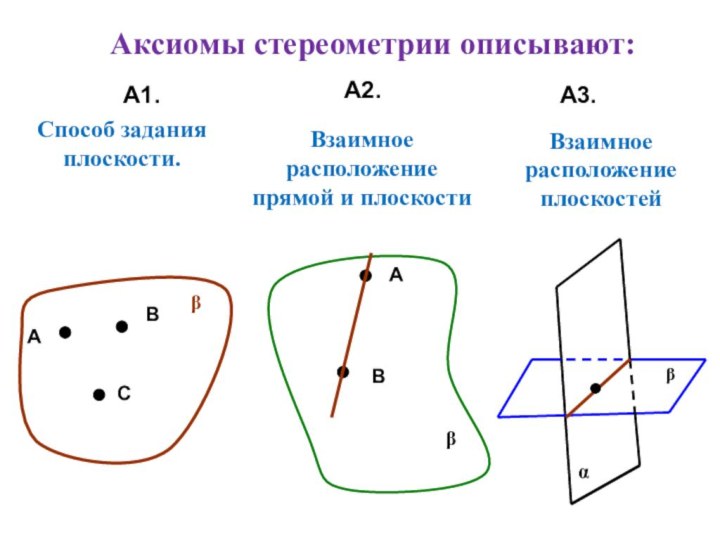
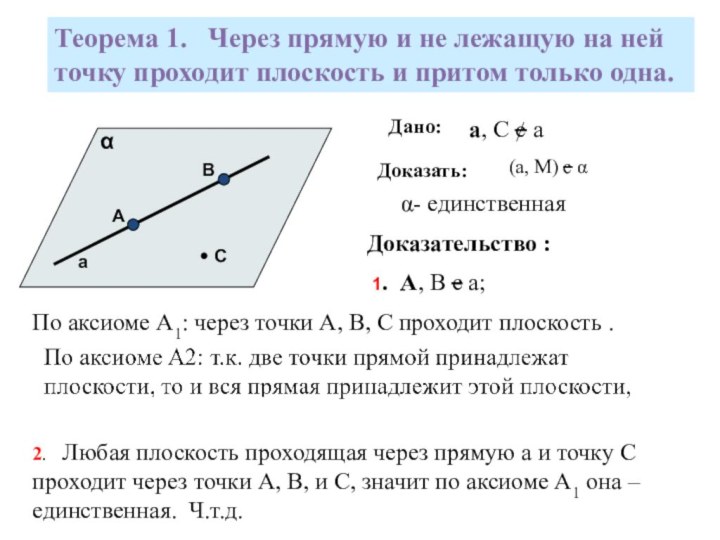
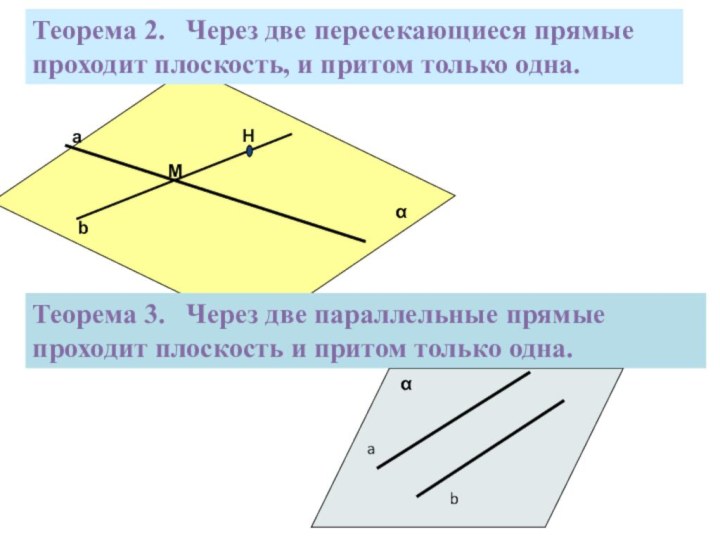
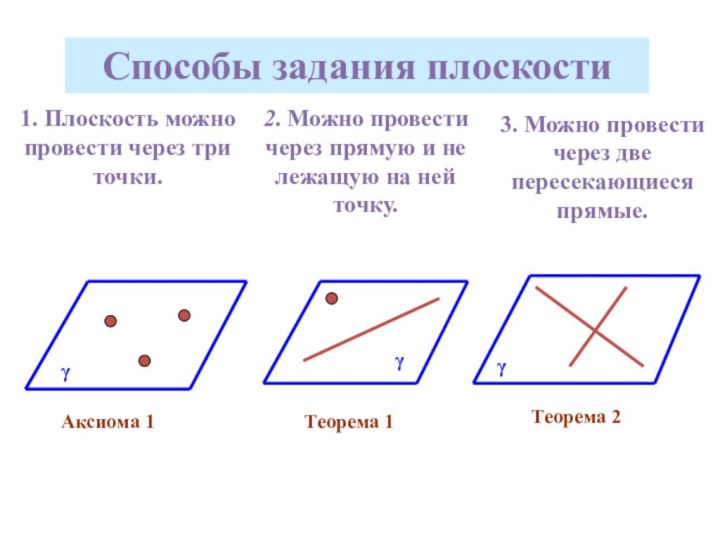
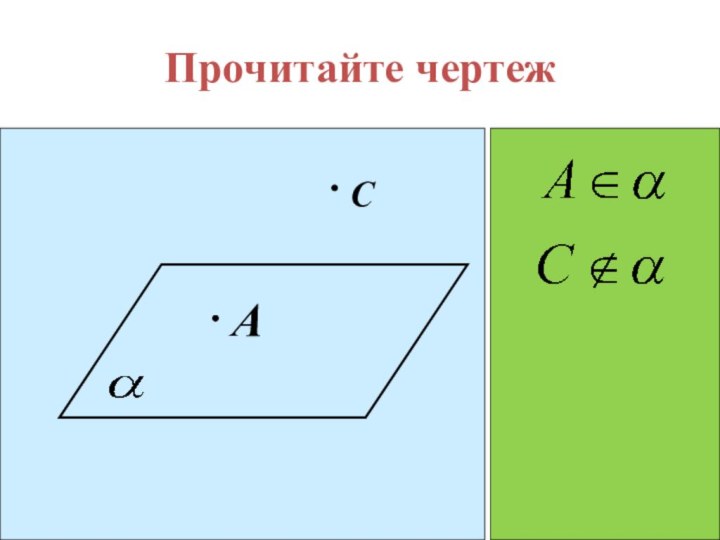
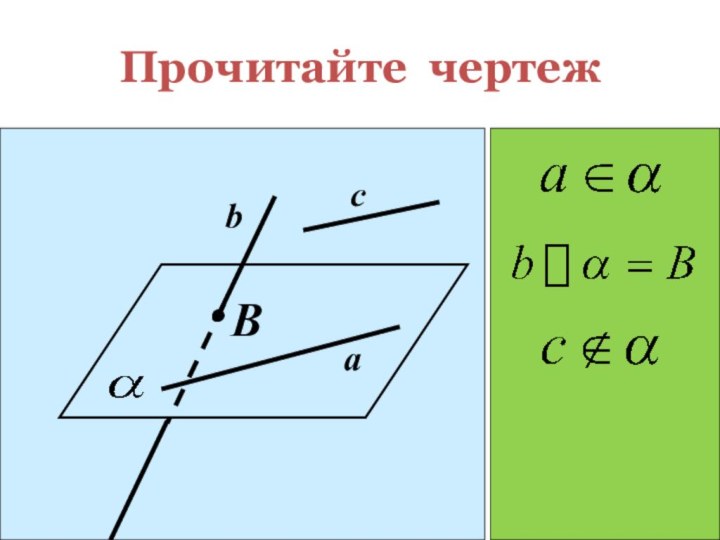
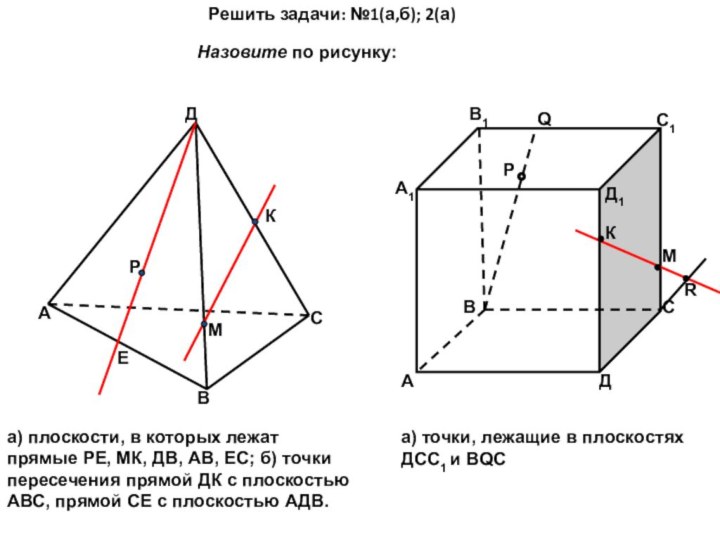
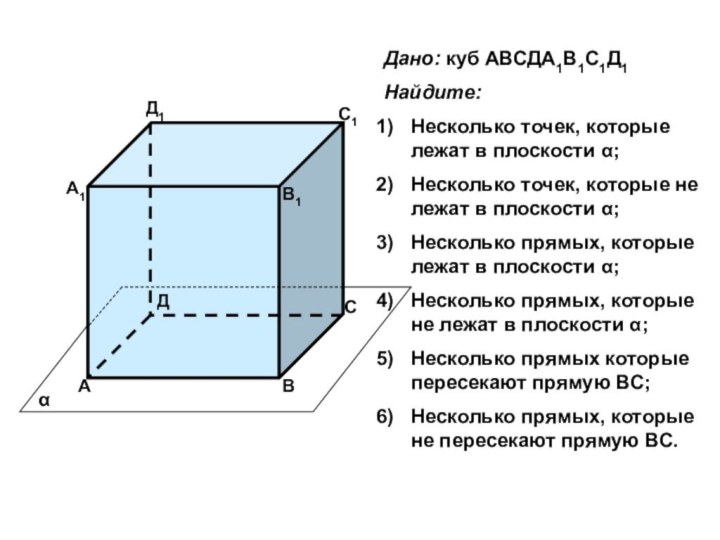
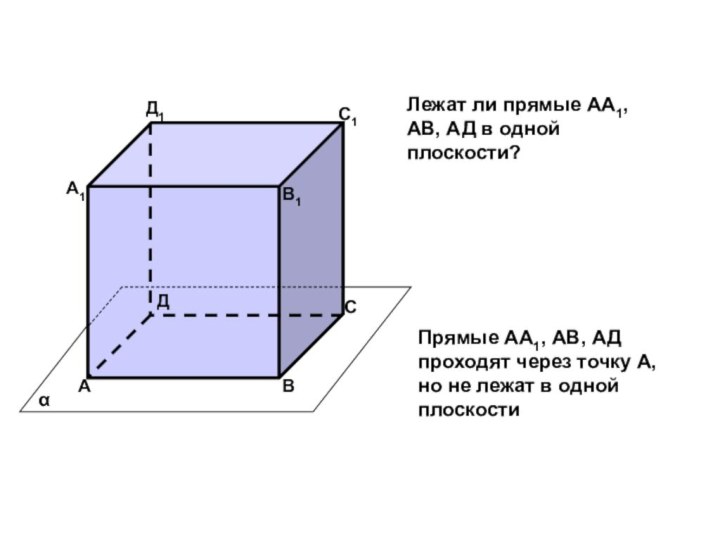
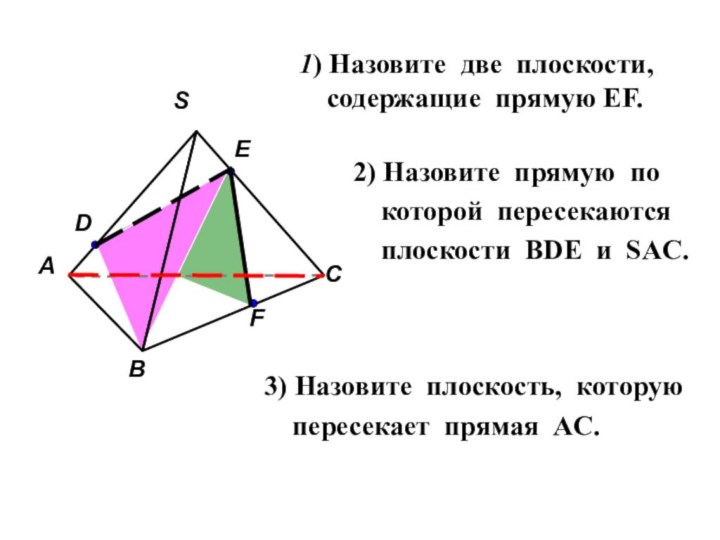
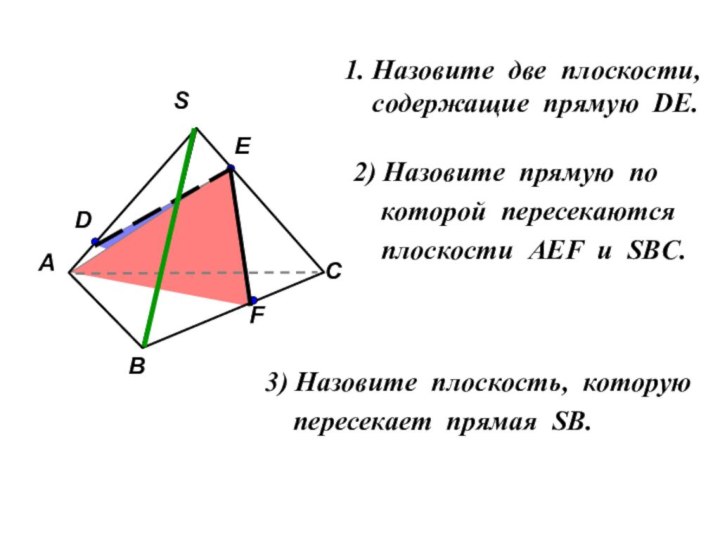
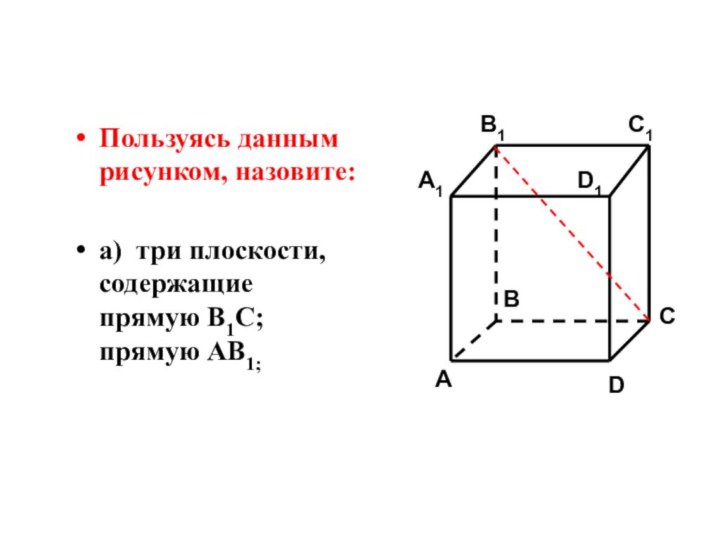
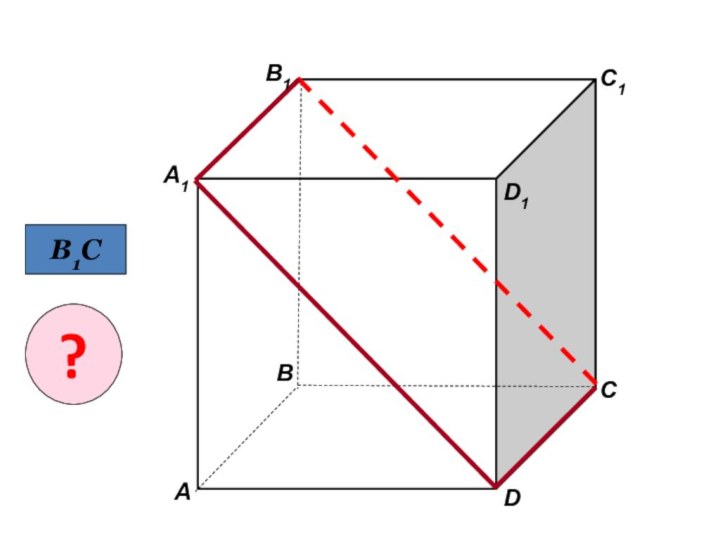
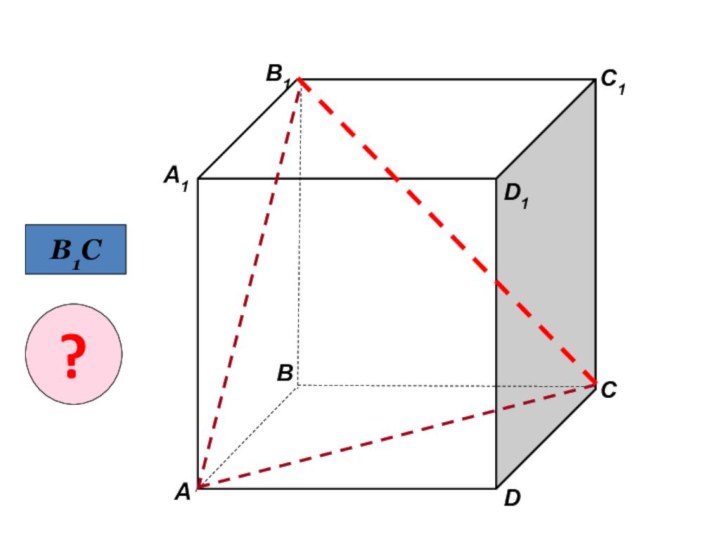
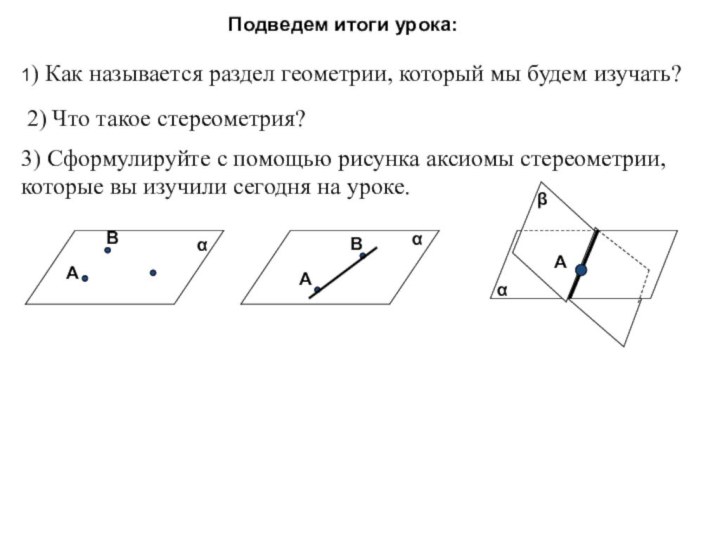
помощи доказательства
Аксиома
Положение, принимаемое без логического доказательства в силу непосредственной
убедительности; истинное исходное положение теории. Геометрия
Наука о свойствах геометрических фигур
Планиметрия
Раздел геометрии, в котором изучаются свойства фигур на плоскости.