Слайд 2
Введение
n
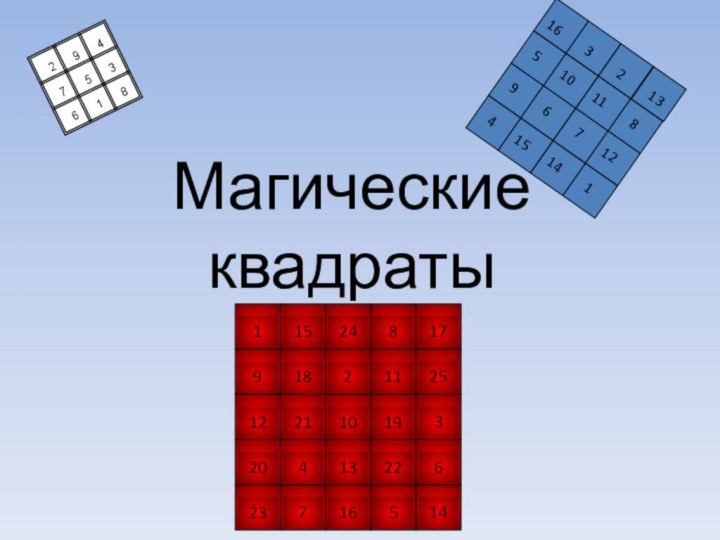
Понятие магического квадрата
Магическим «n2 - квадратом»
назовём квадрат, разделённый на n2- клеток, заполненный первыми n
натуральными числами так, что суммы чисел, стоящих в любом горизонтальном или вертикальном ряду, а также на любой из диагоналей квадрата, равны одному и тому же числу
Sn=
Слайд 4
Квадрат третьего порядка
Квадрат третьего порядка существует лишь один,
если не считать квадратов созданных путем перестановок данного.
Сумма чисел,
стоящих в любой строке, в любом столбце и на каждой из главных диагоналей равна 15
Слайд 5
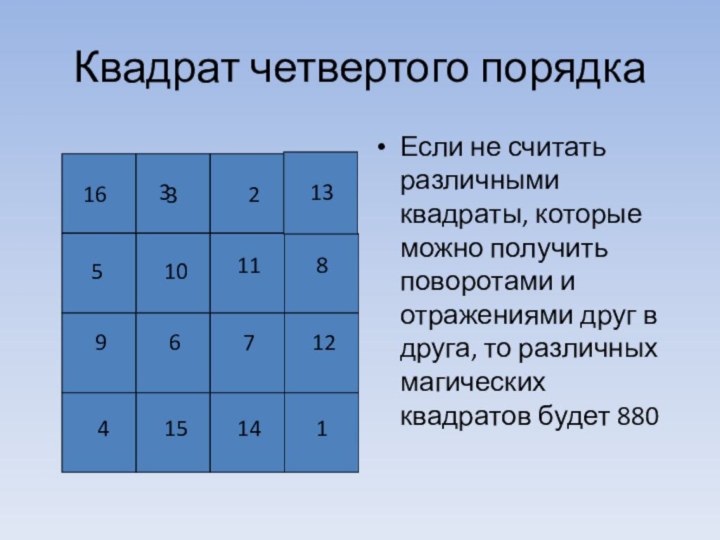
Квадрат четвертого порядка
Если не считать различными квадраты, которые
можно получить поворотами и отражениями друг в друга, то
различных магических квадратов будет 880
Слайд 6
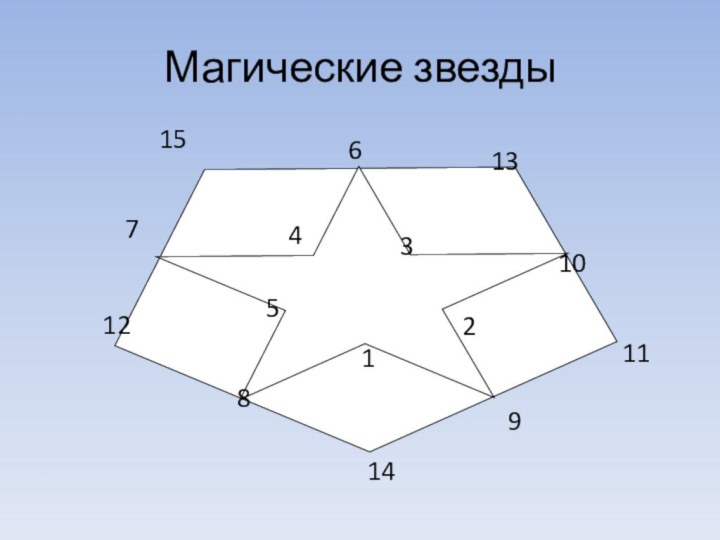
Другие магические фигуры
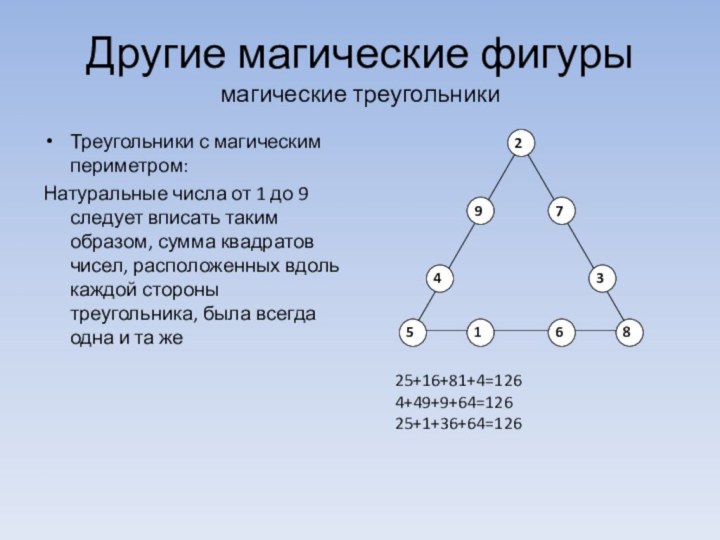
магические треугольники
Треугольники с магическим периметром:
Натуральные
числа от 1 до 9 следует вписать таким образом,
сумма квадратов чисел, расположенных вдоль каждой стороны треугольника, была всегда одна и та же
25+16+81+4=126
4+49+9+64=126
25+1+36+64=126
Слайд 7
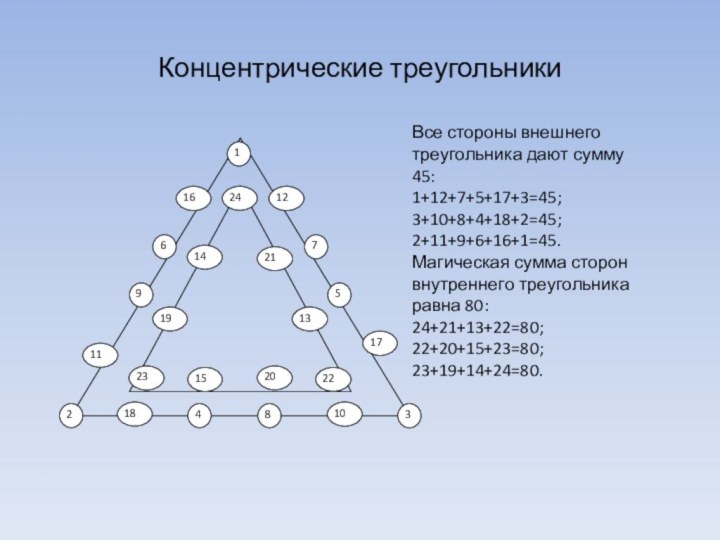
Концентрические треугольники
Все стороны внешнего треугольника дают сумму 45:
1+12+7+5+17+3=45;
3+10+8+4+18+2=45;
2+11+9+6+16+1=45.
Магическая
сумма сторон внутреннего треугольника равна 80:
24+21+13+22=80;
22+20+15+23=80;
23+19+14+24=80.
Слайд 9
Исследовательская работа
Целью данной работы является определение "магических" объемных
фигур - "магических" многогранников. "Магическим" назовем многогранник, у которого
числа, расположенные на гранях, имеющие общую вершину, составляют "постоянную" сумму, причем числа не повторяются.
Для достижения данной цели поставим следующие задачи:
Найти "магические" многогранники среди правильных объемных фигур - тетраэдра, куба, октаэдра, додекаэдра, икосаэдра;
Найти "магические" многогранники среди произвольных объемных фигур.
Слайд 10
Решение задач исследования
Тетраэдр
a
b
c
Тетраэдр имеет четыре грани и четыре
вершины, значит требуется расставить четыре числа. Поместим числа а,
b, с на гранях, имеющие общую вершину С, их сумма S при данной вершине равна а + b+ с, т. е. такая же сумма должна быть и при вершине В. Для выполнения этого условия необходимо, чтобы на оставшейся четвертой грани находилось число с. Это противоречит определению "магического" многогранника, следовательно, тетраэдр не может являться этой фигурой.
Слайд 11
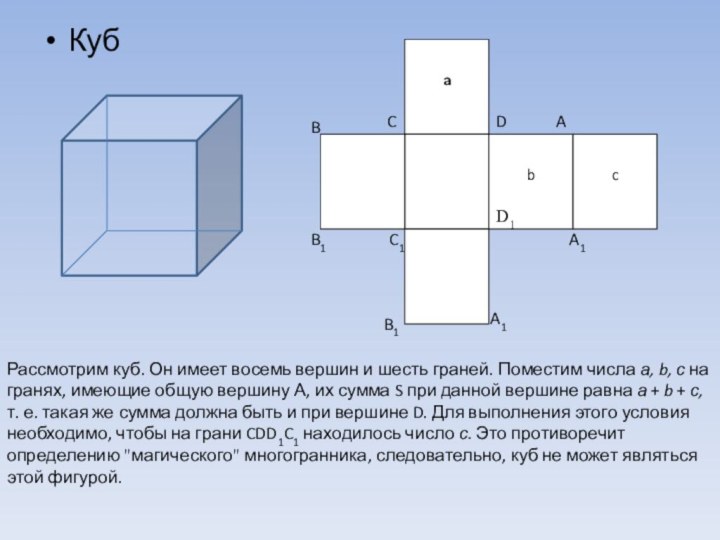
Куб
Рассмотрим куб. Он имеет восемь вершин и
шесть граней. Поместим числа а, b, с на гранях,
имеющие общую вершину А, их сумма S при данной вершине равна а + b + с, т. е. такая же сумма должна быть и при вершине D. Для выполнения этого условия необходимо, чтобы на грани CDD1C1 находилось число с. Это противоречит определению "магического" многогранника, следовательно, куб не может являться этой фигурой.
Слайд 12
Октаэдр
Перейдем теперь к октаэдру . Он имеет
восемь граней и шесть вершин. Будем расставлять восемь последовательных
чисел: а, а + 1, а + 2, а + 3, а + 4, а + 5, а + 6, а + 7. Найдем сумму при вершине: S=(a+a+1+a+2+a+3+a+4+a+5+a+6+a+7)/2=4a+14. Так как у октаэдра шесть вершин, то требуется представить эту сумму данными числами шестью разными вариантами. Получаем:
4а + 14 = а + а + 3 + a+ 4 + а + 7;
4а + 14 = а + а + 3 + а + 5 + а + 6;
4а + 14 = а + 1 + а + 2 + а + 5 + а + 6;
4а + 14 = а + 1 + а + 2 + а + 4 + а + 7;
4а + 14 = а + а + 1 + а + 6 + а + 7;
4а + 14 = а + 2 + а + 3 + а + 4 + а + 5;
Следовательно, сумма при любой из шести вершин будет равна одному и тому же числу. Значит, октаэдр является "магической" фигурой.
Слайд 13
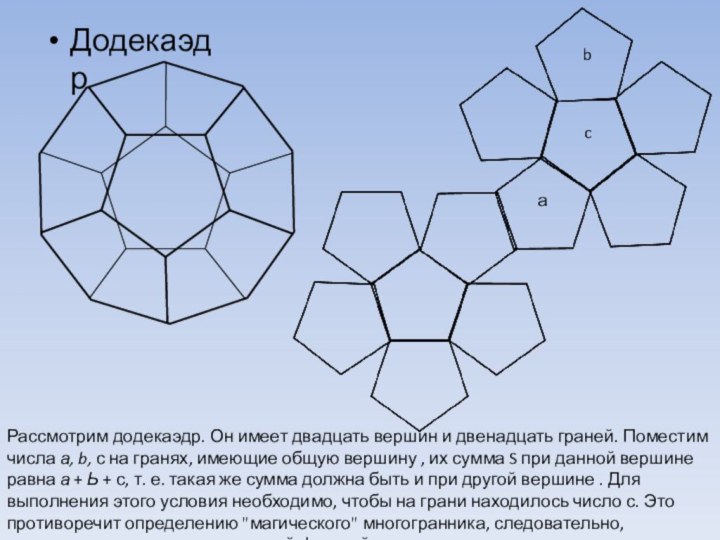
Додекаэдр
Рассмотрим додекаэдр. Он имеет двадцать вершин и
двенадцать граней. Поместим числа а, b, с на гранях,
имеющие общую вершину , их сумма S при данной вершине равна а + Ь + с, т. е. такая же сумма должна быть и при другой вершине . Для выполнения этого условия необходимо, чтобы на грани находилось число с. Это противоречит определению "магического" многогранника, следовательно, додекаэдр не может являться этой фигурой.
Слайд 14
Икосаэдр
Перейдем к рассмотрению икосаэдра. Он имеет двадцать
граней и двенадцать вершин. Будем расставлять двадцать последовательных чисел:
a,a+1,a+2 . . . a+19. Найдем сумму при вершине: S=( a+a+1+a+2+. . .+ a+19)/4=(20a + 190)/4=5a+47,5. Но сумма должна быть целым числом.
Слайд 15
Поиск других “магических” многогранников
Разделим каждую грань куба на
16 равных квадратиков и поместим в них числа от
1 до 96 таким образом, что с любой стороны любой ряд чисел, - слева направо, сверху вниз, по большим диагоналям, - в сумме дает 194. Учтем, что не одно число не будет повторяться в этих квадратиках.