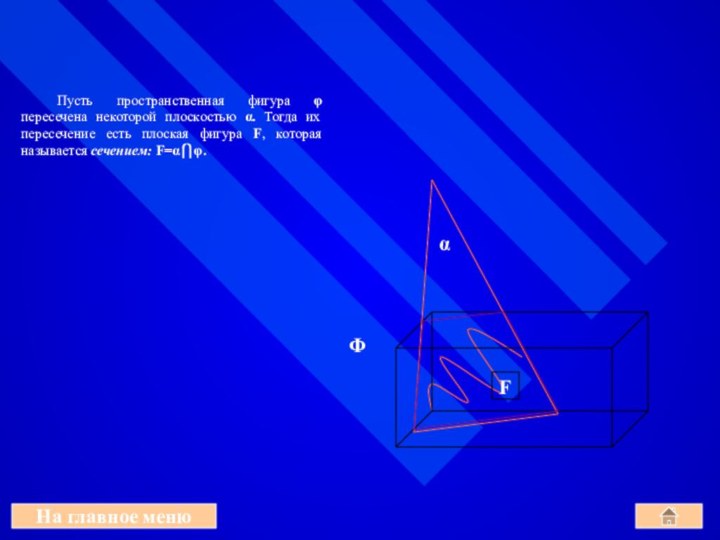
аксиомы геометрии
Сечения многогранников
Тела вращения и их сечения
Об авторе
Список используемой
и рекомендуемой литературы
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Email: Нажмите что бы посмотреть








































1 Лазарев Л. Инженеры завтрашнего дня. “Известия” от 13 марта 1963 г.
На главное меню
На главное меню
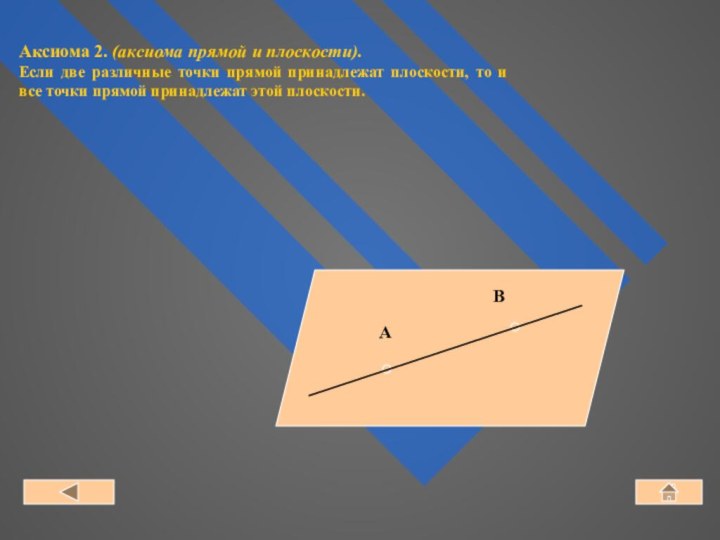
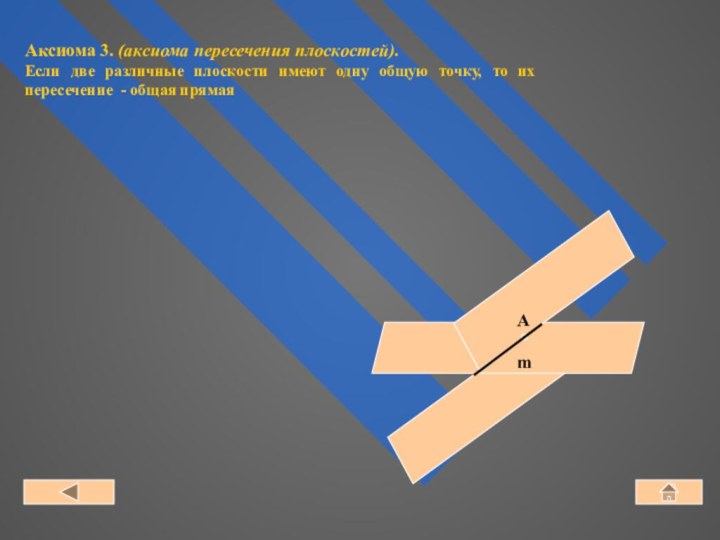
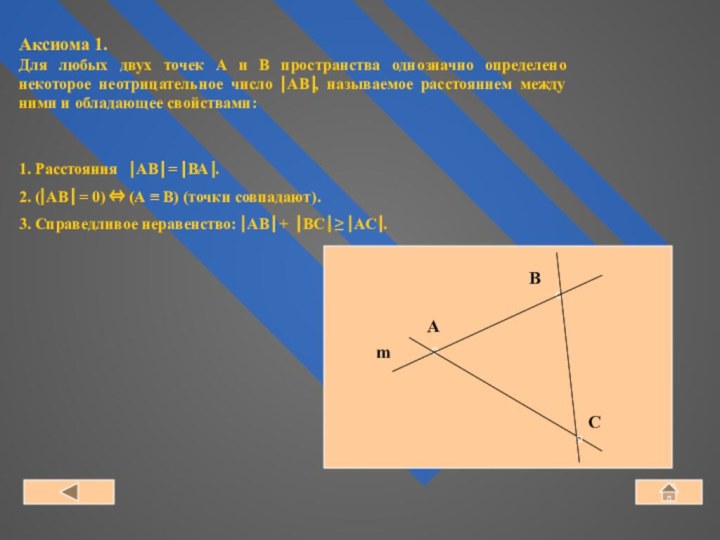
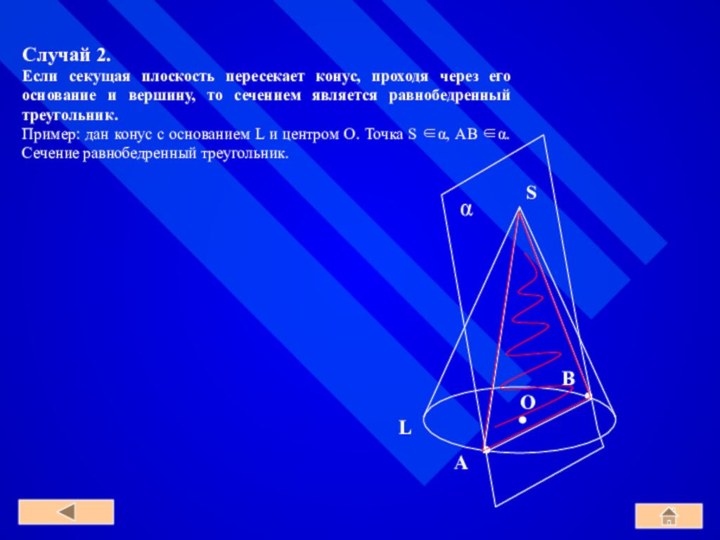
1. Расстояния ⎢АВ⎟ = ⎢ВА⎟.
2. (⎢АВ⎟ = 0) ⇔ (А ≡ В) (точки совпадают).
3. Справедливое неравенство: ⎢АВ⎟ + ⎢ВС⎟ ≥ ⎢АС⎟.
Переход к следующему шагу задачи производится при нажатии левой клавиши мыши или Пробела
Решение:
1. т.к. Q є BCC1, R є BCC1, то
RQ є BCC1. Проведем ее.
Это след плоскости PQR на BCC1.
2. Прямая QR∩BB1=B2, QR∩CC1.
Это следы PQR на прямых BB1 и CC1.
3. т.к. B2 є ABB1 и P є ABB1,
B2P є ABB1. B2P – след плоскости
PQR на ABB1A1.
4. т.к. C2 є AСС1 и P є AСС1, то
С2P є AСС1. Проведем ее. PC2∩A1C1=V.
Это след плоскости PQR на ACC1.
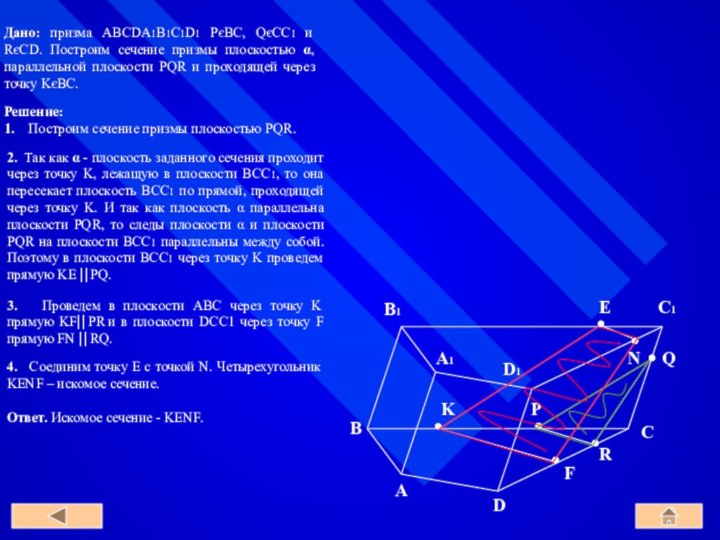
Дано: призма ABCA1B1C1,
P є AA1, Q є B1C1, R є BCC1B1.
Построим сечение призмы
плоскостью PQR.
6. Итак, B2QVP – это искомое сечение.
Ответ. Искомое сечение B2QVP.
Решение:
1. Отрезок PR – это след плоскости PQR на грани АВВ1А1.
2. Примем плоскость АВС за основную. Построим проекции на ABC точек P, Q и R (в направлении, параллельном боковому ребру призмы). Получаем точку P′, R′, Q′.
3. Параллельными прямыми PP′ и QQ′ определяется плоскость β1. Строим сечение призмы плоскостью β1. Это – первое вспомогательное сечение.
4. Параллельными прямыми RR′ и DD′ определяется плоскость β2. Строим сечение призмы плоскостью β2. Это – второе вспомогательное сечение.
5. Строим линию пересечения плоскостей β1 и β2. F=P′Q′⎧⎫AD и точка F1=В1Q⎧⎫А1D1. Это прямая FF1. Строим.
7. Проведем прямую RF2 и находим точку D2=RF2⎧⎫DD1. Так как точка D2 є RF2, то D2 є PQR. D2 – это след плоскости PQR на прямой DD1.
8. Проводим прямую D2Q. Это след плоскости PQR на DEE1. На прямой EE1 получаем т. E2=RF2⎧⎫ЕЕ1. Отрезок QE2 – это след плоскости PQR на грани DЕЕ1D1.
9. Проводим прямую RE2. Отрезок RE2 – это след плоскости PQR на грани АЕЕ1А1.
10. RR′ || СС1. Ими определяется плоскость β3. Строим сечение призмы плоскостью β3. Это – третье вспомогательное сечение.
11. Находим линию пересечения плоскостей β1 и β3. Это прямая КК1, где К=R′С⎧⎫P′Q′ и точка К1=А1С1⎧⎫B1Q. Находим точку К2= PQ⎧⎫КК1. Проводим RК2. С2=RК2⎧⎫СС1.
12. Проводим прямые PC2 и C2D2. Получаем отрезки PC2, C2L и LQ – следы плоскости PQR соответственно на гранях ВСС1В1, CDD1C1 и A1B1C1D1E1.
6. В плоскости β1 проводим прямую PQ. Строим F2=PQ⎧⎫FF1. Так как F2 є PQ, то F2 є PQR. Тогда прямая RF2 є PQR.
13. Итак, совокупность построенных следов плоскости PQR на гранях призмы образует многоугольник PRE2QLC2, который и является искомым сечением.
Ответ. PRE2QLC2 – искомое сечение.
Решение:
1. Построим сечение призмы плоскостью PQR.
2. Так как α - плоскость заданного сечения проходит через точку K, лежащую в плоскости BCC1, то она пересекает плоскость BCC1 по прямой, проходящей через точку K. И так как плоскость α параллельна плоскости PQR, то следы плоскости α и плоскости PQR на плоскости BCC1 параллельны между собой. Поэтому в плоскости BCC1 через точку K проведем прямую KE ⎜⎜PQ.
3. Проведем в плоскости ABC через точку K прямую KF⎜⎜PR и в плоскости DCC1 через точку F прямую FN ⎜⎜RQ.
4. Соединим точку E с точкой N. Четырехугольник KENF – искомое сечение.
Ответ. Искомое сечение - KENF.
Решение:
1. Плоскость, проходящая через прямую AR и т. Q есть MAB. В плоскости MAB через т. Q проведем прямую QF ⎜⎜AR.
2. Пересекающимися прямыми PQ и QF определяется плоскость α ( PQF) - плоскость искомого сечения.
3. Построим проекции точек F и Q на плоскости ABC (в направлении параллельном ребрам). Это т.F'≡B и т.Q'≡A. Тогда точка S1=FQ⎧⎫F′Q′ лежат на основном следе секущей плоскости α.
4. Так как точка P лежит на основном следе секущей плоскости α, то прямая S1P – след плоскости α, а отрезок S2P – след плоскости α на грани ABC. Далее ясно, что точку P следует соединить с точкой F. В итоге четырехугольник PFQS2 – искомое сечение.
Ответ. Искомое сечение PFQS2.
Решение:
1. В плоскости ABC через точку Q проведем прямую, параллельную прямой CD, и найдем точки S1, S2 и S3, в которых эта прямая пересекает соответственно прямые BC, AD и AB.
2. Пересекающимися прямыми PQ и S1S2 определяется плоскость β - плоскость вспомогательного сечения. Построим это сечение.
Основным следом плоскости β является прямая S1S2. Отрезок PS1– след плоскости β на грани MBC, прямая PS3 – ее след на плоскости MAB, отрезок PA1 – на грани MAB, отрезок A1S2 – на грани MAD.
3. Строим далее сечение пирамиды плоскостью α, проходящей через точку K параллельно плоскости β. В итоге получаем многоугольник KB1C1D1 – искомое сечение.
Ответ. KB1C1D1 – искомое сечение.
β
3. Точка F является общей точкой плоскостей PQR и MDB, т.е. эти плоскости пересекаются по прямой, проходящей через точку F. Вместе с тем так как PQ – средняя линия треугольника ABD, то PQ⎜⎜BD, т.е. прямая PQ параллельна и плоскости MDB. Тогда плоскость PQR, проходящая через прямую PQ, пересекает плоскость MDB по прямой, параллельной прямой PQ, т.е. параллельной и прямой BD. Поэтому в плоскости MDB через точку F проведем прямую, параллельную прямой BD.
Решение:
1. Основным следом плоскости PQR является прямая PQ. Найдем точку K, в которой плоскость MAC пересекает прямую PQ. Точки K и R принадлежат и плоскости PQR, и плоскости MAC. Поэтому, проведя прямую KR, мы получим линию пересечения этих плоскостей.
2. Найдем точку N=AC⎧⎫BD, проведем прямую MN и найдем точку F=KR⎧⎫MN.
4. В итоге получаем многоугольник PQD1RB1 искомое сечение.
Ответ. PQD1RB1- искомое сечение.
1. Если через какую-нибудь точку прямой BC1 провести две прямые, перпендикулярные прямой BC1, то этими пересекающимися прямыми определится плоскость, перпендикулярная прямой BC1.Проведем построение.
2. Так как четырехугольник BCC1B1 является квадратом, то B1C ⊥ BC1.Проведя прямую B1C, мы получим первую прямую перпендикулярную прямой BC1.
4. Зная это отношение, построим точку H и проводим прямую PH, которая и является прямой, перпендикулярной BC1. Затем в плоскости BCC1B1 через точку H проведем прямую, параллельную прямой B1C. Пусть эта прямая пересекает прямые BB1 и BC соответственно в точках B2 и S1. Таким образом, прямая B2S1 перпендикулярна прямой BC1. Пересекающимися прямыми PH и B2S1 определяется плоскость β - плоскость искомого сечения.
5. Построим сечение призмы плоскостью β. Получаем последовательно: точку S2= PS1⎧⎫AB, прямую B2S2, точку A2= B2S2⎧⎫AA1 и, наконец, четырехугольник PA2B2S1 – искомое сечение.
Ответ. PA2B2S1 – искомое сечение.
На главное меню
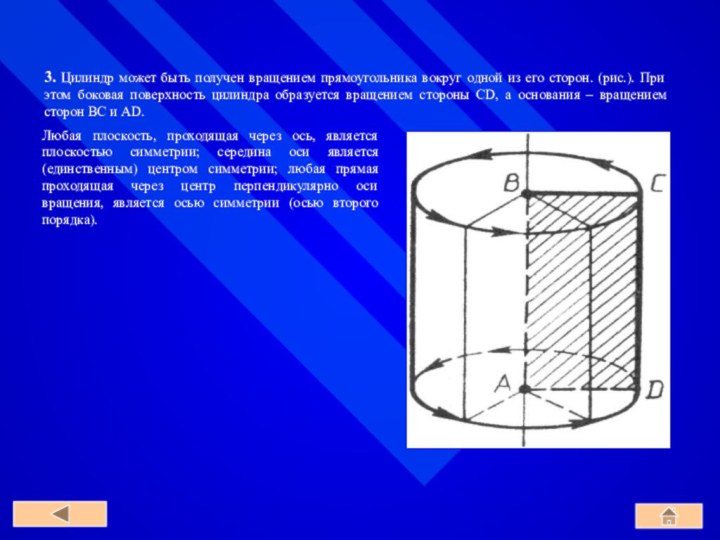
Рис.
На главное меню
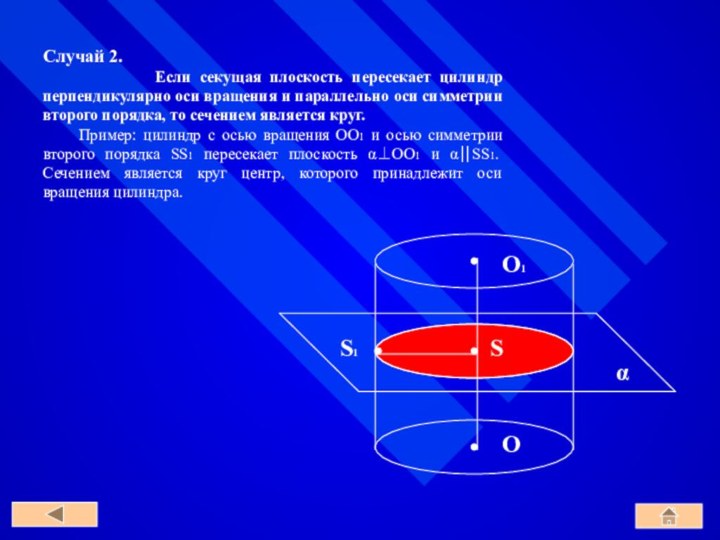
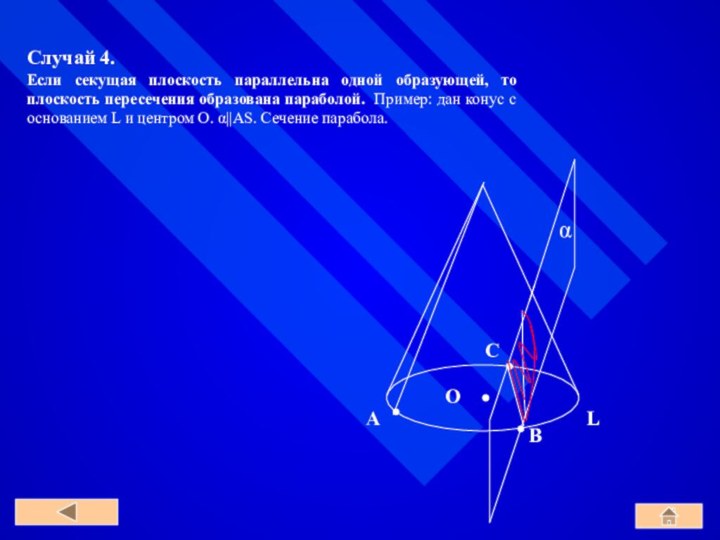
По построению концы образующих, расположенные в плоскости α, заполняют окружность L. Концы же образующих, расположенные в плоскости β, заполняют окружность L1 с центром O1 радиуса r, где O1 – точка пересечения плоскости β с прямой, проходящей через точку O перпендикулярно к плоскости α.
Справедливость этого утверждения следует из того, что множество концов образующих, лежащих в плоскости β, получается из окружности L параллельным переносом на вектор OO1. Параллельный перенос является движением и, значит, наложением, а при наложении любая фигура переходит в равную ей фигуру. Следовательно, при параллельном переносе на вектор OO1 окружность L переходит в равную ей окружность L1 с центром O1 радиуса r.
Любая плоскость, проходящая через ось, является плоскостью симметрии; середина оси является (единственным) центром симметрии; любая прямая проходящая через центр перпендикулярно оси вращения, является осью симметрии (осью второго порядка).
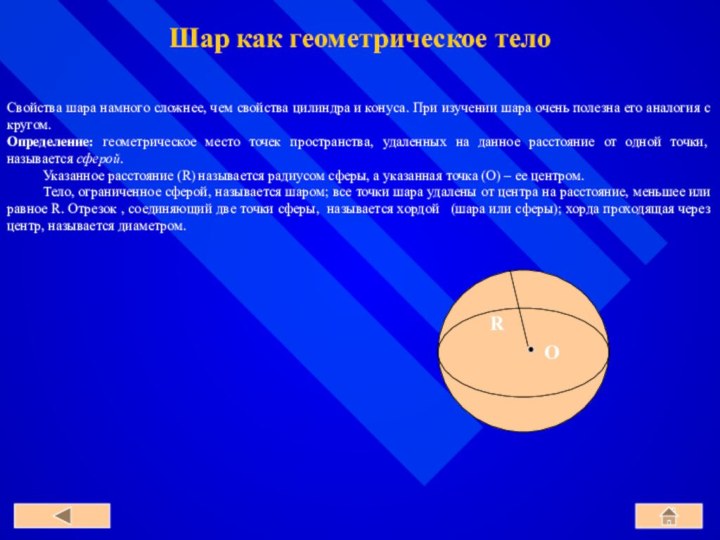
O
R