Презентация на тему по геометрии на тему: Аксиомы стереометрии (10 класс)

от греческих слов «стереос» объемный, пространственный, «метрео» – мерить.

Основные фигуры: точка, прямая, плоскость.

тела и их поверхности. Такие, как: куб, параллелепипед, призма,

пирамида.
А также тела вращения: шар, сфера, цилиндр, конус.

прописные латинские буквы:

Прямую обозначают одной строчной латинской буквой и

двумя прописными латинскими буквами:

на рисунках чаще всего плоскость изображают в виде параллелограмма.

Но следует понимать и представлять себе данную геометрическую фигуру как неограниченную во все стороны.

их плоскими изображениями на чертеже.
Изображением пространственной фигуры служит

ее проекция на плоскость.

Изображения конуса

получаем представление о геометрических свойствах реальных предметов (их форме,

взаимном расположении и т. д.) и можем использовать эти свойства в практической деятельности. В этом состоит прикладное значение геометрии.

Геометрия, в частности стереометрия, широко используется в строительном деле, архитектуре, машиностроении, геодезии, во многих
других областях науки и техники.

аксиомах. Существует множество аксиом стереометрии, в учебнике вам представлены

три:

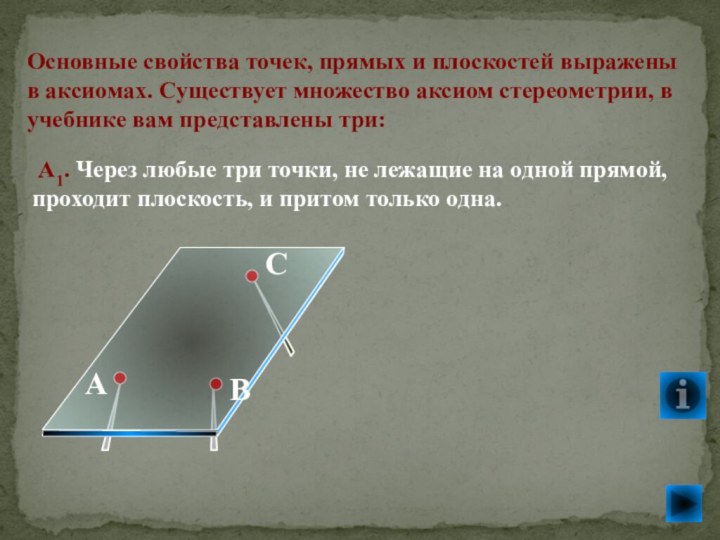
А1. Через любые три точки, не лежащие на одной прямой, проходит плоскость, и притом только одна.

A

B

C

жизни:
Табурет с тремя ножками всегда идеально встанет на пол

и не будет качаться. У табурета с четырьмя ножками бывают проблемы с устойчивостью, если ножки стула не одинаковые по длине.

Табурет качается, т. е. опирается на три ножки, а четвертая ножка (четвертая «точка») не лежит в плоскости
пола, а висит в воздухе.

то все точки прямой лежат в этой плоскости.

A
B

«ровности» чертежной линейки.

Линейку прикладывают краем к плоской поверхности

стола. Если край линейки ровный, то он всеми своими точками прилегает к поверхности стола.

Если край неровный, то в каких-то местах между ним и поверхностью стола образуется просвет.

в данной плоскости, то она имеет с ней не

более одной общей точки.
Если прямая и плоскость имеют только одну общую точку, то говорят, что они пересекаются.

они имеют общую прямую, на которой лежат все общие

точки этих плоскостей.

Самый простой пример к аксиоме А3 из повседневной жизни является пересечение двух смежных стен комнаты.

и не лежащую на ней точку проходит плоскость, и

притом только одна.

М

a

плоскость, и притом только одна
М

a
b


N

прямые
РЕ, МК, DB, AB, EC

Назовите точки пересечения прямой DK

с плоскостью АВС

Назовите точки, лежащие в плоскостях АDB и DBC

P

E

A

B

C

D

M

K