измерения наших умственных способностей и дает нам возможность правильно
мыслить и рассуждать.»Галилео Галилей
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Email: Нажмите что бы посмотреть








h
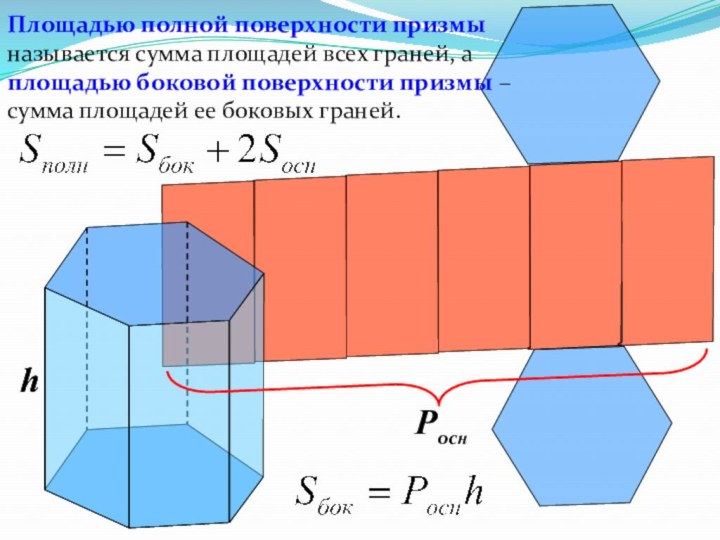
h
Pocн