Презентация на тему Прямоугольная система координат в пространстве

называются осями координат, а их общая точка – началом

координат Ох и Оу, Оу и Оz, Оz и

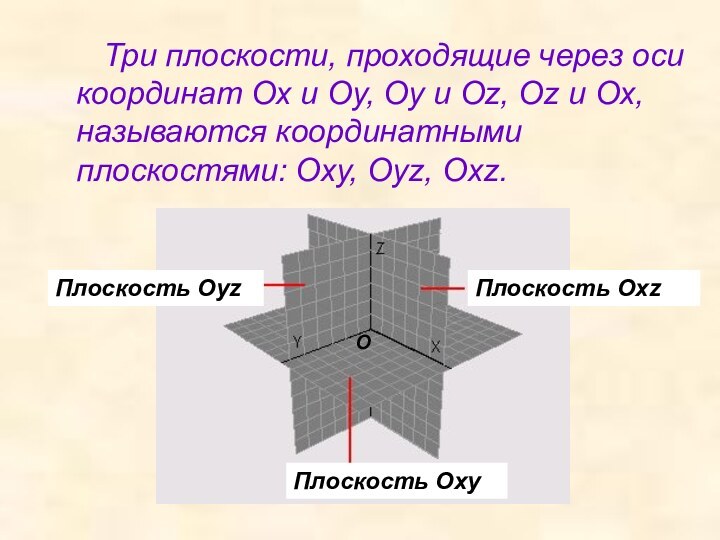
Плоскость Oxz

Плоскость Oxy

Плоскость Oyz

O

М пространства сопоставляется тройка чисел – её координаты: М

– единичный вектор оси абсцисс, j – единичный вектор

x

z

y

O

т.е. представить в виде:
Нулевой вектор можно представить в виде:
Координаты

x2; y1+ y2; z1+ z2 }.
Разность векторов: a –

Д 1(1;1;0)

прямоугольной системой координат, научились строить точку по заданным ее

{ x1; y1; z1 } и b { x2;

а {2; -4; 3} и b {-3; 1/2;

2 вариант
№1. Даны векторы а {1; -3; -1} и b {-1; 2; 0}. Найдите координаты вектора с = a – b.
№2. Даны векторы а {2; 4; -6}, b {-3; 1; 0}, c {3; 0; -1}. Найдите координаты вектора p = -1/2a + 2b – c.
№3. Найдите значения m и n, при которых векторы а {-4; m; 2} и b {2; -6; n} коллинеарны.

начало – с началом координат, называется радиус-вектором данной точки.
Координаты

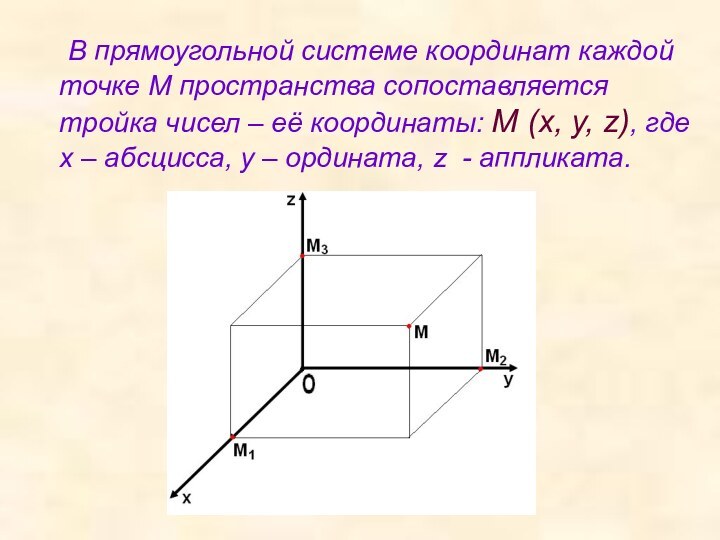
М (x; y; z)
OM (x; y; z)

A (x1; y1; z1), B (x2; y2; z2) AB (x2 – x1; y2 – y1; z2 – z1)

(x2; y2; z2), C (x; y; z)

2. Вычисление длины вектора по его координатам:
если а { x; y; z }, то

3. Расстояние между двумя точками:

b сонаправлены, то α = 0°.
Если a ||

· | b | · cos(a ^ b)
2) a

0; 0), А(0; 1; 0), D(1; 1;0), B1(0; 0;