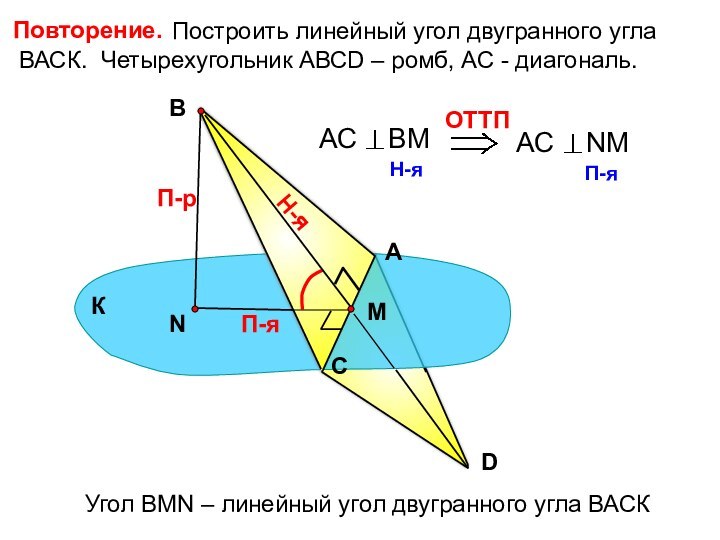
Построить линейный угол двугранного угла
ВАСК. Четырехугольник АВСD – ромб, АС - диагональ.А
С
В
П-р
Н-я
П-я
Угол ВMN – линейный угол двугранного угла ВАСК
К
D
Повторение.
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Email: Нажмите что бы посмотреть





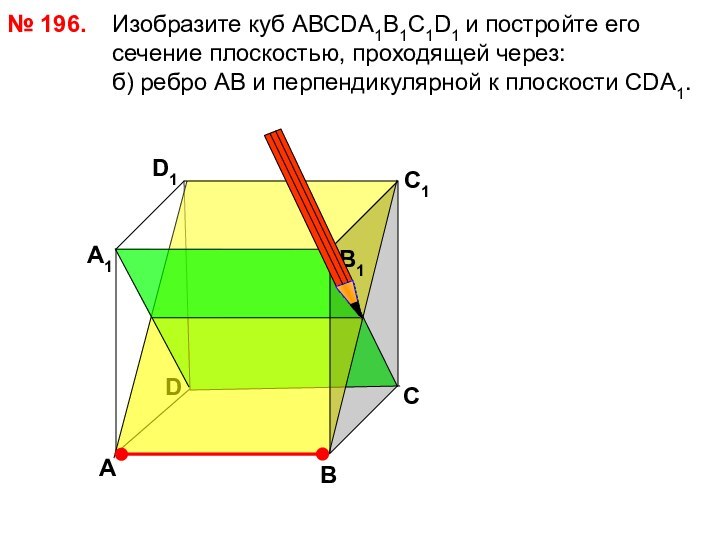
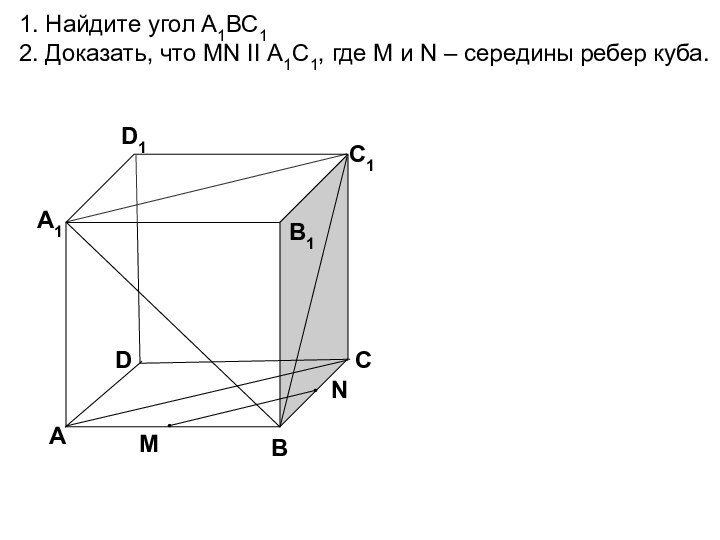
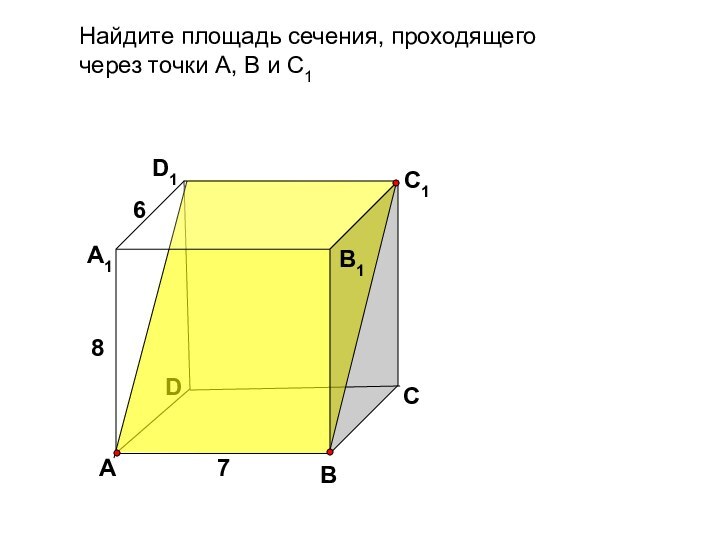
А
С
В
П-р
Н-я
П-я
Угол ВMN – линейный угол двугранного угла ВАСК
К
D
Повторение.
А
В
П-р
Н-я
П-я
Угол ВСN – линейный угол двугранного угла ВАСК
К
С
D
2
1
Повторение.
А
В
П-р
Н-я
П-я
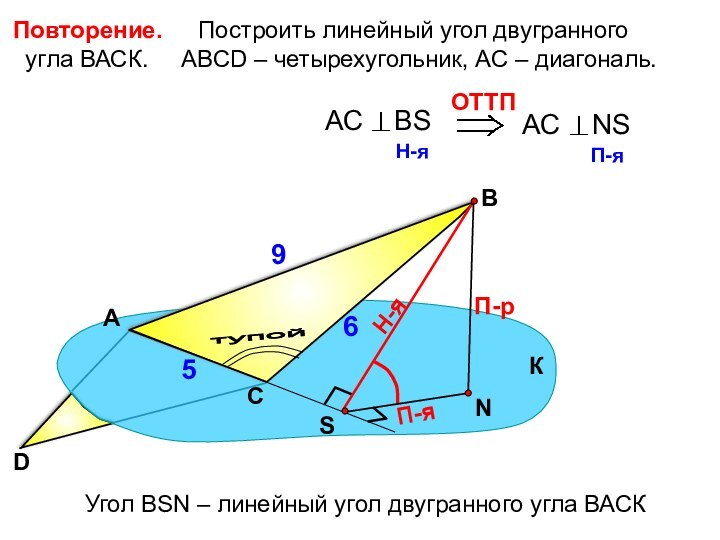
Угол ВSN – линейный угол двугранного угла ВАСК
К
С
D
9
6
5
тупой
Повторение.
А
С
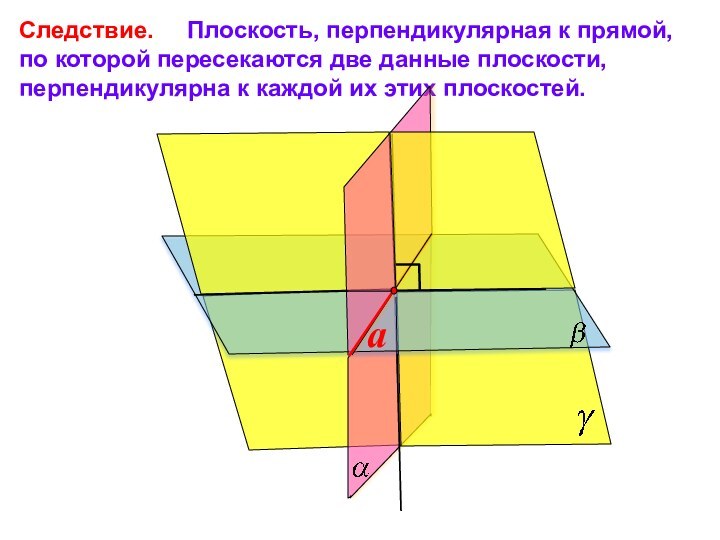
№ 178.
c
C
Подсказка
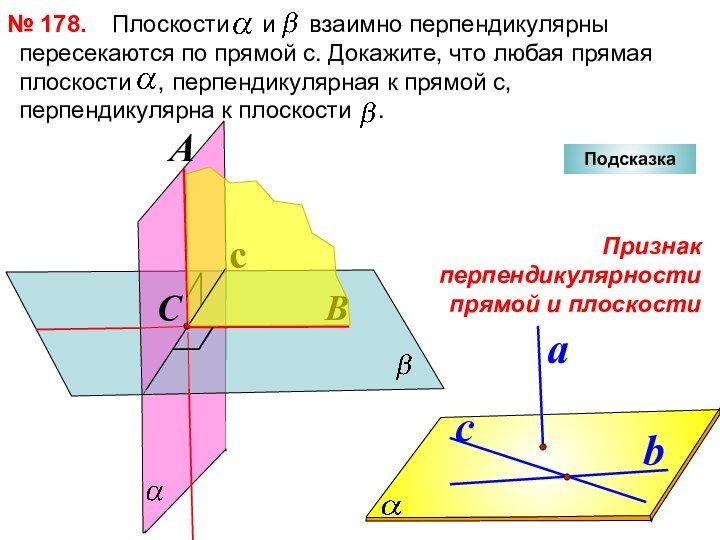
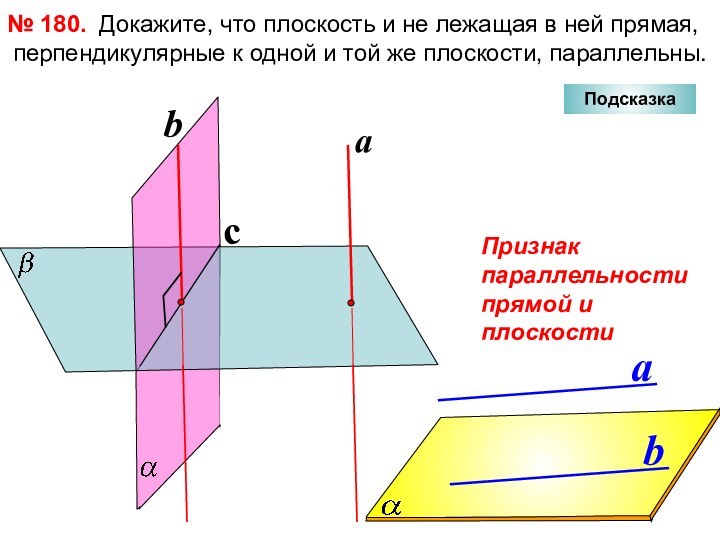
№ 180.
c
Подсказка
№ 182.
a
С
М
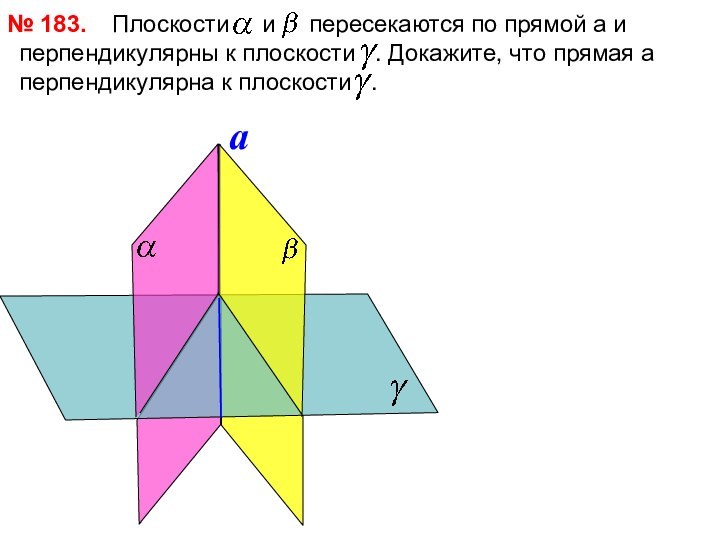
№ 183.
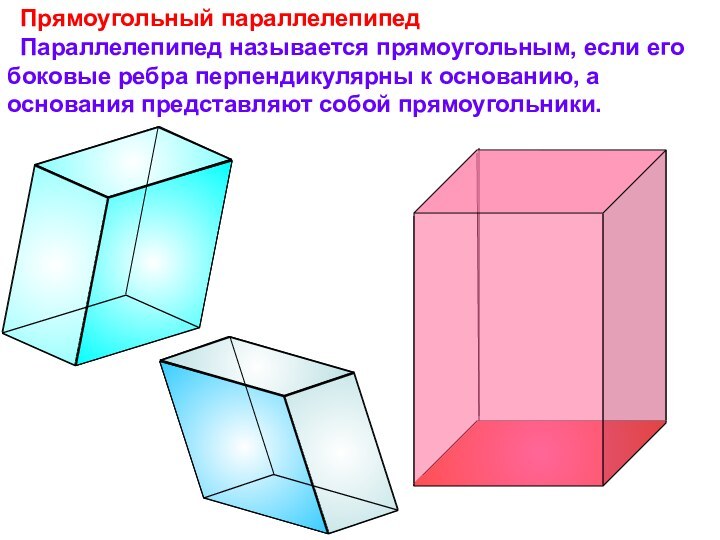
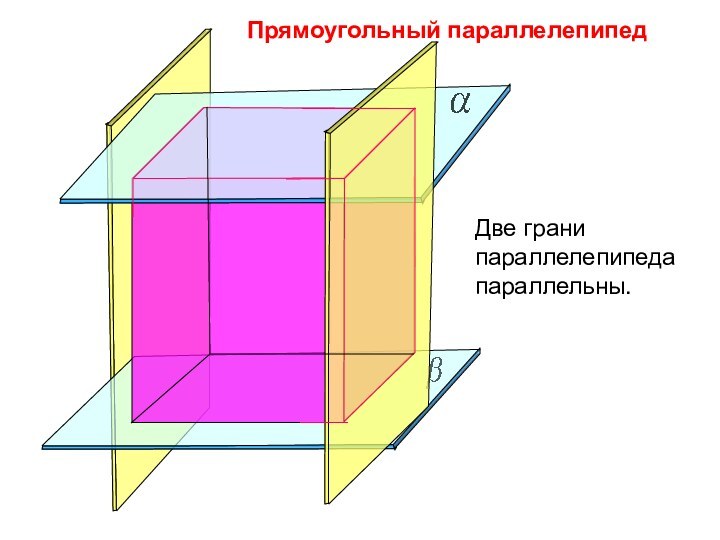
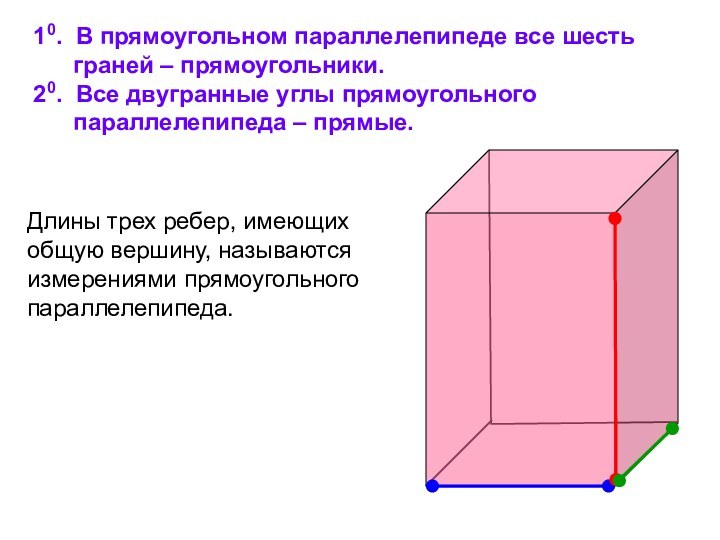
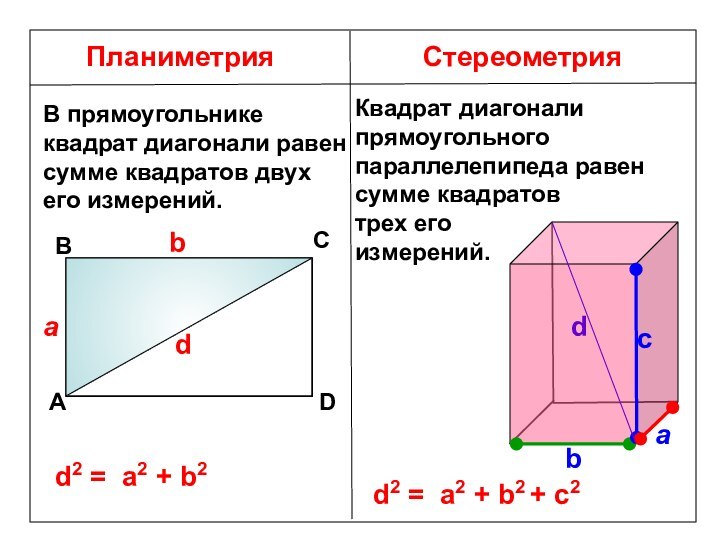
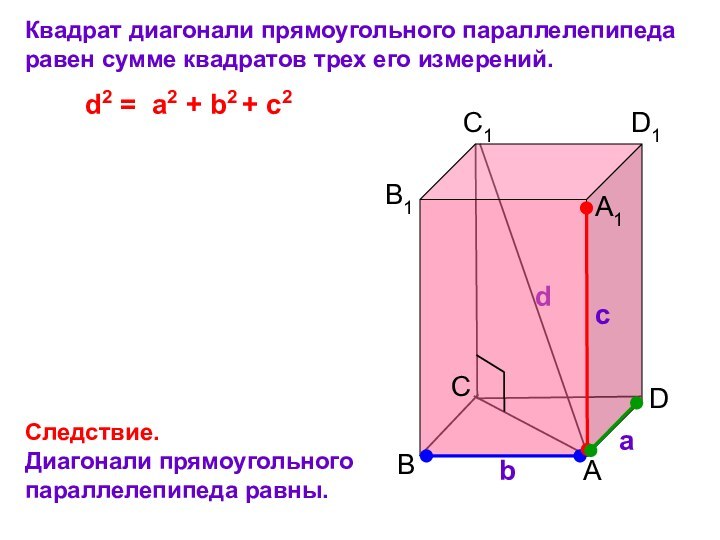
Длины трех ребер, имеющих общую вершину, называются измерениями прямоугольного параллелепипеда.
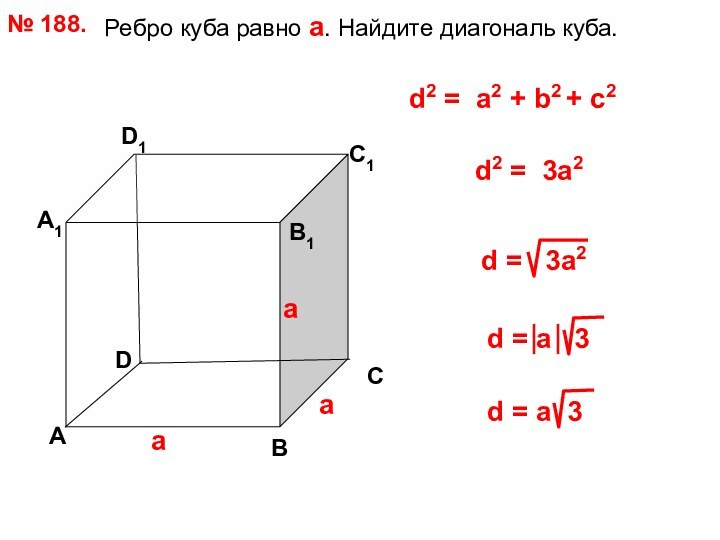
d2 = a2 + b2 + с2
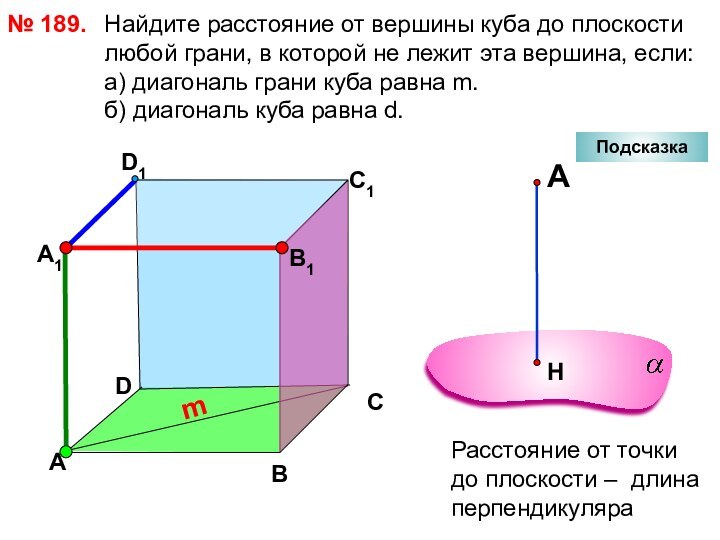
№ 189.
D
А
В
С
D1
С1
m
Подсказка
В1
А1
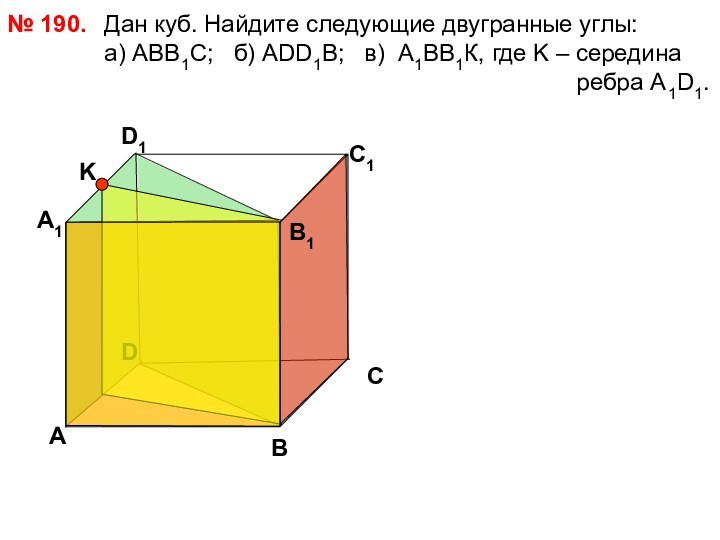
№ 190.
D
А
В
С
А1
D1
С1
В1
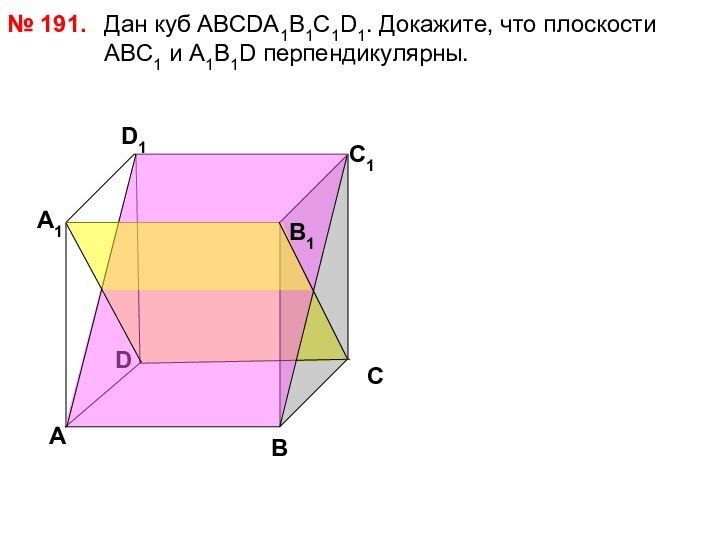
№ 191.
D
А
В
С
А1
D1
С1
В1
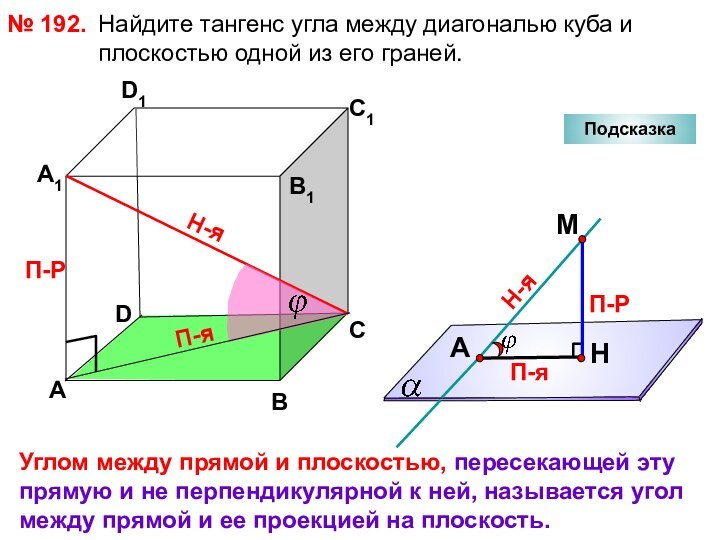
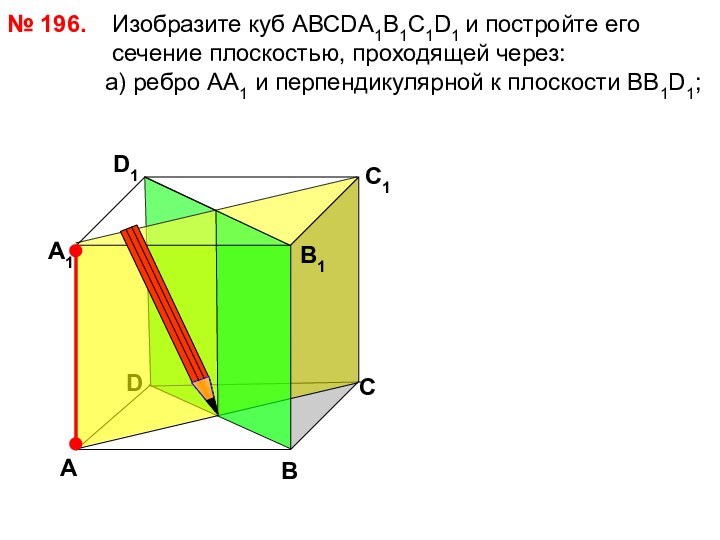
№ 192.
D
А
В
С
А1
D1
С1
В1
Подсказка
П-Р
Н-я
Подсказка
В1
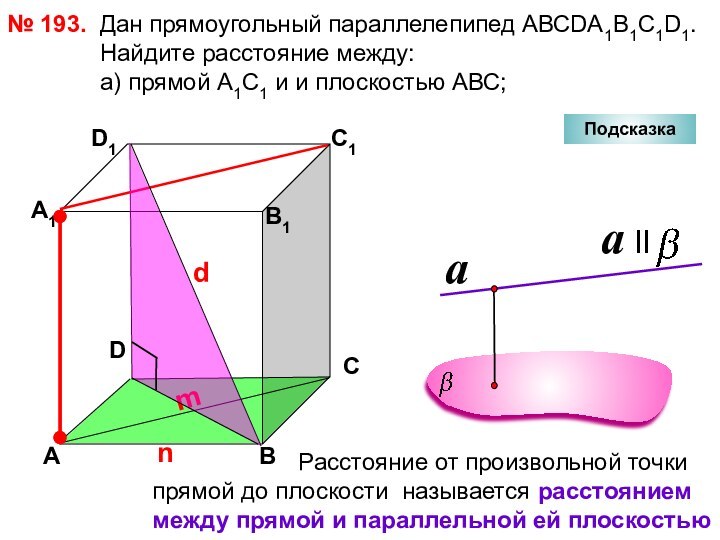
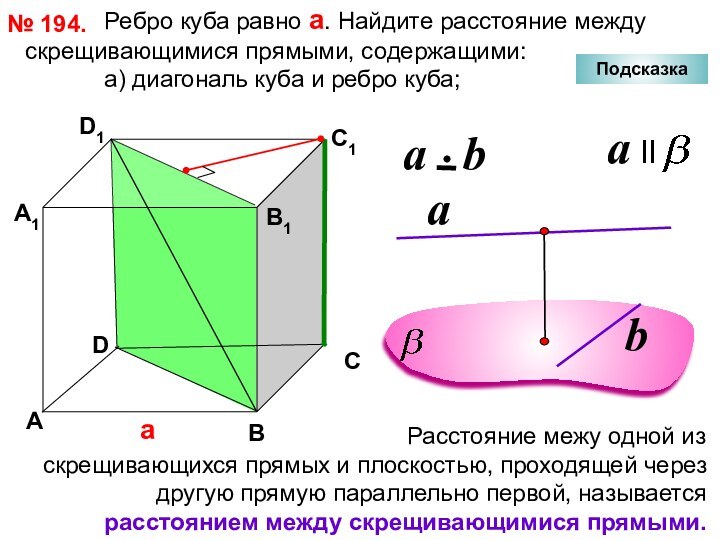
№ 194.
D
А
В
С
D1
С1
а
В1
А1
Подсказка
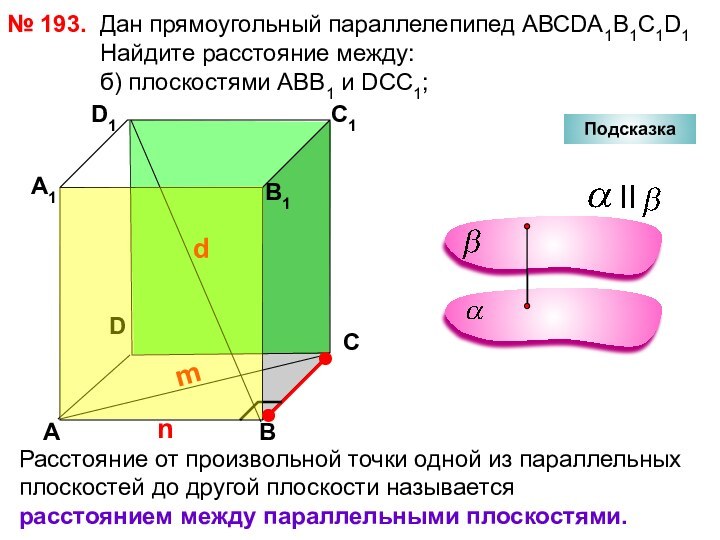
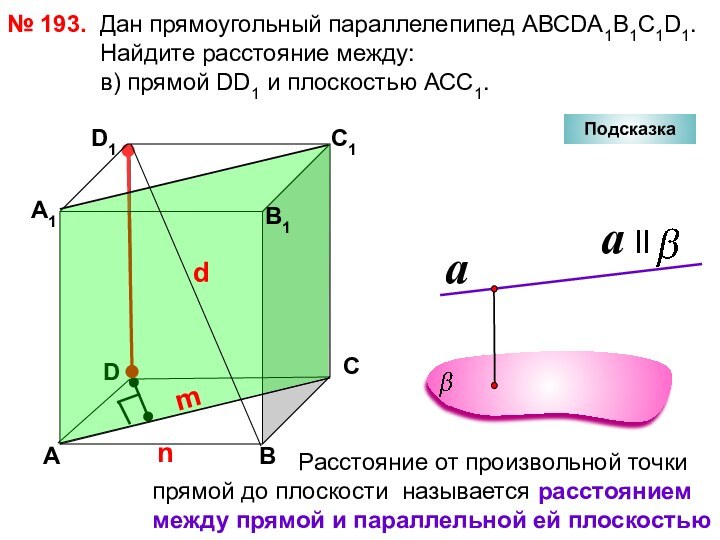
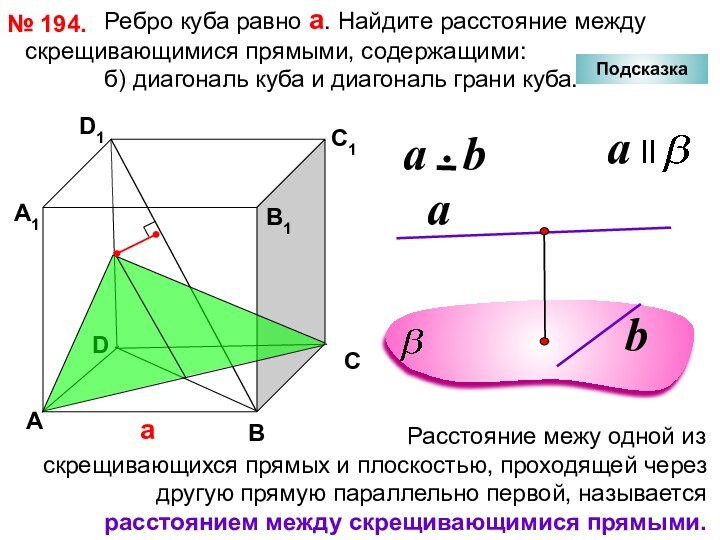
№ 194.
D
А
В
С
D1
С1
а
В1
А1
Подсказка
А
А1
С
В1
D
В
D1
С1
А
А1
В1
С