Презентация на тему поворот

О на кут називається перетворення фігури F

у фігуру F′, внаслідок якого кожна точка M фігури F переходить у точку M′ фігури F′ так, що ОM′=ОM і ∠MОM′= .

М

М′

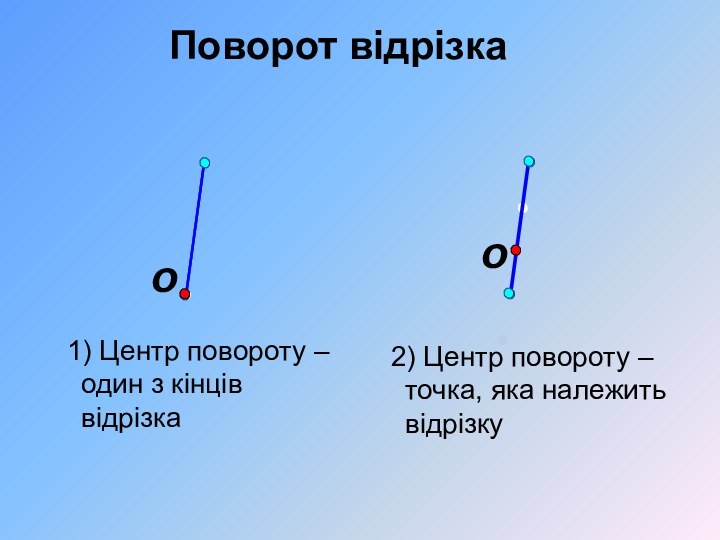
Точка О – центр повороту, – кут повороту.
Задається напрям – за годинниковою стрілкою або проти годинникової стрілки.

Означення

відрізка
2) Центр повороту – точка, яка належить відрізку

О на кут α

точку Х′, точка Y переходить у точку Y′.

Трикутники ХОY і Х′ОY′ рівні за І ознакою (ОХ=ОХ′, ОY =ОY′,
∠ХОY= ∠Х′ОY′). Отже, ХY =Х′Y′.

Х’

Y

Y’

Х

О

вершини на заданий кут.
Поворот многокутника

на кут α (0°< α ≤ 180°) фігура F

переходить у себе, то кажуть, що ця фігура має поворотну симетрію (або симетрію обертання).

щоб фігура відобразилась сама на себе?

є поворотом на 180°.
3) При повороті пряма переходить у

пряму;
кут – у рівний кут; відрізок – у рівний відрізок;
будь-яка фігура переходить у рівну їй фігуру.
4) Правильний трикутник під час повороту навколо центра трикутника на 120° переходить у себе.
Квадрат при повороті навколо центра квадрата на 90° (180°, 270°) переходить у себе.
Правильний шестикутник при повороті навколо свого центра на 60° (120°, 180°, 240°, 270°) переходить у себе.
Правильний многокутник при повороті навколо свого центра на кут переходить у себе.

у) при повороті на 90° відносно початку координат:
А) за

годинниковою стрілкою, то виконується умова: х1=-у,
у1=х;
Б) проти годинникової стрілки, то виконується умова: х1= у,
у1=-х.

Властивості повороту: