- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему по геометрии на тему Ромб
Содержание
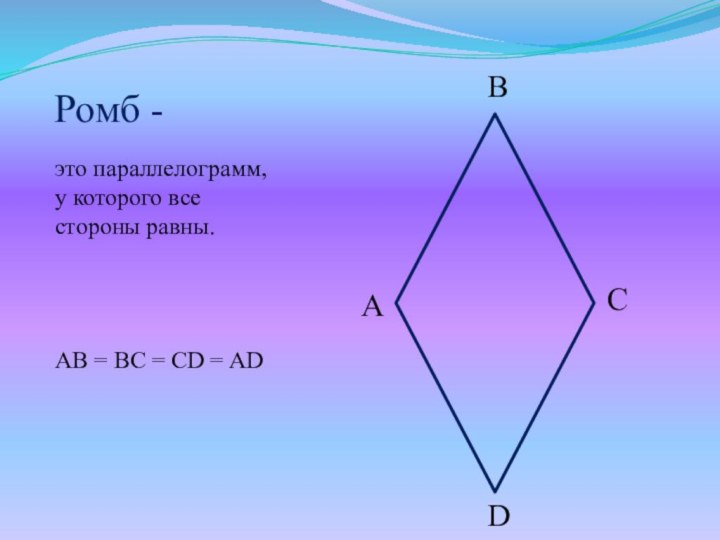
- 2. Ромб
- 3. Ромб - это параллелограмм, у которого все стороны равны.AB = BC = CD = ADABCD
- 4. Задачи для устного решенияДокажите, что параллелограмм ABCD – ромб.
- 5. ABCD
- 6. 302 см4 см
- 7. ABCD1234
- 8. Свойства ромба:Все свойства параллелограмма.Диагонали ромба взаимно перпендикулярны и являются биссектрисами его углов.
- 9. Диагонали ромба взаимно перпендикулярны и являются биссектрисами
- 10. Доказательство:Рассмотрим ΔABC :AB = BC =>
- 11. Задачи для устного решенияНайдите периметр ромба ABCD.
- 12. ABCD7 см
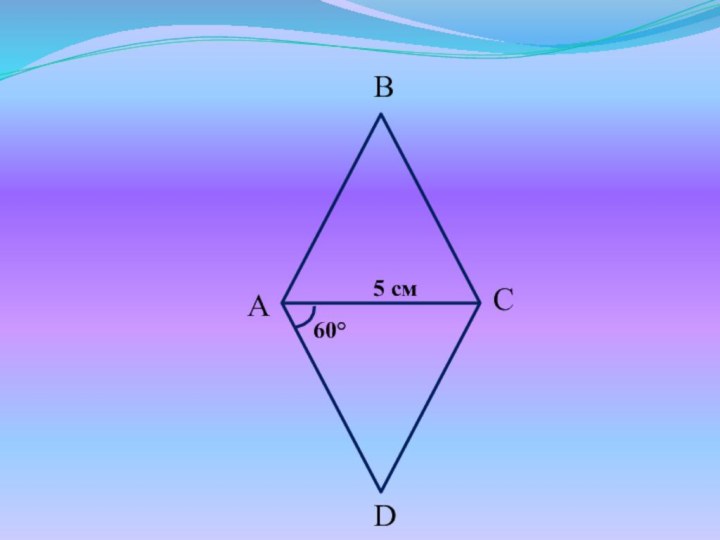
- 13. ABCD5 см60
- 14. ABCDEAE = 5 см
- 15. Признаки ромба:Если в четырехугольнике стороны равны, то
- 16. Задачи для устного решенияДокажите, что параллелограмм ABCD - ромб.
- 17. ABCD60
- 18. ABCD12
- 20. Задачи для самостоятельного решения
- 21. №1. Найти углы ромба, если его сторона образует с диагоналями углы, разность которых равна 20.
- 22. Дано:ABCD – ромб2 – 1 = 20 Найти:A -? B -?12
- 23. Решение:Т.к. ABCD – ромб, то ΔABO –
- 24. №2. Найти углы ромба, если его сторона образует с диагоналями углы, которые относятся как 2:7.
- 25. 12Дано:ABCD – ромб1 : 2 = 2 : 7 Найти:A -? B -?
- 26. Решение:Т.к. ABCD – ромб, то ΔABO –
- 27. №3. Высоты, проведенные из вершины тупого угла
- 28. Дано:ABCD –ромбBE AD BK CDEBK = 48 Найти:ABD - ? BAC - ?EK
- 29. Решение:Рассмотрим Δ ABE и ΔBCK – прямоуг.:
- 30. №4. На сторонах AB и AD ромба
- 31. Дано:ABCD – ромбAF = AEДоказать:FE AC
- 32. Решение:Δ AEF – равнобедренный (т.к. AE =
- 33. №5. Два равных ромба ABCD и OKPF
- 34. Дано:ABCD, OKPF – ромбыABCD = OKPFДоказать:OMCT - ромбMT
- 35. Доказательство:OK || FP || AB || DC,
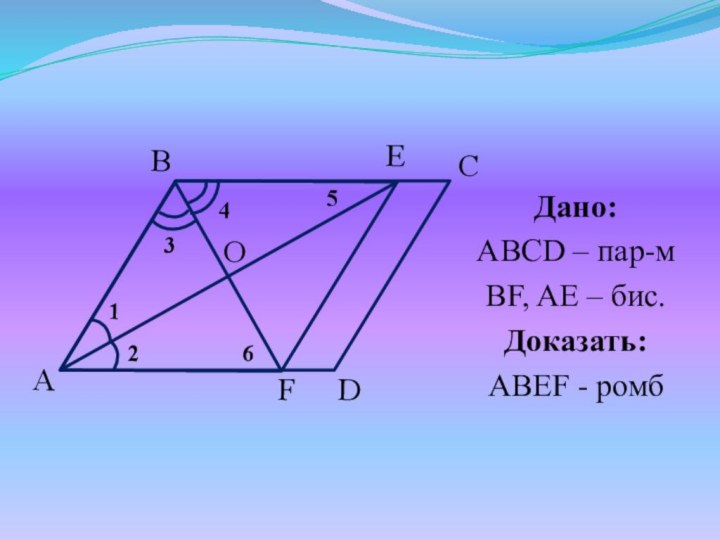
- 36. №6. В параллелограмме ABCD биссектрисы углов A
- 37. Дано:ABCD – пар-мBF, AE – бис.Доказать:ABEF - ромбEFO123465
- 38. Скачать презентацию
- 39. Похожие презентации
Ромб



































Слайд 8
Свойства ромба:
Все свойства параллелограмма.
Диагонали ромба взаимно перпендикулярны и
являются биссектрисами его углов.
Слайд 9 Диагонали ромба взаимно перпендикулярны и являются биссектрисами его
углов.
Дано:
ABCD – ромб
AC ∩ BD = O
Доказать:
AC BD
ABO
= CBOADO = CDO
BAO = DAO
BCO = DCO
A
B
C
D
O
Слайд 10
Доказательство:
Рассмотрим ΔABC :
AB = BC =>
ΔABC – равнобедренный
AC ∩ BD = O, AO =
OC => BO – медиана, высота, биссектриса.Получаем, что AC BD, ABO = CBO.
Аналогично получаем:
ADO = CDO
BAO = DAO
BCO = DCO
ч.т.д.
Слайд 15
Признаки ромба:
Если в четырехугольнике стороны равны, то этот
четырехугольник является ромбом.
Если в параллелограмме диагонали взаимно перпендикулярны, то
этот параллелограмм – ромб.Если в параллелограмме диагонали являются биссектрисами его углов, то этот параллелограмм – ромб.
Слайд 21 №1. Найти углы ромба, если его сторона образует
с диагоналями углы, разность которых равна 20.
Слайд 23
Решение:
Т.к. ABCD – ромб, то ΔABO – прямоуг.
2
- 1 = 20 => 2 = 1 +
20 Пусть 1 = x, тогда 2 = x + 20 1 + 2 = 90 (свойство углов прямоуг. Δ) x + x + 20 = 90 2x = 70 x = 351 = х = 35 , 2 = х + 20 = 55
Ответ: 35; 55.
Слайд 24 №2. Найти углы ромба, если его сторона образует
с диагоналями углы, которые относятся как 2:7.
Слайд 26
Решение:
Т.к. ABCD – ромб, то ΔABO – прямоуг.
1 + 2 = 90 (свойство углов прямоуг. Δ)
Пусть
х – коэффициент пропорциональности, тогда 1 = 2x, 2 = 7x 2x + 7x = 90 9x = 90 x = 10 1 = 2х = 20 , 2 = 7х = 70
A = 2 2 = 140, B = 2 1 = 40
Ответ: 40; 140.
Слайд 27 №3. Высоты, проведенные из вершины тупого угла ромба,
образуют угол в 48. Найти углы, образованные диагоналями ромба
с его сторонами.
Слайд 29
Решение:
Рассмотрим Δ ABE и ΔBCK – прямоуг.: A
= C AB = BC, а значит Δ ABE
= ΔBCK ( по гипотенузе и острому углу)Δ ABE = ΔBCK => BE = BK
Рассмотрим ΔBED и ΔDBK – прямоуг.: BE = BK BD – общая => ΔBED = ΔDBK (по гипотенузе и катету), а значит EBD = DBK = 48 : 2 = 24 => BDE = BDK = 90 - 24 = 66
AC BD (свойство ромба) => ΔABO = ΔADO (прямоуг.) BDE = 66 => OAD = OAB = 24
Ответ: 66; 24.
Слайд 30 №4. На сторонах AB и AD ромба ABCD
отложены равные отрезки AE и AF. Доказать, что EF
и AC перпендикулярны.
Слайд 32
Решение:
Δ AEF – равнобедренный (т.к. AE = AF)
AK – биссектриса A => AK – биссектриса, медиана и
высота, т.е. AK FEAK FE AK AC => FE AC
ч.т.д.
Слайд 33 №5. Два равных ромба ABCD и OKPF расположены
так, что точка пересечения диагоналей одного совпадает с вершиной
другого и наоборот. (см. рисунок) Определить вид четырехугольника OMCT.
Слайд 35
Доказательство:
OK || FP || AB || DC, OK
= FP = AB = DC AD || BC
|| OF || KP, AD = BC = OF = KP => OM || CT, MC || OT => OMCT – пар-м (по определению) Зн. OM = CT, MC = OT (свойство пар-ма)OM || AB, AO = OC => OM – средняя линия ΔABC Зн. OM = ½ AB = CT
OT || AD, AO = OC => OT – средняя линия ΔACD Зн. OT = ½ AD = MC
AB = AD => OM = MC = CT = OT = ½ AB
OMCT – пар-м OM = MC = CT = OT = ½ AB => OMCT – ромб (по определению)
ч.т.д.