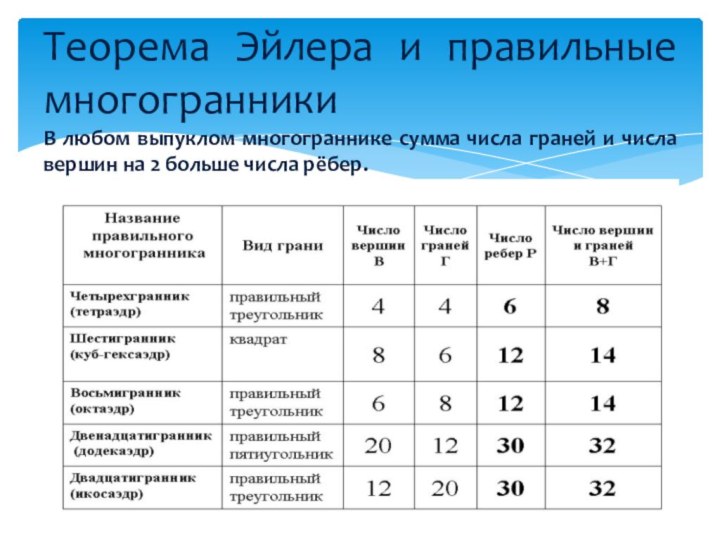
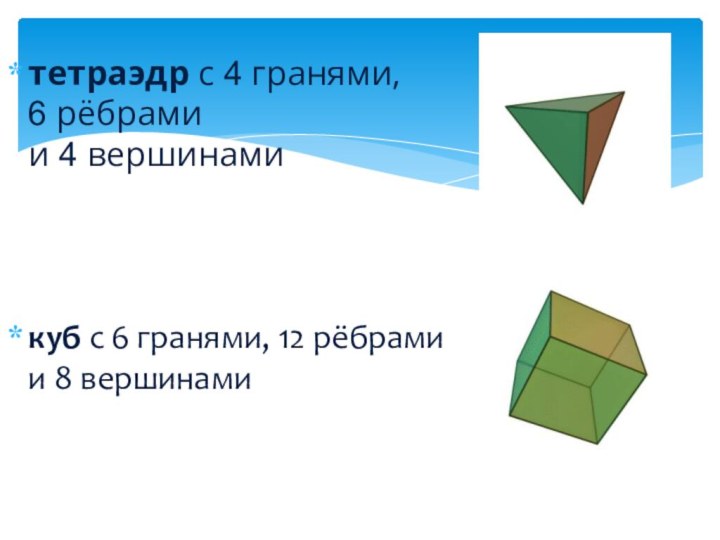
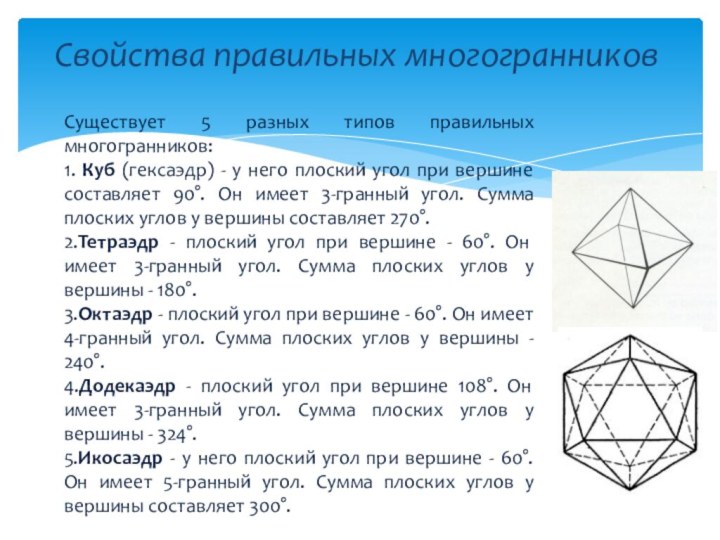
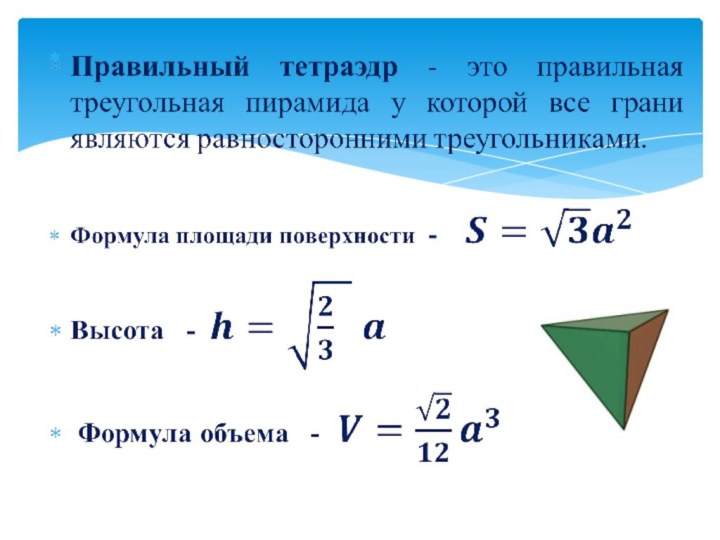
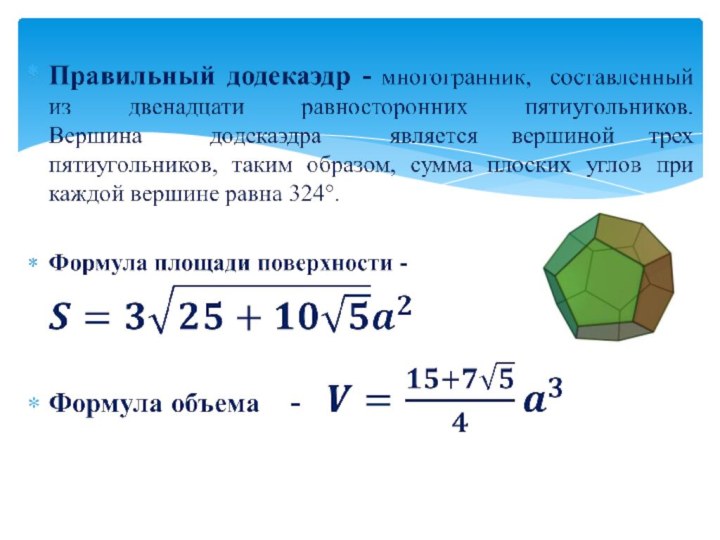
гранями являются правильные треугольники, правильные четырехугольники (квадраты) и правильные
пятиугольники.Правильным многогранником или Платоновым телом называется такой выпуклый многогранник, у которого все грани равны и представляют собой равные правильные многоугольники, все ребра также равны между собой.