Слайд 2
Итоговое повторение курса геометрии 7 класс
Презентация рассчитана на
2 урока
1 урок –повторение видов треугольников
Понятие медианы, высоты, биссектрисы
2урок-решение
задач на построение медиан, биссектрис и высот треугольников.
Решение задач на нахождение элементов треугольников.
Слайд 3
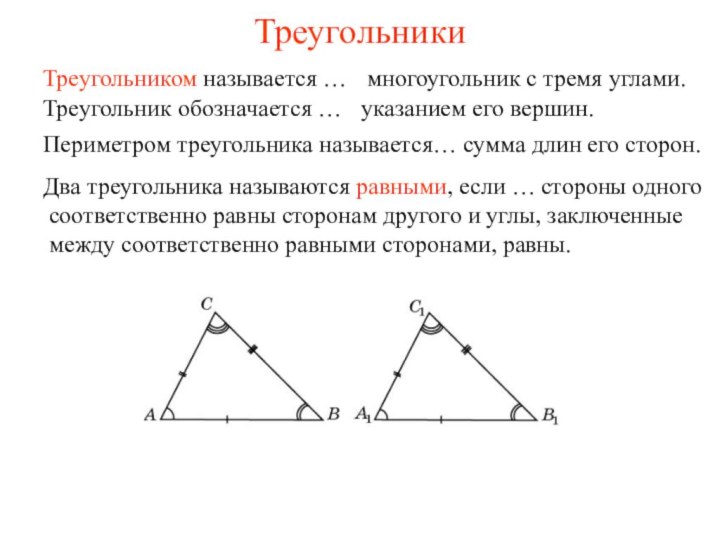
Треугольники
Треугольником называется …
многоугольник с тремя углами.
Треугольник
обозначается …
указанием его вершин.
стороны одного соответственно равны сторонам другого и углы, заключенные между соответственно равными сторонами, равны.
Периметром треугольника называется…
сумма длин его сторон.
Слайд 4
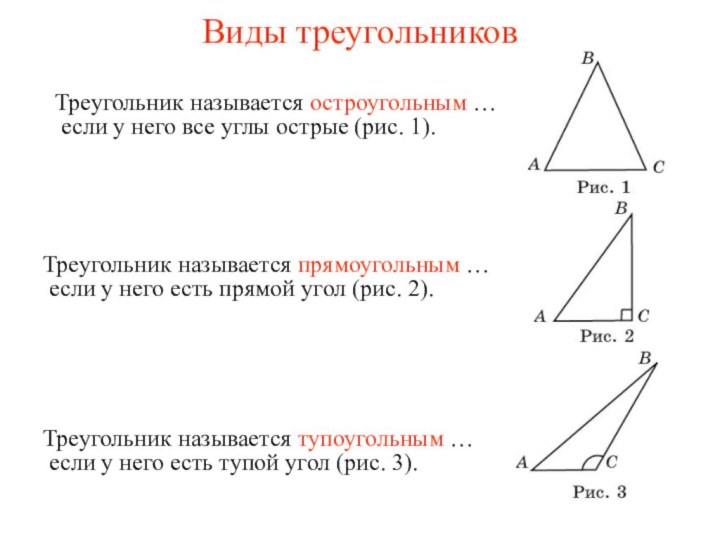
Виды треугольников
Треугольник называется остроугольным …
Треугольник называется прямоугольным …
Треугольник называется
тупоугольным …
Слайд 5
Элементы треугольника
Медиана треугольника –
Биссектриса треугольника –
Высота треугольника –
отрезок, соединяющий вершину треугольника с серединой противоположной стороны (рис. 1).
отрезок биссектрисы угла треугольника, соединяющий вершину с точкой противоположной стороны (рис. 2).
отрезок, соединяющий вершину треугольника с точкой противоположной стороны или ее продолжения и перпендикулярный этой стороне (рис. 3).
Слайд 6
Вопрос 1
Какая фигура называется треугольником?
Ответ: Треугольником называется
многоугольник с тремя углами.
Слайд 7
Вопрос 2
Как обозначается треугольник?
Ответ: Треугольник обозначается указанием его
вершин. Например, треугольник АВС.
Слайд 8
Вопрос 3
Что называется периметром треугольника?
Ответ: Периметром треугольника называется
сумма длин его сторон.
Слайд 9
Вопрос 4
Какой треугольник называется остроугольным?
Ответ: Остроугольным называется треугольник,
у которого все углы острые.
Слайд 10
Вопрос 5
Какой треугольник называется прямоугольным?
Ответ: Прямоугольным называется треугольник,
у которого имеется прямой угол.
Слайд 11
Вопрос 6
Какой треугольник называется тупоугольным?
Ответ: Тупоугольным называется треугольник,
у которого имеется тупой угол.
Слайд 12
Вопрос 7
Что называется медианой треугольника?
Ответ: Медиана треугольника –
отрезок, соединяющий вершину треугольника с серединой противоположной стороны.
Слайд 13
Вопрос 8
Что называется биссектрисой треугольника?
Ответ: Биссектриса треугольника –
отрезок биссектрисы угла треугольника, соединяющий вершину с точкой противоположной
стороны.
Слайд 14
Вопрос 9
Что называется высотой треугольника?
Ответ: Высота треугольника –
отрезок, соединяющий вершину треугольника с точкой противоположной стороны или
ее продолжения и перпендикулярный этой стороне.
Слайд 15
Вопрос 10
Какие треугольники называются равными?
Ответ: Два треугольника
называются равными, если стороны одного соответственно равны сторонам другого,
и углы, заключенные между соответственно равными сторонами, равны.
Слайд 16
Упражнение 1
Изобразите какой-нибудь остроугольный треугольник ABC, одной стороной
которого является отрезок AB, а вершина C находится в
одном из узлов сетки.
Слайд 17
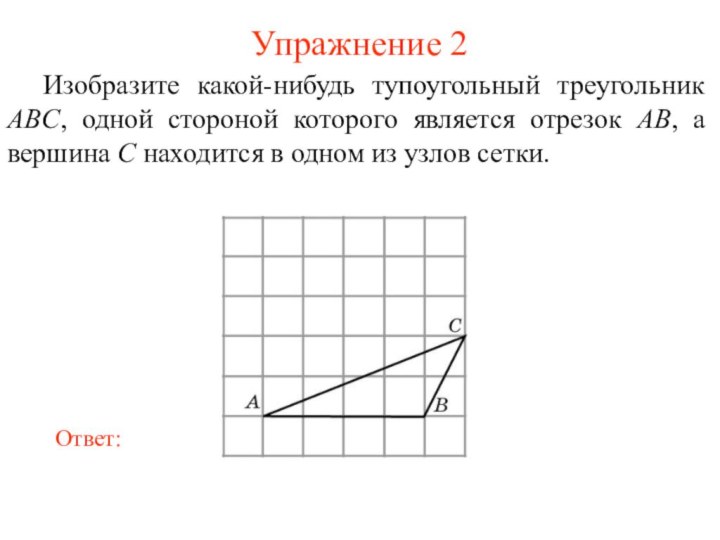
Упражнение 2
Изобразите какой-нибудь тупоугольный треугольник ABC, одной стороной
которого является отрезок AB, а вершина C находится в
одном из узлов сетки.
Слайд 18
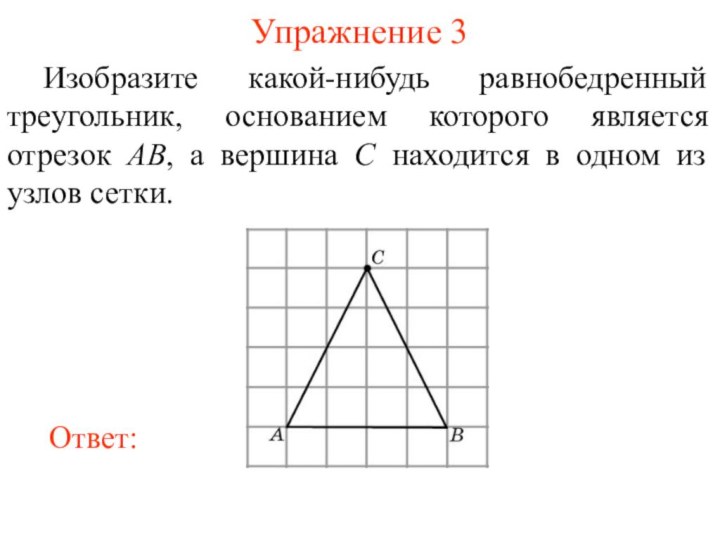
Упражнение 3
Изобразите какой-нибудь равнобедренный треугольник, основанием которого является
отрезок AB, а вершина C находится в одном из
узлов сетки.
Слайд 19
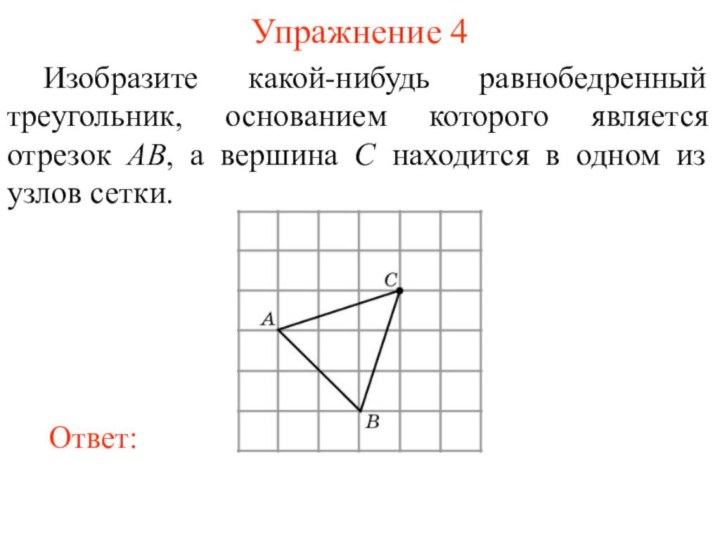
Упражнение 4
Изобразите какой-нибудь равнобедренный треугольник, основанием которого является
отрезок AB, а вершина C находится в одном из
узлов сетки.
Слайд 20
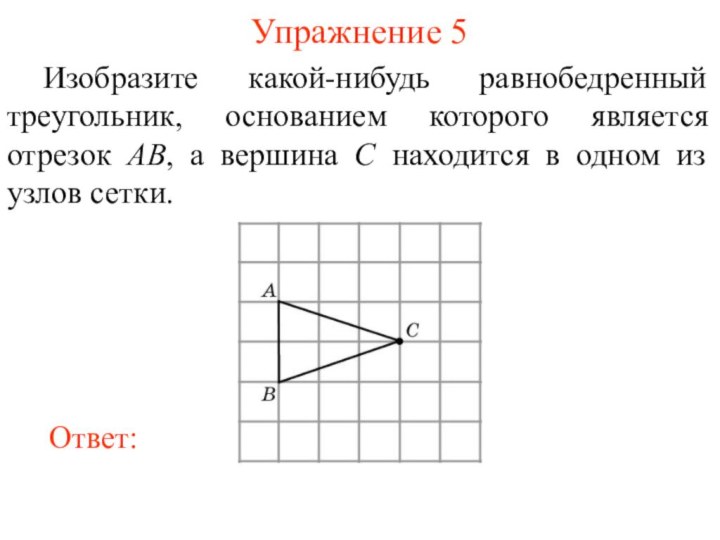
Упражнение 5
Изобразите какой-нибудь равнобедренный треугольник, основанием которого является
отрезок AB, а вершина C находится в одном из
узлов сетки.
Слайд 21
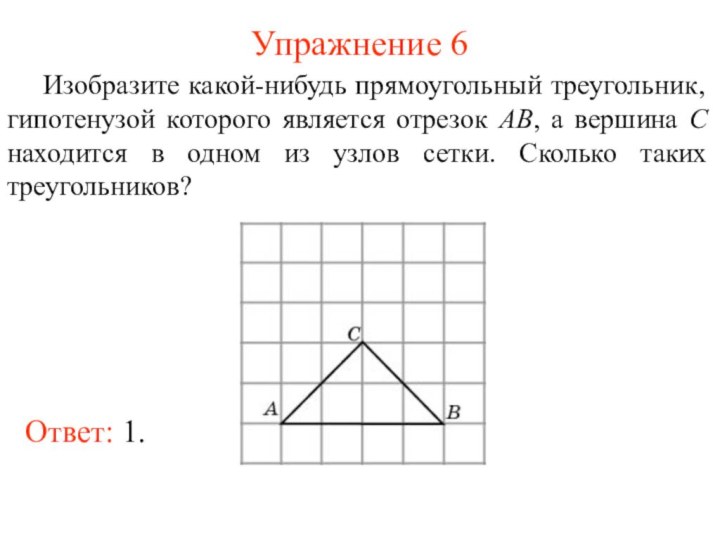
Упражнение 6
Изобразите какой-нибудь прямоугольный треугольник, гипотенузой которого является
отрезок AB, а вершина C находится в одном из
узлов сетки. Сколько таких треугольников?
Слайд 22
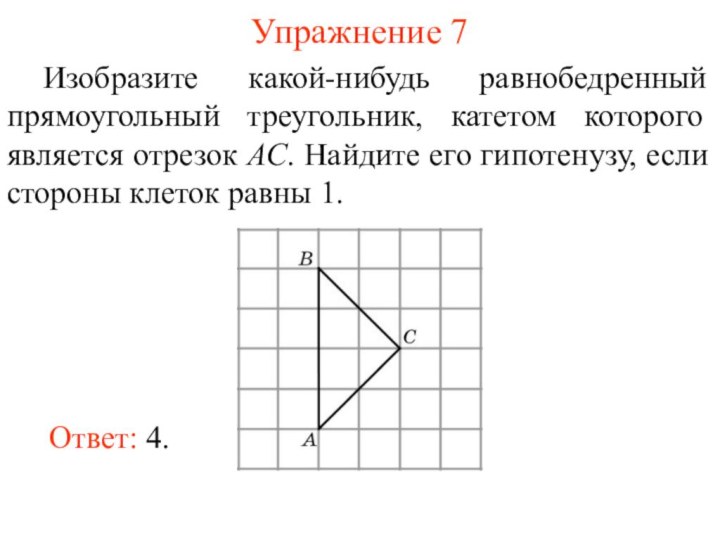
Упражнение 7
Изобразите какой-нибудь равнобедренный прямоугольный треугольник, катетом которого
является отрезок AC. Найдите его гипотенузу, если стороны клеток
равны 1.
Слайд 23
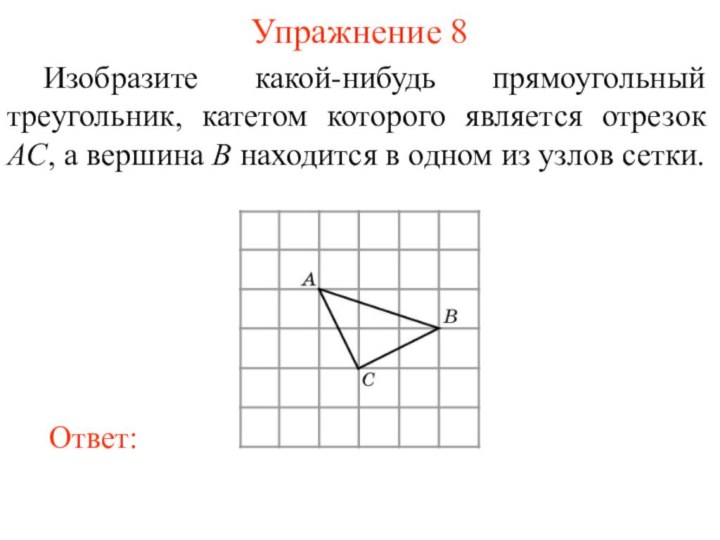
Упражнение 8
Изобразите какой-нибудь прямоугольный треугольник, катетом которого является
отрезок AC, а вершина B находится в одном из
узлов сетки.
Слайд 24
Упражнение 9
Изобразите какой-нибудь прямоугольный треугольник, гипотенузой которого является
отрезок AB, а вершина C находится в одном из
узлов сетки. Сколько таких треугольников?
Слайд 25
Упражнение 10
Изобразите какой-нибудь прямоугольный треугольник, гипотенузой которого является
отрезок AB, а вершина C находится в одном из
узлов сетки. Сколько таких треугольников?
Слайд 26
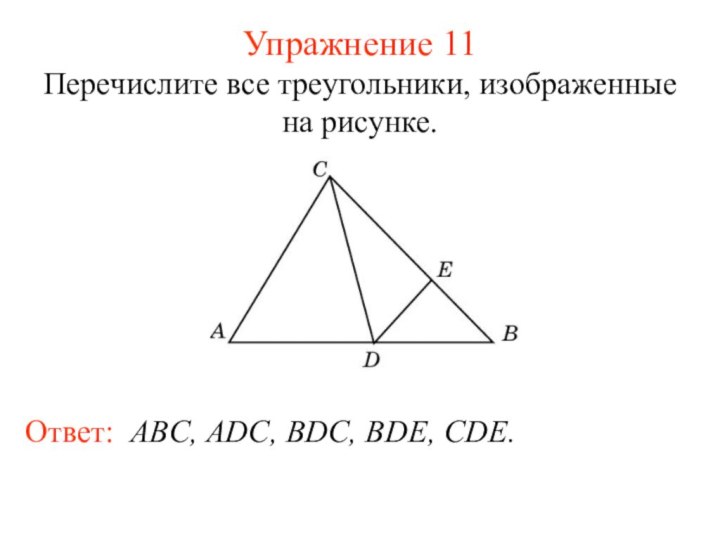
Упражнение 11
Перечислите все треугольники, изображенные на рисунке.
Ответ: ABC,
ADC, BDC, BDE, CDE.
Слайд 27
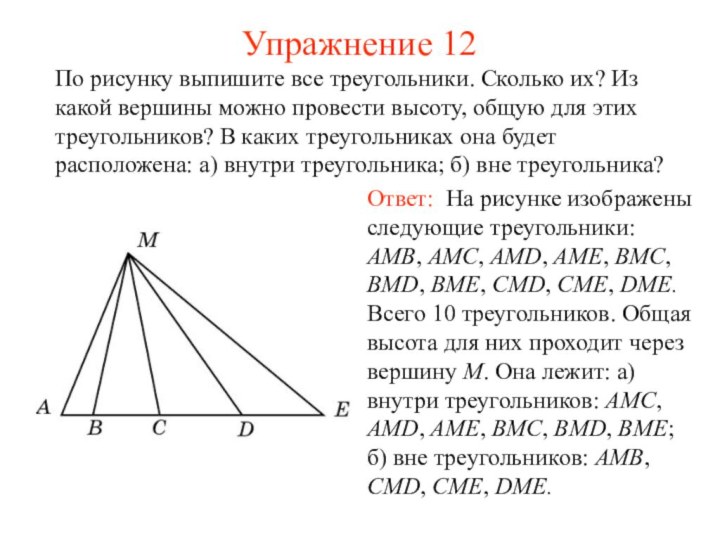
Упражнение 12
По рисунку выпишите все треугольники. Сколько их?
Из какой вершины можно провести высоту, общую для этих
треугольников? В каких треугольниках она будет расположена: а) внутри треугольника; б) вне треугольника?
Ответ: На рисунке изображены следующие треугольники: AMB, AMC, AMD, AME, BMC, BMD, BME, CMD, CME, DME. Всего 10 треугольников. Общая высота для них проходит через вершину M. Она лежит: а) внутри треугольников: AMC, AMD, AME, BMC, BMD, BME; б) вне треугольников: AMB, CMD, CME, DME.
Слайд 28
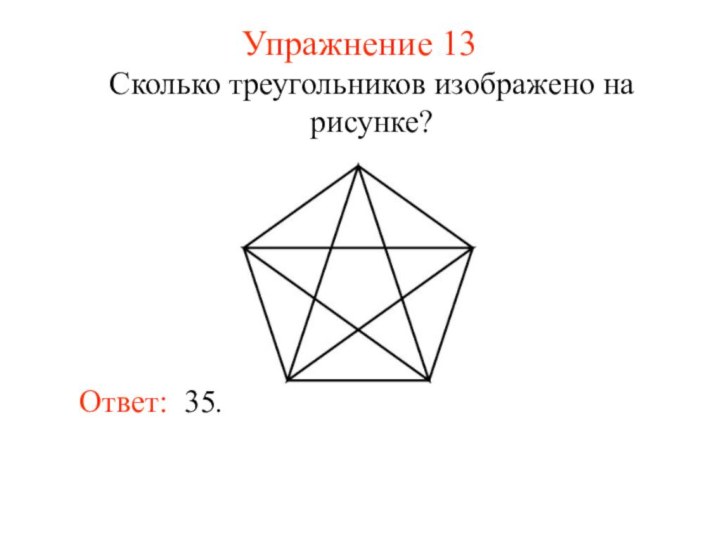
Упражнение 13
Сколько треугольников изображено на рисунке?
Ответ: 35.
Слайд 29
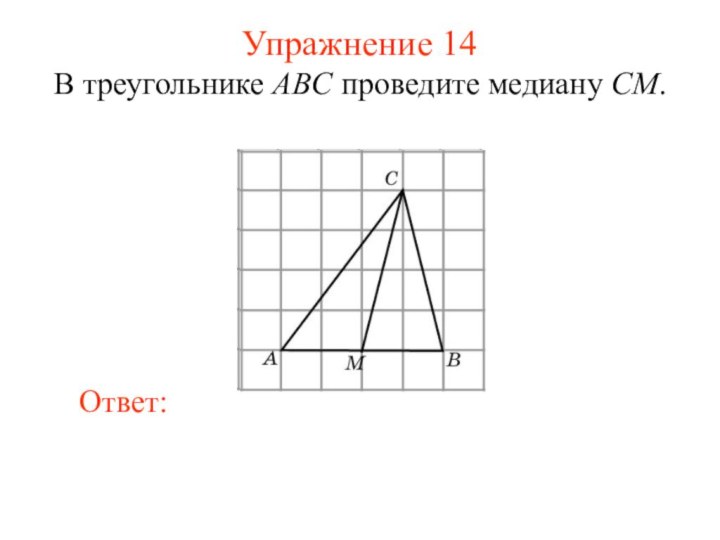
Упражнение 14
В треугольнике ABC проведите медиану CM.
Слайд 30
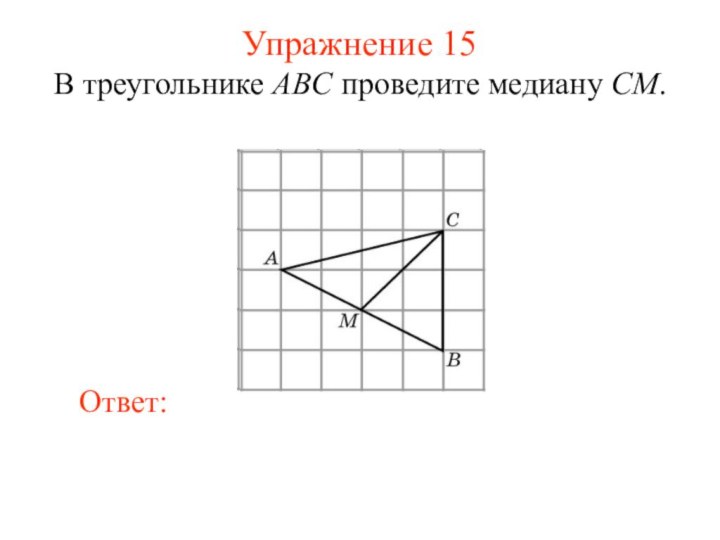
Упражнение 15
В треугольнике ABC проведите медиану CM.
Слайд 31
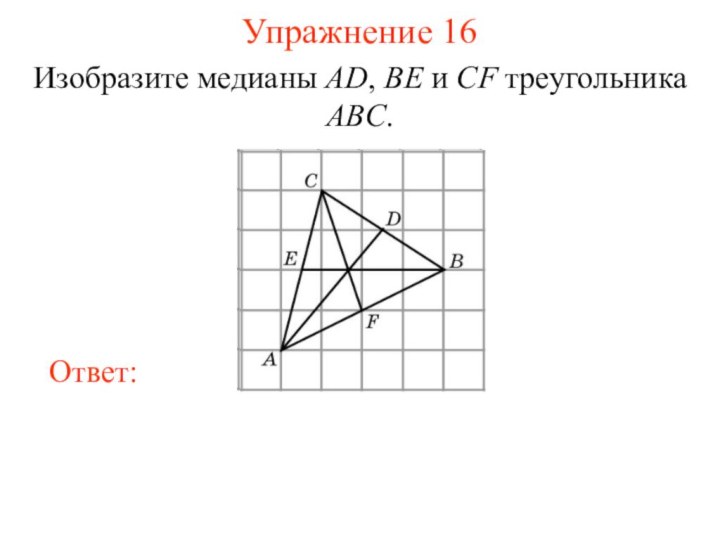
Упражнение 16
Изобразите медианы AD, BE и CF треугольника
ABC.
Слайд 32
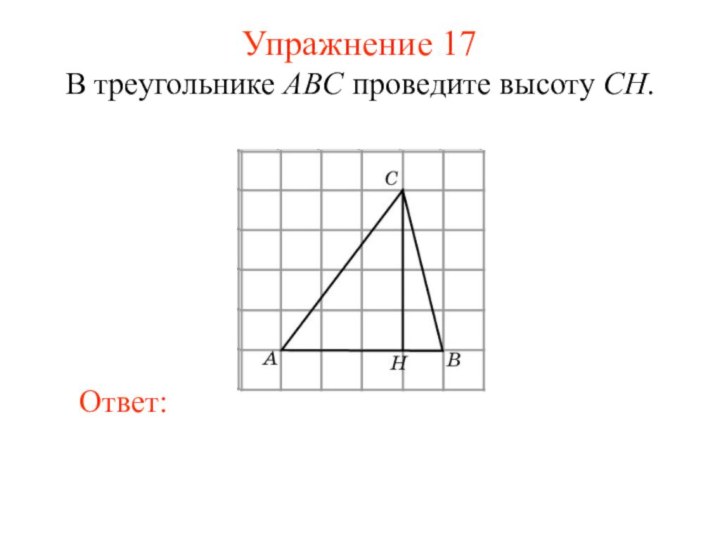
Упражнение 17
В треугольнике ABC проведите высоту CH.
Слайд 33
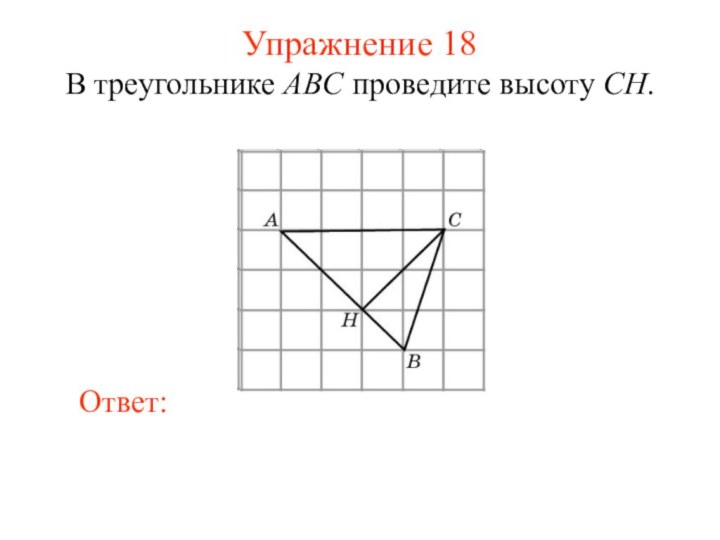
Упражнение 18
В треугольнике ABC проведите высоту CH.
Слайд 34
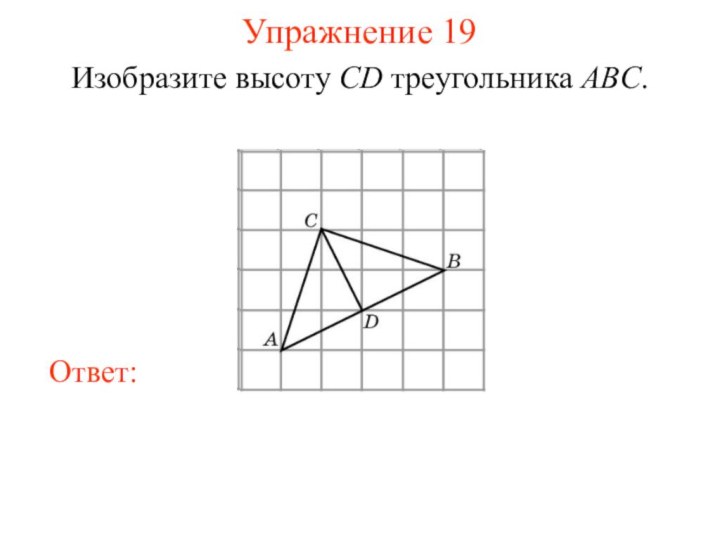
Упражнение 19
Изобразите высоту CD треугольника ABC.
Слайд 35
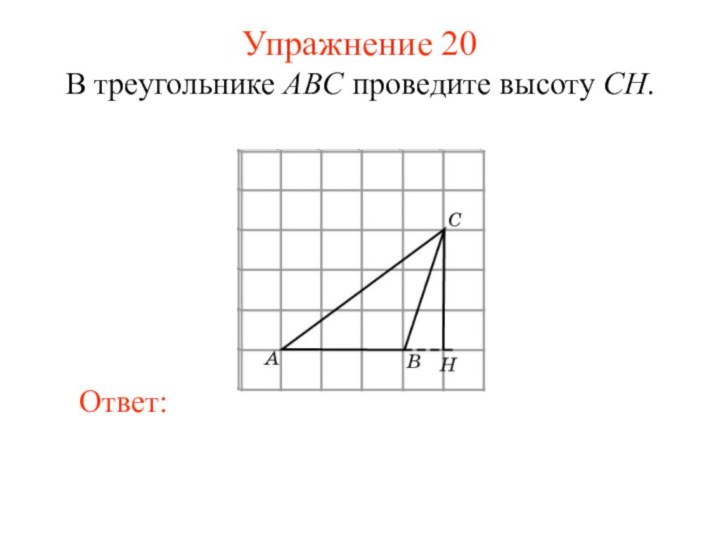
Упражнение 20
В треугольнике ABC проведите высоту CH.
Слайд 36
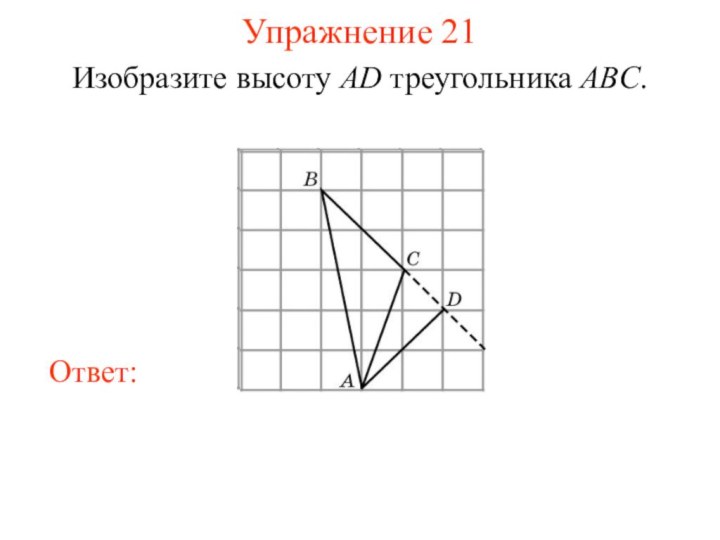
Упражнение 21
Изобразите высоту AD треугольника ABC.
Слайд 37
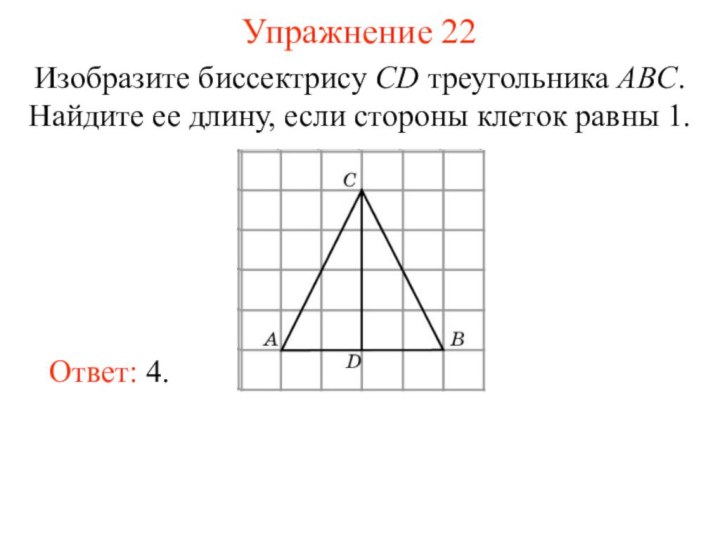
Упражнение 22
Изобразите биссектрису CD треугольника ABC. Найдите ее
длину, если стороны клеток равны 1.
Слайд 38
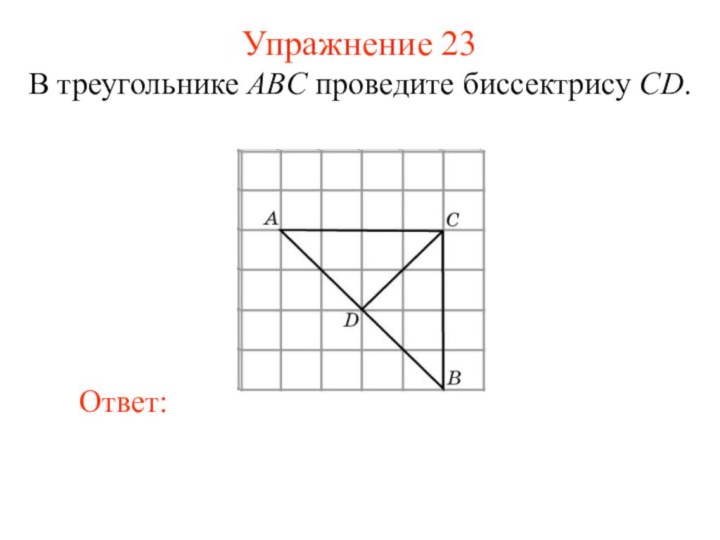
Упражнение 23
В треугольнике ABC проведите биссектрису CD.
Слайд 39
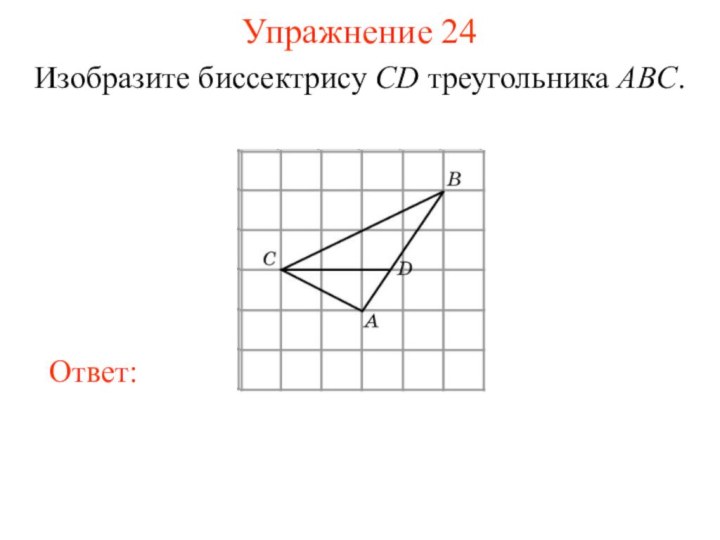
Упражнение 24
Изобразите биссектрису CD треугольника ABC.
Слайд 40
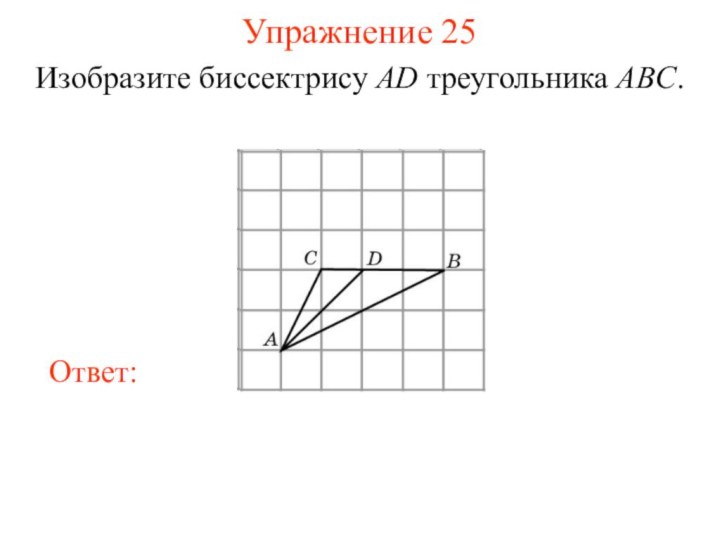
Упражнение 25
Изобразите биссектрису AD треугольника ABC.
Слайд 41
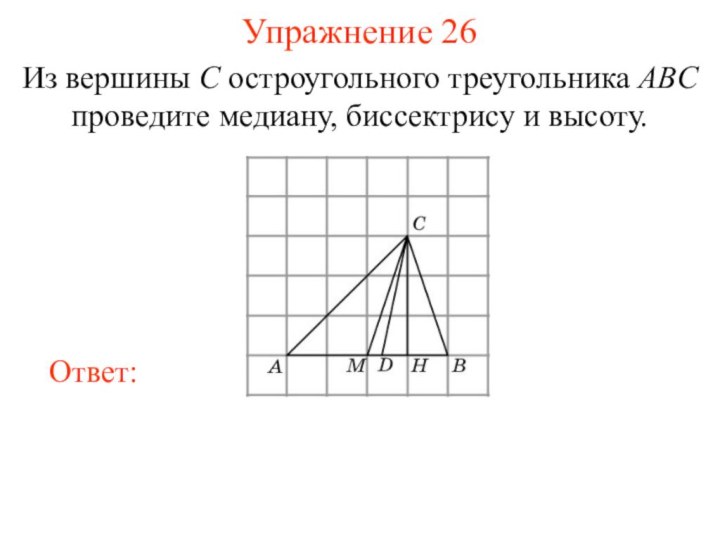
Упражнение 26
Из вершины C остроугольного треугольника ABC проведите
медиану, биссектрису и высоту.
Слайд 42
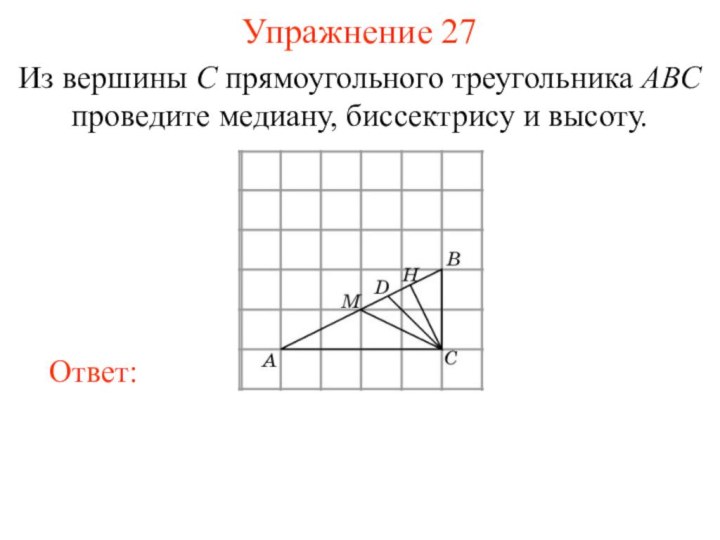
Упражнение 27
Из вершины C прямоугольного треугольника ABC проведите
медиану, биссектрису и высоту.
Слайд 43
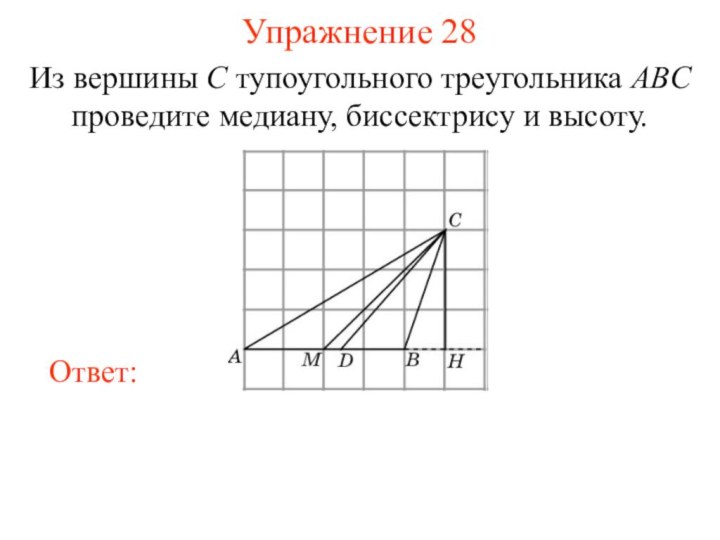
Упражнение 28
Из вершины C тупоугольного треугольника ABC проведите
медиану, биссектрису и высоту.
Слайд 44
Упражнение 29
Может ли проходить вне треугольника его: а)
медиана; б) биссектриса; в) высота?
Ответ: а), б) нет; в)
да.
Слайд 45
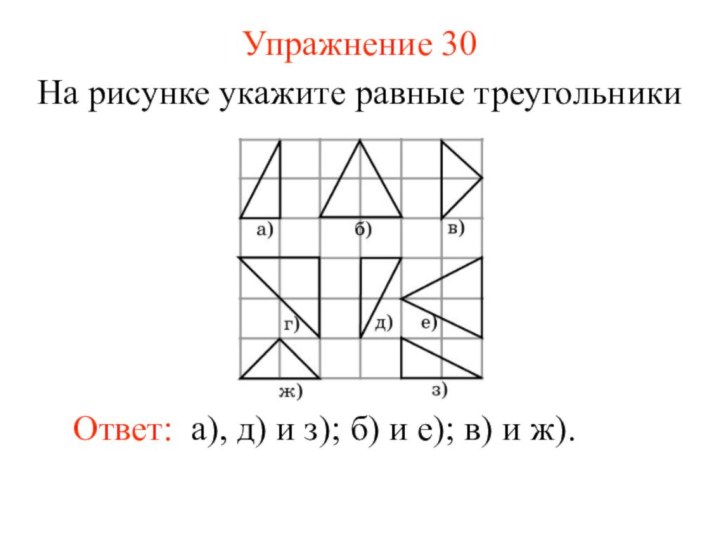
Упражнение 30
На рисунке укажите равные треугольники
Ответ: а), д)
и з); б) и е); в) и ж).
Слайд 46
Упражнение 31
Треугольники АВС и EFG равны. Известно, что
АВ = 5 см, ВС = 6 см, АС
= 7 см. Найдите стороны треугольника EFG.
Ответ: EF = 5 см, FG = 6 см, EG = 7 см.
Слайд 47
Упражнение 32
Треугольники АВС и EFG равны. Известно, что
А = 40o, В = 60o,
С = 80o. Найдите углы треугольника EFG.
Слайд 48
Упражнение 33
Треугольники АВС, PQR и XYZ равны. Известно,
что АВ = 5 см, QR = 6 см,
XZ = 7 см. Найдите остальные стороны каждого треугольника.
Ответ: BC = YZ = 6 см, AC = PR = 7 см, PQ = XY = 5 см.
Слайд 49
Упражнение 34
Периметр одного треугольника больше периметра другого. Могут
ли эти треугольники быть равными?
Ответ: Нет.
Слайд 50
Упражнение 35
Периметр треугольника равен 36 см. Его стороны
относятся как 2:3:4. Найдите его стороны.
Ответ: 8 см,
12 см, 16 см.
Слайд 51
Упражнение 36
Периметр треугольника равен 48 см. Одна из
его сторон 18 см. Найдите две другие стороны, если
их разность равна 4 см.
Ответ: 13 см, 17 см.
Слайд 52
Упражнение 37
Периметр треугольника равен 35 см. Первая из
его сторон больше второй на 2 см, а третья
меньше второй на 3 см. Найдите стороны треугольника.
Ответ: 9 см, 12 см, 14 см.