Слайд 2
Историческая справка
Для первобытных людей важную роль играла
форма окружающих их предметов. По форме и цвету они
отличали съедобные грибы от несъедобных, пригодные для построек деревья и деревья, которые годятся лишь на дрова, вкусные орехи от горьких или ядовитых. Особенно вкусны орехи кокосовой пальмы. Эти орехи очень похожи на шар.
А добывая каменную соль или горный кварц, люди наталкивались на кристаллы, потом научились шлифовать их. Отшлифованные орудия позволили быстро срубить дерево, разрезать мясо, помогали лучше охотиться на зверей. Специальных названий для геометрических фигур тогда не было. Говорили: "Такой, как кокосовый орех”, (т. е. круглый), "такой, как соль” (т. е. имеющий форму куба). Некоторые формы фигур казались особо красивыми. И действительно, нельзя без восхищения смотреть на красоту кристаллов, цветов, фигур, имеющих правильную круглую форму.
Слайд 3
Историческая справка
Только в Древней Греции окружность и
круг получили свои названия.
Круглые тела в древности заинтересовали человека.
Так в Древнем Египте для постройки знаменитых египетских пирамид никаких технических сооружений еще не было. Даже шлифовать огромные каменные глыбы приходилось вручную, а перемещали их с помощью бревен круглой формы. Позже вместо бревен стали использовать их части – в виде колес, которые катились уже легче.
Слайд 4
Историческая справка
А теперь давайте поразмышляем о колесе.
В
Древней Греции круг и окружность считали венцом совершенства. В
каждой своей точке окружность устроена одинаковым образом, что позволяет ей двигаться самой по себе. Это свойство окружности стало толчком к возникновению колеса, так как ось и втулка колеса должны всё время быть в соприкосновении. К сожалению, неизвестен изобретатель колеса. Колесо – это чудо! Что же в нём особенного? – подумаете вы. Но это только на первый взгляд. Представьте себе на секунду, что вдруг случилась беда: на Земле исчезли все колёса!
Слайд 5
Основные понятия
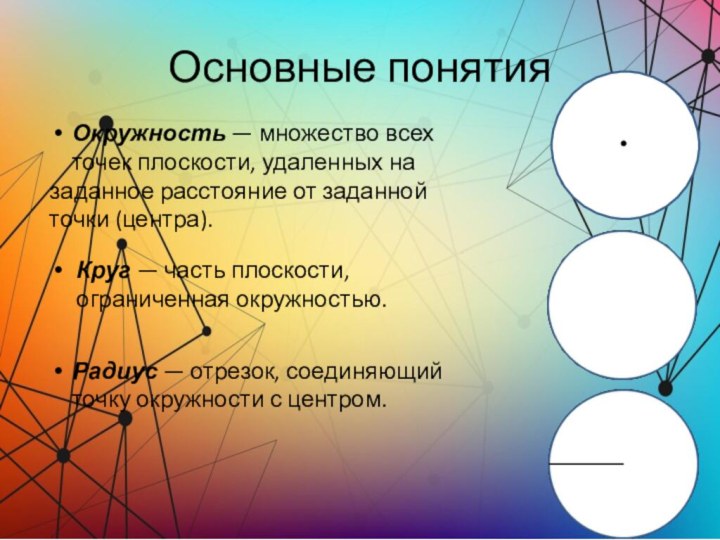
Окружность — множество всех точек плоскости,
удаленных на
заданное расстояние от заданной точки (центра).
Круг — часть
плоскости, ограниченная окружностью.
Радиус — отрезок, соединяющий точку окружности с центром.
Слайд 6
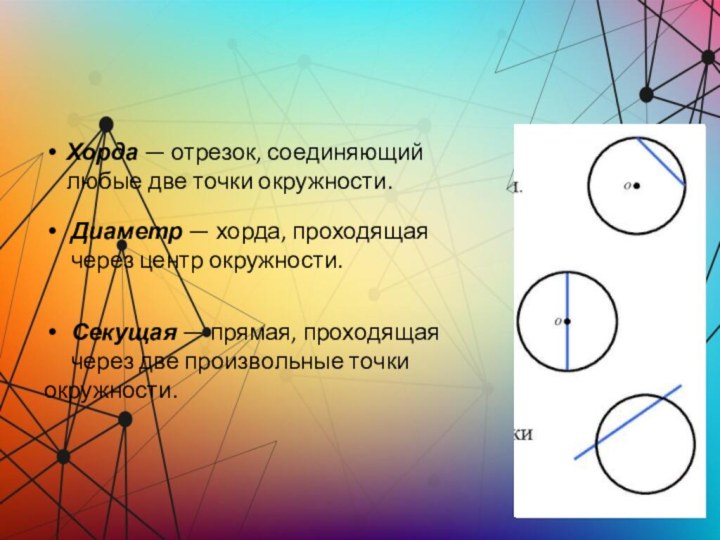
Хорда — отрезок, соединяющий любые две точки окружности.
Диаметр
— хорда, проходящая через центр окружности.
Секущая — прямая, проходящая
через две произвольные точки
окружности.
Слайд 7
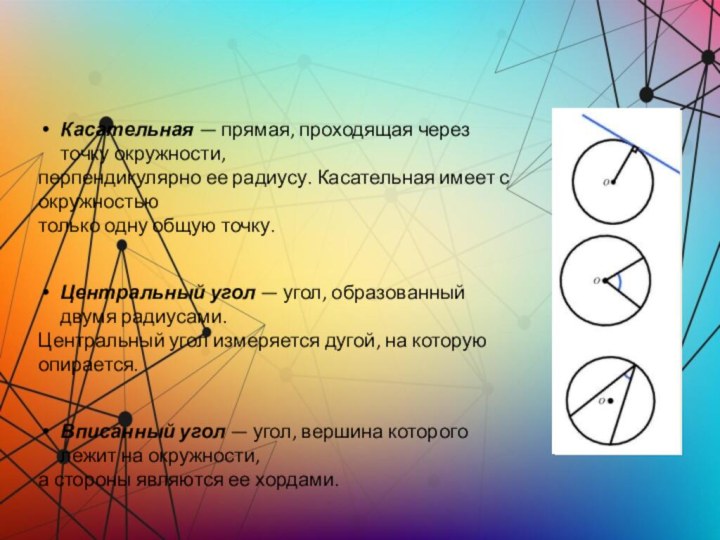
Касательная — прямая, проходящая через точку окружности,
перпендикулярно ее
радиусу. Касательная имеет с окружностью
только одну общую точку.
Центральный угол
— угол, образованный двумя радиусами.
Центральный угол измеряется дугой, на которую опирается.
Вписанный угол — угол, вершина которого лежит на окружности,
а стороны являются ее хордами.
Слайд 8
Теория
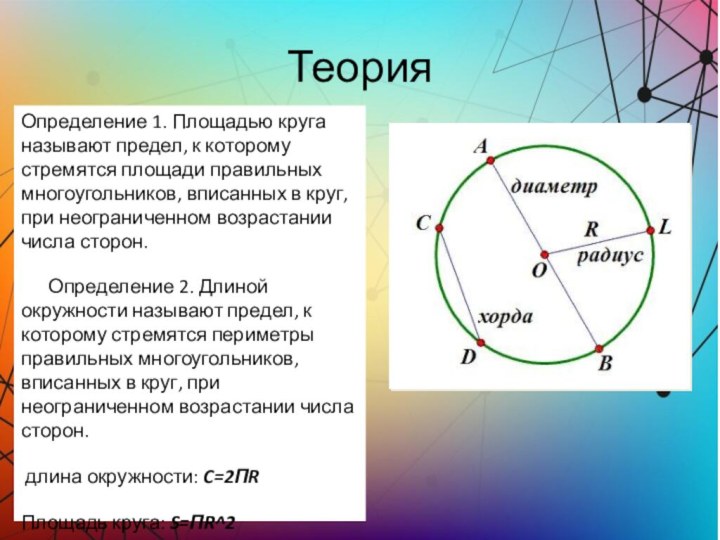
Определение 1. Площадью круга называют предел, к
которому стремятся площади правильных многоугольников, вписанных в круг, при
неограниченном возрастании числа сторон.
Определение 2. Длиной окружности называют предел, к которому стремятся периметры правильных многоугольников, вписанных в круг, при неограниченном возрастании числа сторон.
длина окружности: C=2ПR
Площадь круга: S=ПR^2
Слайд 9
Теория
Замечание 1. Доказательство того, что пределы площадей
и периметров правильных многоугольников, вписанных в круг, при неограниченном
возрастании числа сторон действительно существуют, выходит за рамки школьной математики и в нашем справочнике не приводится.
Определение 3. Числом π (пи) называют число, равное площади круга радиуса 1.
Замечание 2. Число π является иррациональным числом, т.е. числом, которое выражается бесконечной непериодической десятичной дробью: 3,1415…
Число π является трансцендентным числом, то есть числом, которое не может быть корнем алгебраического уравнения с целочисленными коэффициентами.
Слайд 11
Задачи
1.Корова привязана цепью длиной 5,4 м. Какая
площадь доступна ей?
2. Вычисли радиус круга, если его площадь
S=4πм2
3. Вырази из формулы длины окружности C=2 π R
число2 =?
Слайд 12
Решение
1. S=πR2. S=29,16π2
2.Площадь круга вычисляется по формуле:
S=πR2.
πR2=4π
| :π
R2=4
R=4√
R=2 м
3. число2= C/πR
Слайд 13
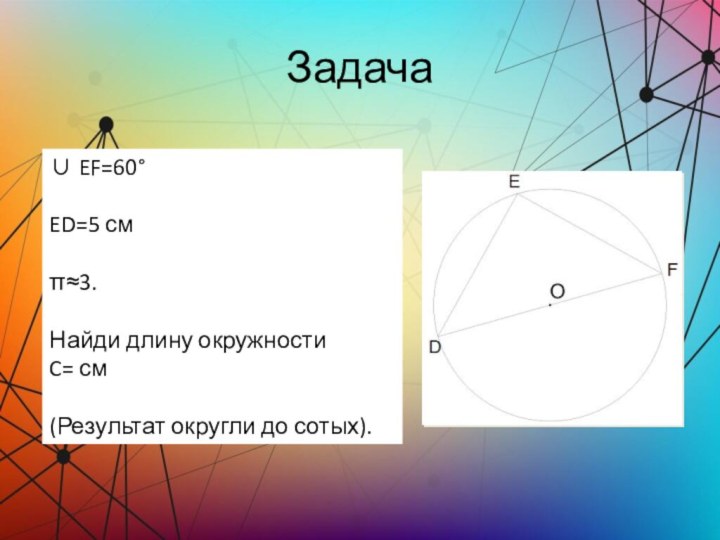
Задача
∪ EF=60°
ED=5 см
π≈3.
Найди длину окружности
C=
см
(Результат округли до сотых).
Слайд 14
Решение
1. ∢D=0,5∪EF=30° (по свойству вписанного угла)
2.
∢Е=90° (т.к. опирается на диаметр)
cosD=прилежащий катет/гипотенуза=ED/DF
cos30 °=3/√2
3/√2=5/DF
3√DF=2⋅5
DF=10/√3 (умножаем на √3, чтобы избавиться от иррациональности в знаменателе)
DF=10⋅√3/3 см
2R=DF=10⋅√3/3 см
3.C=2Rπ
C=10⋅√3/3π см
4. Подставляем π≈3
C=(10⋅√3/3)⋅3
C=10⋅3√
C=17,32 см
Слайд 15
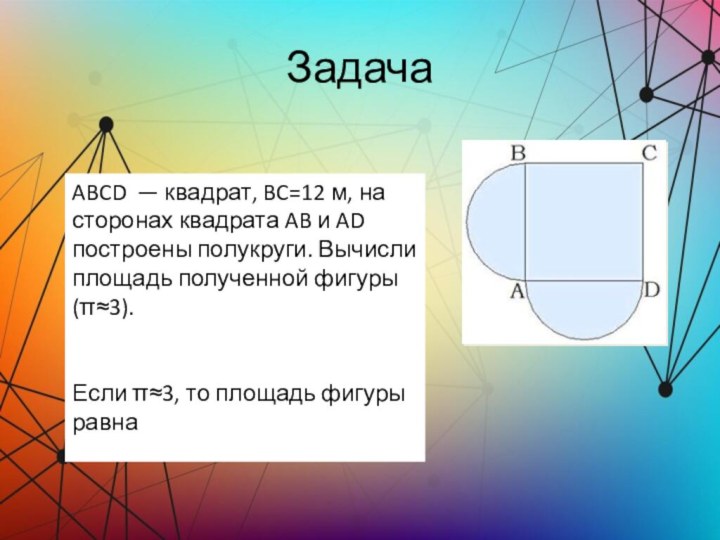
Задача
ABCD — квадрат, BC=12 м, на сторонах
квадрата AB и AD построены полукруги. Вычисли площадь полученной
фигуры (π≈3).
Если π≈3, то площадь фигуры равна
Слайд 16
Решение
Оба полукруга вместе образуют целый круг.
S=S(квадрата)+S(круга)
Радиус
круга R=BC/2=12/2=6 м
S(квадрата)= BC2=144м2
S(круга)=πR2=π⋅62=36π если
π≈3,то S(круга)=108м2
S=144+108=252м2
Слайд 17
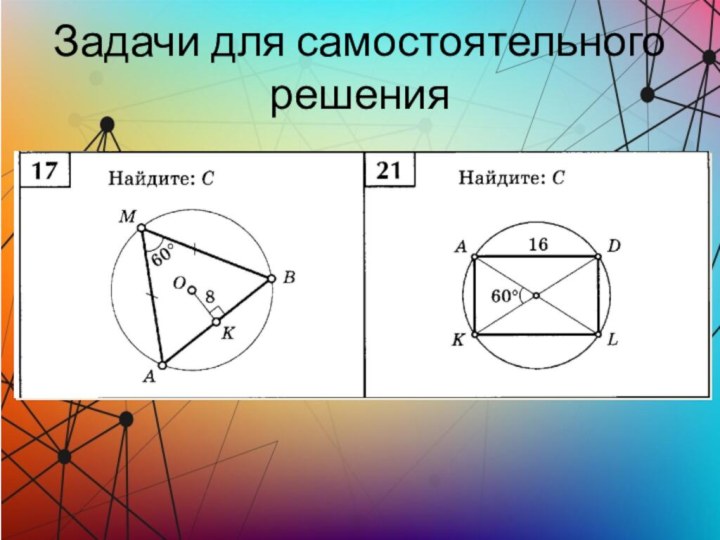
Задачи для самостоятельного решения
Слайд 18
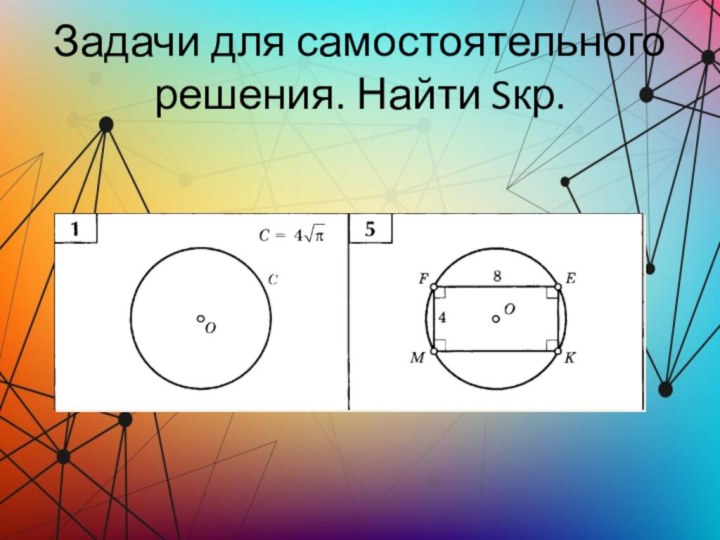
Задачи для самостоятельного решения. Найти Sкр.